目录
引言
一、算法概述
二、算法步骤
1 初始化
2 循环处理
三、算法应用
1 图的最短路径问题
2 网络爬虫
3 社交网络分析
4 游戏路径搜索
事例
四、算法特点与性能
五、性能优化
1 剪枝策略:
2 使用高效的数据结构:
3 并行化处理:
4 启发式搜索:
5 减少重复计算:
6 图压缩与稀疏性处理:
7 优化队列操作:
六、总结
引言
广度优先算法(Breadth-First Search,简称BFS)是一种用于遍历或搜索树或图的算法。它按照树的层次,或者图的层级,逐层访问节点。这种算法首先访问起始节点,然后遍历起始节点的所有邻居节点,接着再遍历这些邻居节点的未被访问过的邻居节点,如此逐层扩展,直到所有可达的节点都被访问过。
一、算法概述
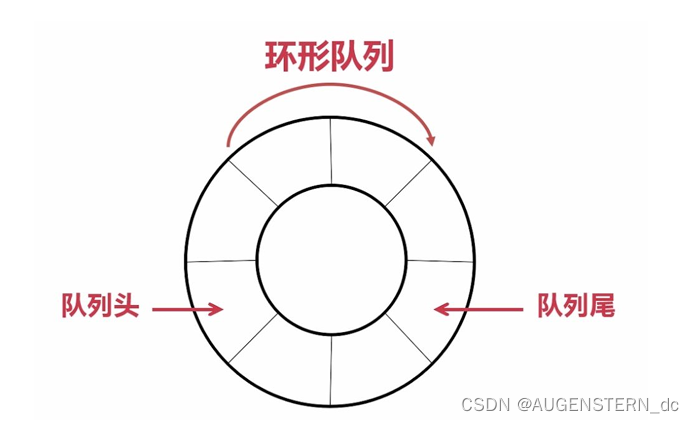
广度优先算法的主要特点是从起始节点开始,逐层向外扩展,直到遍历完所有可达的节点。在遍历过程中,它使用一种称为队列的数据结构来保存待访问的节点。队列是一种先进先出(FIFO)的数据结构,非常适合用来实现广度优先搜索。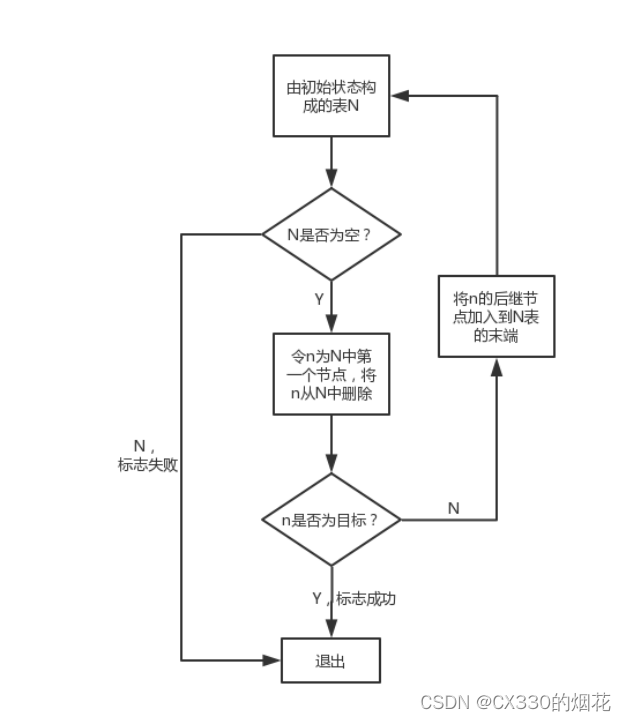
二、算法步骤
广度优先算法的基本步骤如下:
1 初始化
创建一个队列Q,并将起始节点s放入队列中。同时,创建一个集合visited,用于记录已经访问过的节点,初始时将起始节点s加入visited。
2 循环处理
当队列Q不为空时,执行以下步骤:
- 从队列Q中取出一个节点n。
- 遍历节点n的所有邻居节点m。对于每一个未被访问过的邻居节点m,执行以下操作:将节点m加入队列Q,并将节点m加入visited集合。
- 结束:当队列Q为空时,表示所有可达的节点都已经被访问过,算法结束。
三、算法应用
广度优先算法在许多领域都有广泛的应用,包括但不限于:
1 图的最短路径问题
广度优先算法可以用于寻找无向图或有向图中从起始节点到目标节点的最短路径。这是因为它总是先访问离起始节点最近的节点。
2 网络爬虫
在网页抓取和搜索引擎中,广度优先算法可以用来按照网页的链接关系,逐层抓取网页信息。
3 社交网络分析
在社交网络中,广度优先算法可以用来分析用户的社交关系,找出用户的朋友、朋友的朋友等。
4 游戏路径搜索
在一些游戏(如迷宫游戏)中,广度优先算法可以用来搜索从起点到终点的最短路径。
事例
以下是使用Python编写的广度优先搜索(BFS)算法的基本实现。这个代码示例假设我们有一个图,表示为邻接列表,并从一个指定的起始节点开始搜索。
from collections import deque
def bfs(graph, root):
visited = set()
queue = deque([root])
while queue:
vertex = queue.popleft()
print(vertex, end=" ")
for neighbour in graph[vertex]:
if neighbour not in visited:
visited.add(neighbour)
queue.append(neighbour)
# 示例图的邻接列表表示
graph = {
'A' : ['B','C'],
'B' : ['D', 'E'],
'C' : ['F'],
'D' : [],
'E' : ['F'],
'F' : []
}
bfs(graph, 'A') # 从节点'A'开始广度优先搜索
在这个代码中,我们首先创建了一个集合visited来跟踪已经访问过的节点,以及一个双端队列queue来保存待访问的节点。然后,我们进入一个循环,只要队列不为空,我们就从队列的左侧取出一个节点,并打印它。然后,我们遍历该节点的所有邻居,如果邻居尚未被访问过,我们就将其添加到visited集合和queue中。
这个简单的实现假设图是连通的,也就是说从起始节点可以到达图中的所有其他节点。如果图不是连通的,你可能需要修改代码以处理多个起始节点,或者遍历图中的每个节点以作为起始节点。
注意:在实际应用中,你可能需要根据你的具体需求对代码进行修改或扩展,例如添加错误处理、处理有向图或无向图、处理带权图等。
四、算法特点与性能
广度优先算法的主要特点在于它按照层次进行搜索,总是先访问离起始节点近的节点。这种特性使得它在某些问题(如最短路径问题)上具有很高的效率。然而,它也有其局限性,比如在搜索空间非常大或者图不是完全连通的情况下,可能会消耗大量的时间和内存。
从性能角度来看,广度优先算法的时间复杂度主要取决于图中节点的数量和边的数量。在最坏情况下,它需要访问图中的所有节点和边,因此时间复杂度为O(V+E),其中V是节点数,E是边数。空间复杂度方面,由于需要使用队列来保存待访问的节点,因此空间复杂度至少为O(V),在最坏情况下可能达到O(V+E)。
五、性能优化
优化广度优先算法(BFS)的性能主要涉及到减少不必要的搜索、提高数据结构的效率以及并行化处理等方面。以下是一些建议:
1 剪枝策略:
在搜索过程中,如果发现某个节点不满足特定条件或已经确定不可能达到目标,可以立即停止对该节点的进一步搜索,即“剪枝”。这可以有效减少搜索空间,提高算法效率。
2 使用高效的数据结构:
选择合适的数据结构来存储队列和已访问节点集合,以提高访问和插入操作的效率。例如,可以使用双端队列(deque)作为队列,以便在必要时从队列两端进行插入和删除操作。
对于大规模图数据,可以考虑使用哈希表或其他高效的数据结构来存储节点的邻接关系,以便快速查找节点的邻居。
3 并行化处理:
如果硬件条件允许,可以尝试将广度优先搜索算法并行化。通过将搜索任务分配给多个处理器或线程,可以显著提高算法的执行速度。
并行化时需要注意数据同步和通信开销,以确保并行化的效果是积极的。
4 启发式搜索:
在某些情况下,可以结合启发式信息来指导搜索过程。例如,在寻找最短路径时,可以使用启发式函数来估计从当前节点到目标节点的距离,从而优先搜索更有可能到达目标的节点。
5 减少重复计算:
在某些应用中,可能需要多次执行广度优先搜索。在这种情况下,可以考虑使用缓存或其他机制来存储已经计算过的结果,以避免重复计算。
6 图压缩与稀疏性处理:
对于稀疏图(即边数远小于节点数平方的图),可以使用压缩稀疏行(CSR)或压缩稀疏列(CSC)等格式来存储图数据,以减少内存占用并提高访问速度。
对于大规模图数据,可以考虑使用图划分或图嵌入等技术来降低图的复杂度,从而提高搜索效率。
7 优化队列操作:
在实现广度优先搜索时,优化队列的入队和出队操作也是提高性能的关键。例如,可以使用循环队列来避免队列的扩容和缩容操作,从而提高效率。
请注意,不同的应用场景和数据特点可能需要采用不同的优化策略。因此,在实际应用中,需要根据具体情况选择合适的优化方法,并进行充分的测试和验证。
六、总结
广度优先算法是一种强大而有效的图遍历算法,它通过逐层扩展的方式搜索图中的节点。虽然它在某些情况下可能会受到性能限制,但它在许多实际应用中仍然发挥着重要作用。无论是网络爬虫、社交网络分析还是游戏路径搜索,广度优先算法都为我们提供了一种高效而实用的解决方案。