练习:
编写函数不允许创建临时变量,求字符串的长度。
我们看到这道题,第一个想到的是不是strlen
int main()
{
char[] = "bit";
//['b']['i']['t']['\0']
//里面一共4个字符(包括结尾的、0)但是我们的strlen函数并不会计算\0的长度,所以结果应该为10
printf("%d\n",strlen(arr));
return 0;
}
那我们写求字符串长度的函数,那不就是模拟实现strlen函数吗
我们把函数命名为my_strlen
我们再来思考一下,strlen传参穿的是什么呢?
是字符串首元素的地址
返回参数应该为字符串的长度,也就是整型变量
//多以我们的函数输入参数应该这么写
int my_strlen(char* str)
{
}
里面怎么实现呢?
['b']['i']['t']['\0']//数组内容
//我们传递的参数一定是['b'],的地址,那strlen怎么知道字符串长度呢
//没错,就是去寻找['\0']
首先来看,计数怎么实现呢?
int my_strlen(char* str)
{
int count = 0;
while(*str != '\0')
{
count++;
str++;//指针的偏移
}
return count;
}
我们看一下运行结果
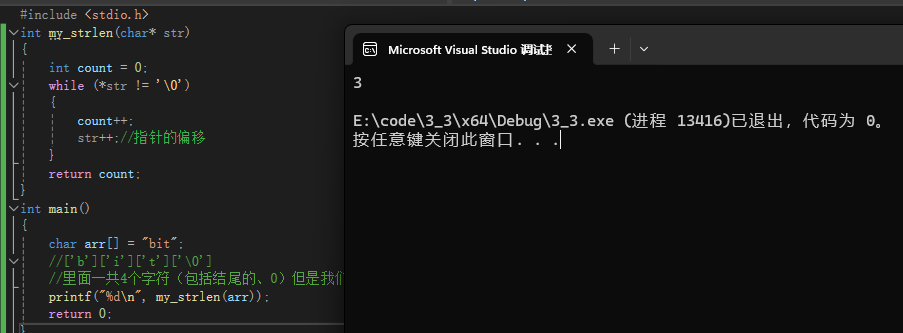
成功打印出了字符串的长度
很简单的实现方式,但是题目上要求是什么,不允许创建临时变量
我们在程序运行的过程中,创建了count作为临时变量,很明显是不对的
那我们该怎么做呢?
我们应该思考递归的想法
int my_strlen(char* str)
{
}
我们重新来,怎么才能使用递归的思想呢?
什么是递归?
程序调用自身的编程技巧称为递归( recursion)。
递归做为一种算法在程序设计语言中广泛应用。
一个过程或函数在其定义或说明中有直接或间接 调用自身的 一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解, 递归策略 只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
递归的主要思考方式在于:把大事化小
好,我们又复习了一下
大家请思考一下,我们是不是很容易就把第一个字符取出来(只判断第一个字符是不是\0)
my_strlen(“bit”);
1+my_strlen(“it”);
1+1+my_strlen(“t”);
1+1+1my_strlen(“”);
1+1+1+0
把大事化小
我们来看代码
int my_strlen(char* str)
{
if (*str != '\0')//判断第一个字符是不是结束
{
return 1 + my_strlen(str+1);//如果第一个字符不是\0的话就即为1+剩下字符的长度
}
else
return 0;
}
我们看看结果
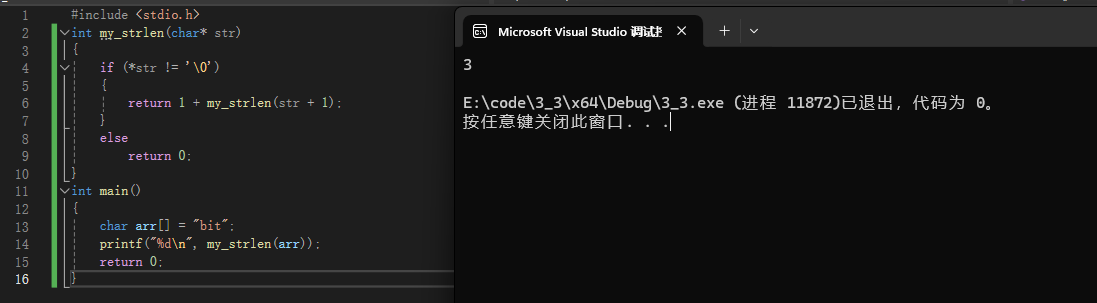
哈哈,是不是真的很神奇
还有一个问题
return 1 + my_strlen(str+1);
写为
return 1 + my_strlen(str++);
行不行?
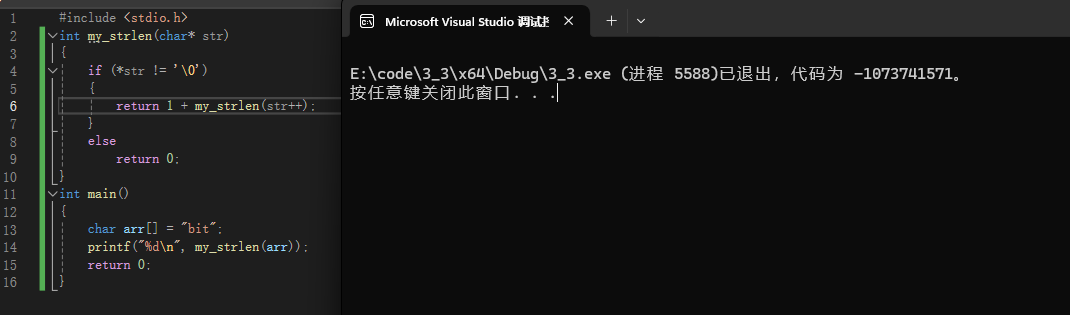
为什么不行,因为str++是后置++
后置++是干什么的,先使用再++,也就是说传进去还是原来的值,留下来的是加1后的值,是不是就和我们想要的不一样了?
改为前置++就可以了
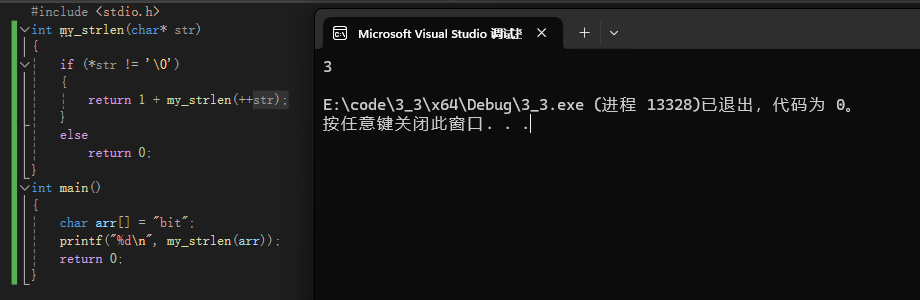
第二个练习:
求n的阶乘。(不考虑溢出)
我们还是先写主函数
int main()
{
int n;
scanf("%d", &n);
printf("%d\n", factorial(n));
return 0;
}
那递归函数该怎么写呢?
//我们可以这么想
//每一次相乘都乘自己减去一,直到为0的时候,返回1
那函数是不是能这么写
int factorial(int n)
{
if (n != 0)
return n * factorial(n - 1);
else
return 1;
}
很简单,我们来看一下结果
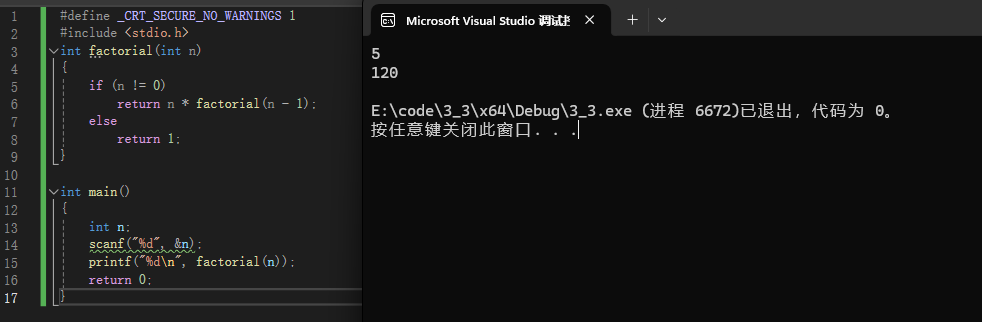
练习三:斐波那契数列
什么是斐波那契数列?
第一个数字为1,后面的数字都是前两个数字的和
那用递归的思想该怎么解决呢?
每一次迭代,都是自己加上前一个数字
return 自己上一个数字 + 上一个数字的上一个数字
当然,递归终结条件就是到2以下的时候,当自己小于等于2,直接返回1就行
是不是还是很不好理解,那我再举一个更详细的例子
我现在要求第五个斐波那契数列的数字
1.我们需要求第四个数字加第三个数字
2.我们需要求出 第二个数字+第三个数字(第四个数字) + 第一个数字+第二个数字(第三个数字)
//注意了,这里出现了循环终结条件,斐波那契数列的第一个和第二个数字都为1,那么可以直接带入
3.我们需要求出 1 + 第一个数字+第二个数字(第三个数字) + 1 +1
4.那么递归都来到了递归终结条件,开始整个程序出栈计算结果,结果就是 1+1+1+1+1 = 5
所以我们可以推导出来这个函数
int Fib(int n)
{
if(n <= 2)
return 1;
else
return Fib(n-1)+Fib(n-2);
}
看一下计算结果
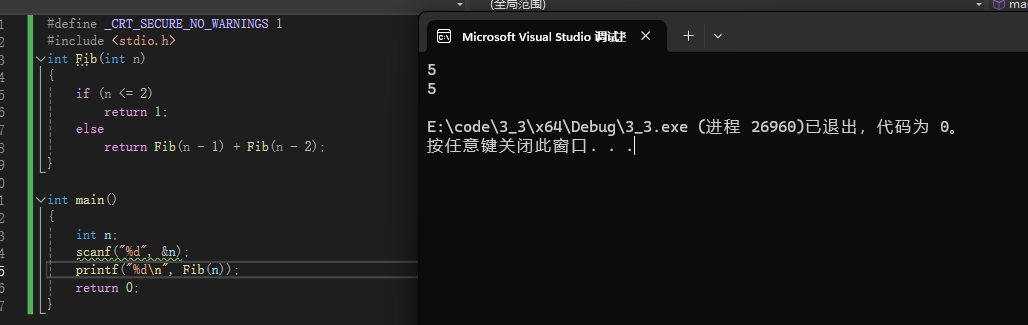
这里还有一个问题,如果我要求第五十个数字呢?
运行时你就会发现,程序一直在计算,是程序偷懒了算不出来结果吗
我们如果看一下计算过程就会发现,整个程序的复杂度是2的n次方,也就是说我如果要计算第五十个数字,需要计算1125899906842624次
效率太低 —— 重复大量的计算
那该如何避免重复的计算呢,很简单其实,我们从前往后算就行,让前两个数相加等于第三个数,一直到第n个数为止
#include <stdio.h>
int Fib(int n)
{
int i = 0;
int a = 1;
int b = 1;
int c = 1;//当不进入数列时直接返回C,所以把C初始化为1
while(n > 2)
{
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
int main()
{
int n;
scanf("%d", &n);
printf("%d\n", Fib(n));
return 0;
}
很容易理解,我们可以测试一下
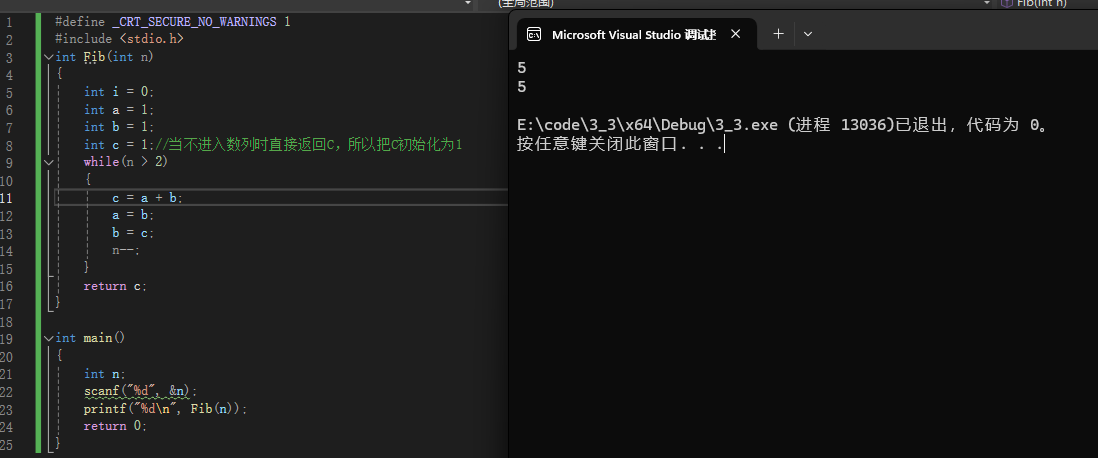
这次的时间复杂度O(n)就很低
直接计算第五十个数也是会在1秒内算出答案,但是因为整型表示范围有限溢出了,这里就不放图了
我们的代码可以用递归写,也可以用非递归来写
有时候当我们使用递归时,可能会导致栈溢出,大量的重复计算导致的效率低下
我们总是要想出一个方法要用非递归的方法来写
这个时候再难也要去找i到这样一种非递归的方法
最后一个递归问题,也是最经典的一个迭代问题
汉诺塔
经典的递归的问题

我总结一下
- 一共有三根柱子,第一根柱子有从大到小的圆盘
- 我们需要把圆盘移到第三根柱子上
- 每次只能挪动一个
- 小圆盘只能在大圆盘的上面
现在有n个圆盘那我们该如何通过程序算出来最少需要多少次移动才能成功呢?
大家可以思考一下
会尽快快更新笔记讲解这个问题的?




![蓝桥杯[OJ 1621]挑选子串-CPP-双指针](https://img-blog.csdnimg.cn/direct/00c28d4bf0a045b9a67958f18ce37e78.png)