文章目录
- Map和Set
- 一、搜索树
- 1.二叉搜索树的查找(search)
- 2.二叉搜索树的插入
- 3.二叉搜索树的删除
- 4.性能分析
- 二、搜索方法
- 1.概念
- 三、Map的使用
- 1.概念:
- 2.Map的常用方法:
- 1.V put(K Key ,V Value )
- 2.V get(Object key)
- 3.V getOrDefault(Object key, V defaultValue)
- 4.V remove(Object key)
- 5.Set<K> keySet()
- 6.Collection<V> values()
- 7.Set<Map.Entry<K, V>> entrySet()
- 8.boolean containsKey(Object key)
- 9.boolean containsValue(Object value)
- 3.Map的注意事项
- 四、Set的使用
- 1.Set的常用方法:
- 1.boolean add(E e)
- 2.void clear()
- 3.boolean contains(Object o)
- 4.boolean remove(Object o)
- 5.int size()
- 6.boolean isEmpty()
- 7.Object[] toArray()
- 8.boolean containsAll(Collection<?> c)
- 9.boolean addAll(Collection<? extends E> c)
- 10.Iterator<E> iterator()
- 2.Set的注意事项:
- 五、哈希表
- 1.概念
- 2.哈希函数
- 1.设计哈希函数:
- 2.常见的哈希函数
- 1.直接定址法(常用):
- 2.除留余数法(常用)
- 3.负载因子
- 4.解决冲突
- 1.闭散列法(开放地址法)
- 1.线性探测法:冲突的时候,放到下一个空的位置
- 2.二次探测:
- 2.开散列法(哈希桶)
- 5.HashBunk(哈希桶的实现)
- 6.HashCode方法
- HashBunk(K,V)实现
- 3.TreeMap 和 HashMap 的区别:
- 4.TreeSet 和 HashSet 的区别:
Map和Set
-
HashMap和HashSet的底层是一个哈希表
-
TreeMap 和TreeSet的底层是一棵搜索树(红黑树)
-
涉及到一些搜索查找的场景可以调用Map和Set接口
一、搜索树
二叉搜素树 ( 二叉排序树 )
1.要么是空树
2.如果左子树不为空,则左子树上所有节点的值都小于根节点的值
3.如果右子树不为空,则右子树上所有节点的值都大于根节点的值
4.它的左右子树也是二叉搜索树
5.对二叉搜索树进行中序遍历,就能得到一个有序的数组
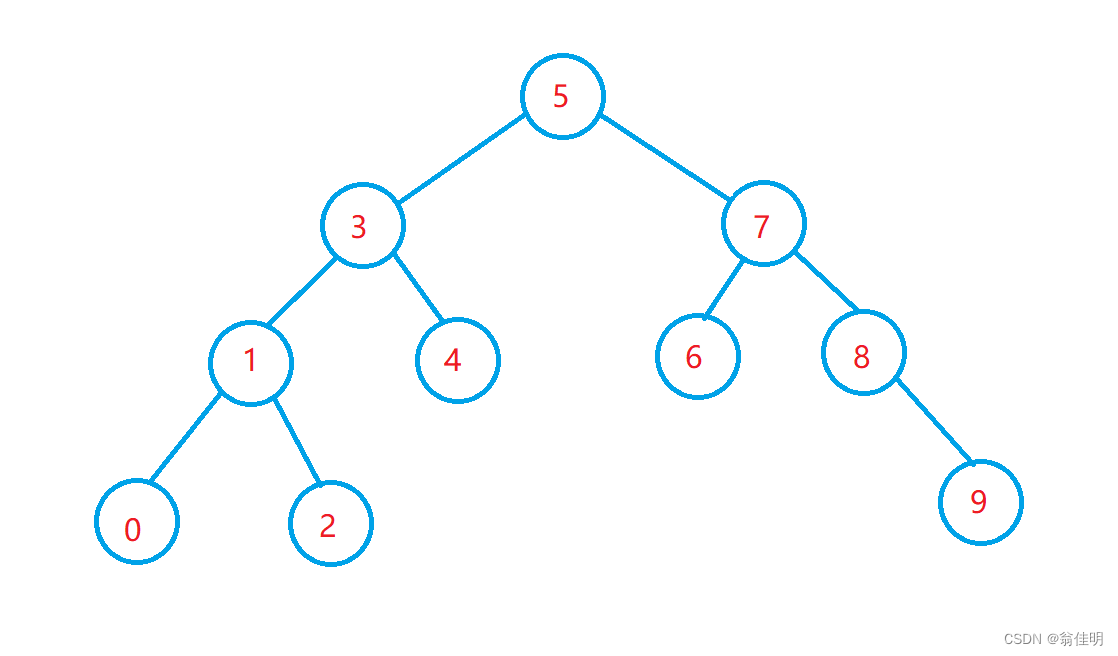
1.二叉搜索树的查找(search)
-
将要查找的值,和根节点比较
-
比根节点小的在左树找,比根节点大的在右树找
最坏情况:按单分支树找,时间复杂度为树的高度 N
最好情况:完全二叉树、满二叉树,时间复杂度为树的高度:log2N,效率最高
为了解决单分支树的问题,采用AVL树解决。
- AVL树:高度平衡的二叉搜索树,保证高度一直平衡(左右高度差不超过1),需要不断进行旋转(左旋、右旋、先左在右、先右再左),来保持平衡
- 红黑树:加入了颜色,减少了旋转
public class BinarySearchTree {
static class TreeNode {//静态内部类
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public TreeNode root = null;
/**
* 查找二叉搜索树中指定的val值
*
* @param val
* @return
*/
public TreeNode find(int val) {
TreeNode cur = root;
while (cur != null) {
if (cur.val == val) {
return cur;
} else if (cur.val < val) {
cur = cur.left;
} else {
cur = cur.right;
}
}
return null;
}
- 1.设cur结点为root位置
- 2.cur的val如果小于目标val,cur移动到左子树
- 3.cur 的val如果大于目标val,cur移动到右子树
2.二叉搜索树的插入

- 1.如果是空树(root==null),直接插入根的位置
- 2.如果不是空树,按照查找的逻辑找到要插入的位置,插入新结点
- 3.都插入到了叶子结点,也就是cur为空时的位置
- 4.所以要记录一个cur的双亲结点,来和val比较,决定cur==null时,插入的方向
/**
* 插入一个数据
*
* @param val
*/
public void insert(int val) {
//root为空
if (root == null) {
root = new TreeNode(val);
return;
}
//root不为空
TreeNode cur = root;
TreeNode parent = null;
//找到cur为空的位置
while (cur != null) {
if (cur.val < val) {
parent = cur;
cur = cur.right;
} else if (cur.val > val) {
parent = cur;
cur = cur.left;
} else {
return;
}
}
//根据判断双亲结点的值来决定插入那个叶子结点
TreeNode node = new TreeNode(val);
if (val < parent.val) {
parent.left = node;
} else {
parent.right = node;
}
}
public void inorder(TreeNode root) {
if (root == null) {
return;
}
inorder(root.left);
System.out.print(root.val + " ");
inorder(root.right);
}
3.二叉搜索树的删除
要删除的位置为cur,它的双亲结点为parent
-
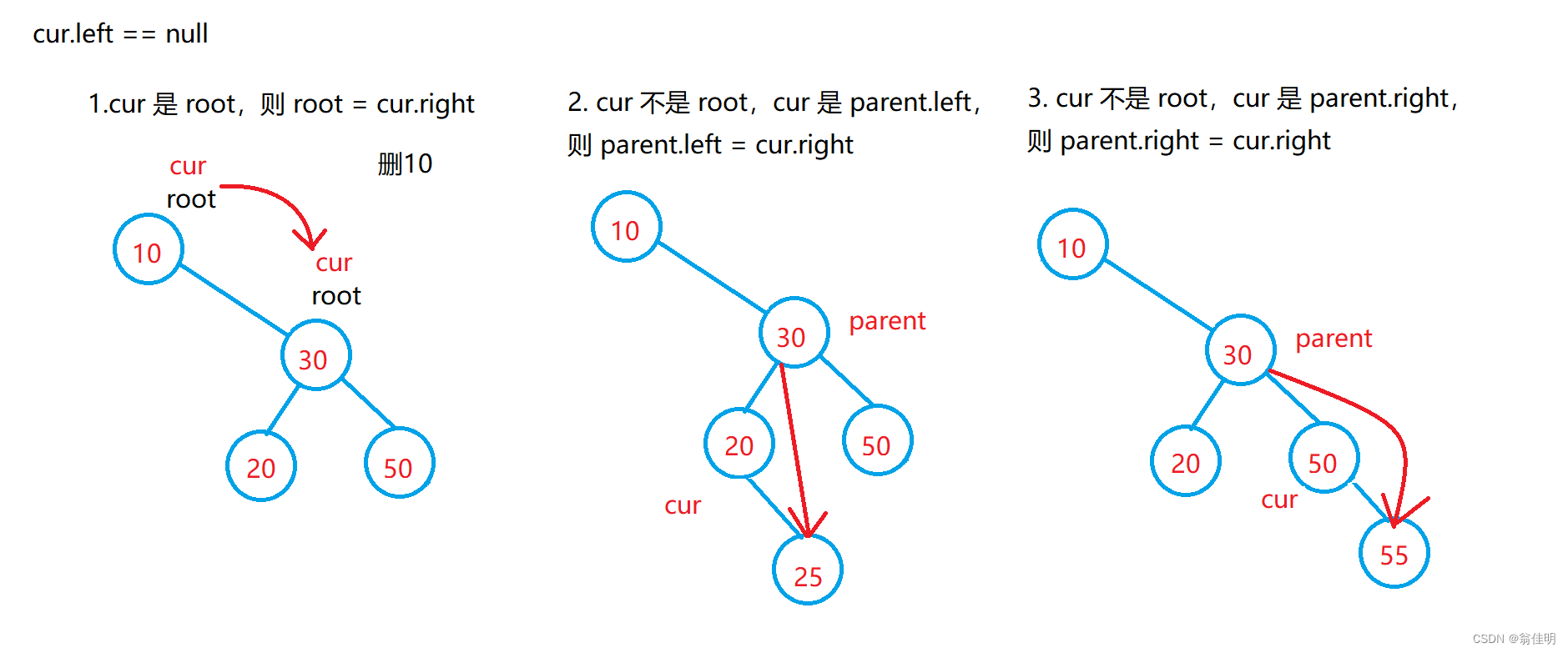
1.cur左结点为空:cur.left == null
1.cur为根节点,cur没有左树,根节点移动到它的右树上
2.cur不是根节点,此时cur为双亲结点的左结点,cur没有左树,双亲结点的左结点连上cur的右结点 parent.left = cur.right
3.cur不是根节点,此时cur为双亲结点的右结点,cur没有左树,双亲结点的右结点连上cur的右结点 parent.right = cur.right
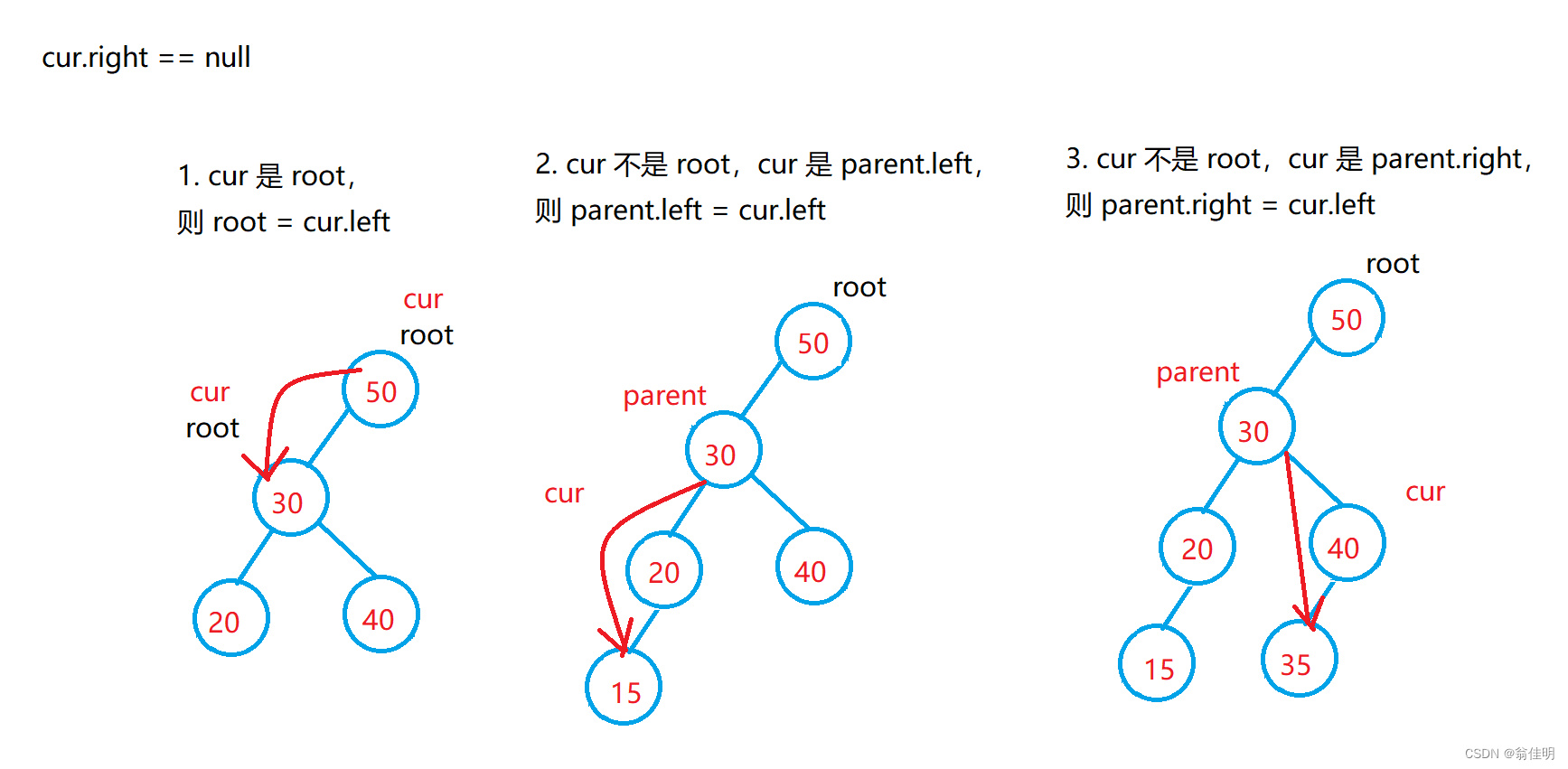
- 2.cur右结点为空:cur.right == null
1.cur为根节点,cur没有右子树,根节点移动到cur的左子树上
2.cur不是根节点,cur是双亲结点的左结点,cur没有右结点,双亲结点的左结点连上cur的左结点
3.cur不是根节点,cur是双亲结点的右结点,cur没有右结点,双亲结点的右结点连上cur的左结点
3.左右结点都不为空:cur.left != null && cur.right != null
1.替换法进行删除,在cur的右子树中,找到该子树的最小值,和要删除的值交换
2.最后删除那个替换的结点,维护了二叉搜索树
3.替换的结点在它双亲结点的左边,没有左子树,target.left== nulll,如果有右子树,target双亲结点的左结点连接target的右结点(target的右结点都比target大),没有右子树,连接的是空值
4.替换的结点在它双亲结点的右边(双亲结点没有左结点),target双 亲结点的右结点连接target的右结点

/**
* 删除值为val的结点
*
* @param val
* @return
*/
public void remove(int val) {
TreeNode cur = root;
TreeNode parent = null;
//找到cur结点的位置
while (cur != null) {
if (cur.val == val) {
removeNode(cur, parent);
return;
} else if (val < cur.val) {
parent = cur;
cur = cur.left;
} else {
parent = cur;
cur = cur.right;
}
}
}
/**
* 删除结点的分类情况
*
* @param cur
* @param parent
*/
private void removeNode(TreeNode cur, TreeNode parent) {
if (cur.left == null) {
//cur的左结点为空
if (cur == root) {
root = cur.right;
} else if (cur == parent.left) {
parent.left = cur.right;
} else {
parent.right = cur.right;
}
} else if (cur.right == null) {
//cur的右结点为空
if (cur == root) {
root = cur.left;
} else if (cur == parent.left) {
parent.left = cur.left;
} else {
parent.right = cur.left;
}
} else {
//cur的左右结点都不为空
TreeNode target = cur.right;//在右树中找最小值
TreeNode targetParent = cur;
while (target.left != null) {
targetParent = target;
target = target.left;
}//找最小值
cur.val = target.val;//替换
if (target == targetParent.left) {
targetParent.left = target.right;
//目标值在双亲结点的左边
} else {
targetParent.right = target.right;
//目标值在双亲结点的右边
}
}
}
4.性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能
- 即结点越深,则比较次数越多
- 插入的次序不同,可能得到不同结构的二叉搜索树
最好情况:二叉搜索树为完全二叉树,平均计较次数:log2N
最坏情况:二叉树退化成单分支树,平均比较次数为 N/2
- 因为TreeSet和TreeMap的底层是红黑树,所以每次存储元素时,都得进行大小比较。
- 所以存放到这两个集合类的数据,一定是可以比较的
二、搜索方法
1.概念
-
1.Map和Set是一种专门用来进行搜索的容器/数据结构,搜索的效率和具体实例化的子类有关。
分别实例化TreeMap、HashMap,两者存在效率上的差别。
Map<String,Integer>map1 =new TreeMap<>();//查找的复杂度为o(logN) Map<String,Integer>map2 =new HashMap<>();//查找的复杂度为o(1) // TreeMap的底层是搜索树 // HashMap的底层是哈希表:数组+链表+红黑树组成 -
2.常见的搜索方法为 静态查找,一般不进行插入、删除。
1,直接遍历: 时间复杂度为 o(N),元素越多,效率越慢。
2.二分查找:时间复杂度为 o(log2N),要求搜索前必须是有序的。
-
3.而Map和Set是可以进行 动态查找 的集合容器。
-
4.只有关键字的叫纯Key模型(Set),由关键字和其对应的值形成的键值对,叫Key-Value模型(Map)
三、Map的使用
1.概念:

- Map是一个接口类,没有继承于Collection。
- 存储的形式是 Key-Value 键值对,并且Key是唯一的,不能重复。
2.Map的常用方法:
1.V put(K Key ,V Value )
设置Key对应的Value,将元素对应的值进行存储
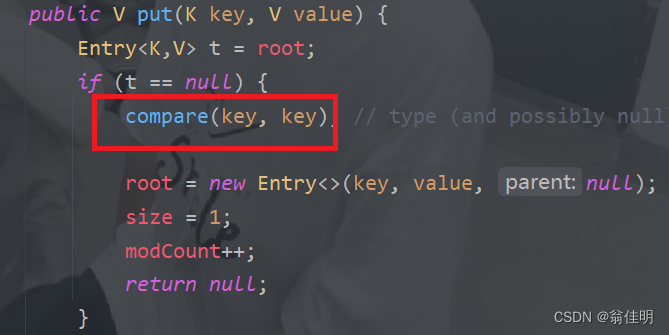
- Map的底层是一棵搜索树,在放进搜索树的时候要进行比较,比较的对象是关键字Key
public static void main(String[] args) {
Map<String,Integer>map1 =new TreeMap<>();//查找的复杂度为o(logN)
map1.put("Math",3);
map1.put("Chinese",2);
map1.put("English",4);
System.out.println(map1);
}
//{Chinese=2, English=4, Math=3}
2.V get(Object key)
- 返回对应的value,通过Key得到对应的值
System.out.println(map1.get("Math"));//2
System.out.println(map1.get("Art"));//null
如果get传进的Key不存在,则返回的Value值为null
3.V getOrDefault(Object key, V defaultValue)
-
返回 key 对应的 value,key 不存在,返回默认值
map1.put("Math",3); System.out.println(map1.getOrDefault("Science", 7));//7 System.out.println(map1.getOrDefault("Math", 7)); //3如果给的Key值在Map中存在,返回原本的Value,忽视自己填的默认值
4.V remove(Object key)
- 根据Key来删除K-V的映射关系
System.out.println(map1.remove("English"));//4
System.out.println("++++++");
System.out.println(map1.containsValue(4)); //false
System.out.println(map1.containsKey("English"));//false
再remove()中传入Key, key和其对应的Value均删除
remove()返回删除的Value
5.Set keySet()
- 返回所有 key 的不重复集合 ,返回的是一个set
Set<String>set = map1.keySet();
System.out.println(set);//[Chinese, English, Math]
6.Collection values()
- 返回所有 value 的可重复集合
Collection<Integer> values = map1.values();
System.out.println(values);//[2, 4, 3]
7.Set<Map.Entry<K, V>> entrySet()
-
返回所有的 key-value 映射关系
-
将map的Key和Value看作一个整体(Entry),Set中存放不同的Entry
Set<Map.Entry<String, Integer>> entrySet = map1.entrySet();
for (Map.Entry<String, Integer> entry : entrySet) {
System.out.println("Key:"+entry.getKey()+" Value:"+entry.getValue());
}
//Key:Chinese Value:2
//Key:English Value:4
//Key:Math Value:3
8.boolean containsKey(Object key)
- 判断是否包含 key
System.out.println(map1.containsKey("Chinese"));//true
9.boolean containsValue(Object value)
- 判断是否包含Value
System.out.println(map1.containsValue(3));true
3.Map的注意事项
- 1.Map是一个接口,不能直接实例化对象。只能实例化它的实现类TreeMap和HashMap
- 2.Map中存放键值对中的Key是唯一的,Value不唯一
map1.put("English", 4); map1.put("English",44);如果存储相同的Key,会覆盖掉之前的Value.
-
3.在TreeMap中插入键值对时,Key不能为空,否则会抛出空指针异常,
Value可以为空。HashMap的Key和Value都可以为空
-
4.Map中的Key因为不能重复,可以全部用keySet分离出来,存进Set中。Value也可以分离出来,存在Collection的任何一个子集合中(可以重复)
-
5.Map中的键值对,Key不能直接修改,Value可以直接修改。如皋要修改Key,需要先删除Key,再重新插入
四、Set的使用
- 和Map不同的是,Set继承于Collection。Set中只存储了Key
1.Set的常用方法:
1.boolean add(E e)
- 添加元素,如果存在则无法添加。
Set<String>set = new TreeSet<>();
set.add("Hello");
set.add("World");
boolean happy = set.add("Happy");
boolean hello = set.add("Hello");
System.out.println(set);//[Happy, Hello, World]
System.out.println(happy);//true
System.out.println(hello);//false
2.void clear()
set.clear();
- 清空集合
3.boolean contains(Object o)
System.out.println(set.contains("Hello"));//true
System.out.println(set.contains("hello"));//false
- 判断元素在集合中是否存在
4.boolean remove(Object o)
System.out.println(set.remove("Hello"));//true
System.out.println(set.remove("hello"));//false
- 删除集合中的元素,返回值为布尔类型
5.int size()
System.out.println(set.size());//2
- 返回集合的大小
6.boolean isEmpty()
System.out.println(set.isEmpty());//false
- 判断集合是否为空
7.Object[] toArray()
System.out.println(set);//[Happy, World]
System.out.println(set.toArray());//[Ljava.lang.Object;@4554617c
- 将Set中的元素转化为数组返回
8.boolean containsAll(Collection<?> c)
Deque<String> deque = new ArrayDeque<>();
deque.add("Happy");
deque.add("World");
System.out.println(set.containsAll(deque));//true
-
判断集合c中的元素是否在set中全部存在,是返回true,否则返回 false
只要继承了Collection的类都可以比较
9.boolean addAll(Collection<? extends E> c)
Deque<String> deque = new ArrayDeque<>();
deque.add("Happy");
deque.add("World");
deque.add("adddadd");
System.out.println(set.containsAll(deque));//true
System.out.println(set.addAll(deque));//true
System.out.println(set);//[Happy, World, adddadd]
- 将集合c中的元素添加到set中,可以达到去重的效果
10.Iterator iterator()
- 返回迭代器
- 继承自iterable的类都可以使用,HashMap和TreeMap不支持使用迭代器遍历,只能把map转化成Set
Iterator<String> iterator = set.iterator();
while (iterator.hasNext()){
System.out.println(iterator.next());
}//Happy
//World
如果有下一个,打印下一个
2.Set的注意事项:
1.Set是继承自Collection的一个借口类
2.Set中只存有Key,且Key唯一.Key不能修改,修改要先删除,再重新插入
3.TreeSet的底层是用Map实现的
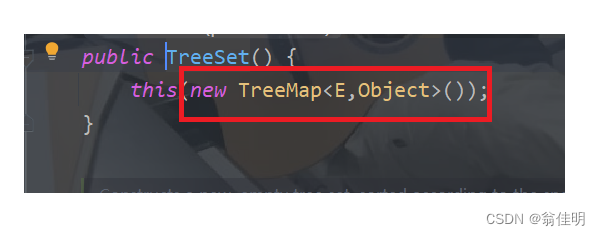
new 的TreeSet,实际上new的是一个TreeMap对象。这个TreeMap的Value都是一个Object对象
TreeSet不能插入为null的Key,HashSet可以,因为TreeSet是需要比较的
4.Set的最大功能是对集合进行去重。
Key不能重复且唯一
5.Set的常用接口的TreeSet和HashSet,
LinkedHashSet在HashSet的基础上,维护了双向链表,来记录元素的插入顺序
五、哈希表
1.概念
- 查找的时间复杂度:二分查找为 o(N),搜索树为o(log2N) 哈希表为 o(1)
- 通过关键字Key来快速找到对应的值,不比较,直接找到。
- 通过一个函数将关键字和存储位置直接建立一一对应的关系,从而避免了不断的比较查找
这种映射的方法叫哈希(散列)方法,函数叫哈希函数,构造的结构叫哈希表(HashTable)
2.哈希函数
hash(key) = key % capacity
capacity是存储空间的大小
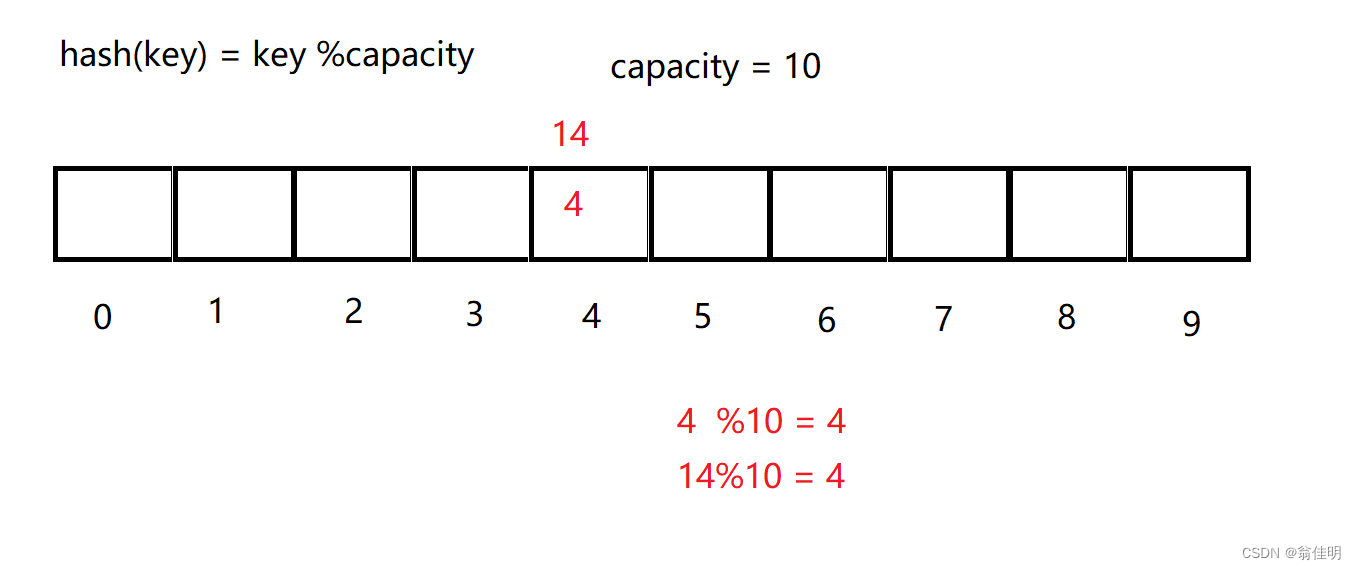
- 哈希冲突:当两个不同的值,经过哈希函数,得到相同的地址时,发生哈希碰撞
- 发生冲突的原因:1.存储的容量小于要存储的数量。2.哈希函数的设计不合理
- 哈希冲突无法解决,只能尽量降低冲突率
1.设计哈希函数:
1.要足够简单
2.计算的地址在空间中均匀分布
3.有m个地址,值域为0到m-1
2.常见的哈希函数
1.直接定址法(常用):
Hash(Key)= A*Key + B 关键字的线性函数
- 优点:简单、均匀
- 缺点:需要事先知道关键字的分布情况
- 场景:查找比较小且连续的数
2.除留余数法(常用)
Hash(key) = key% p(p<=m)
3.负载因子
负载因子 a = 填进表中的元素个数 / 哈希表的长度
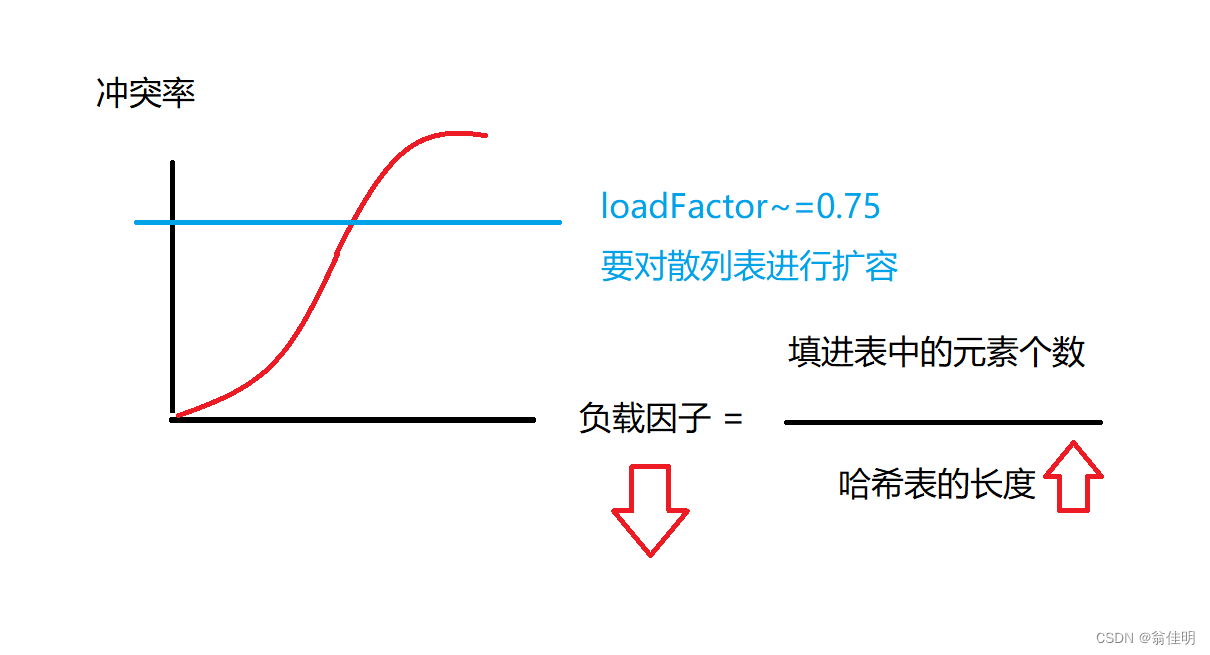
4.解决冲突
1.闭散列法(开放地址法)
1.线性探测法:冲突的时候,放到下一个空的位置
- 缺点:将冲突的元素放在了一起

2.二次探测:
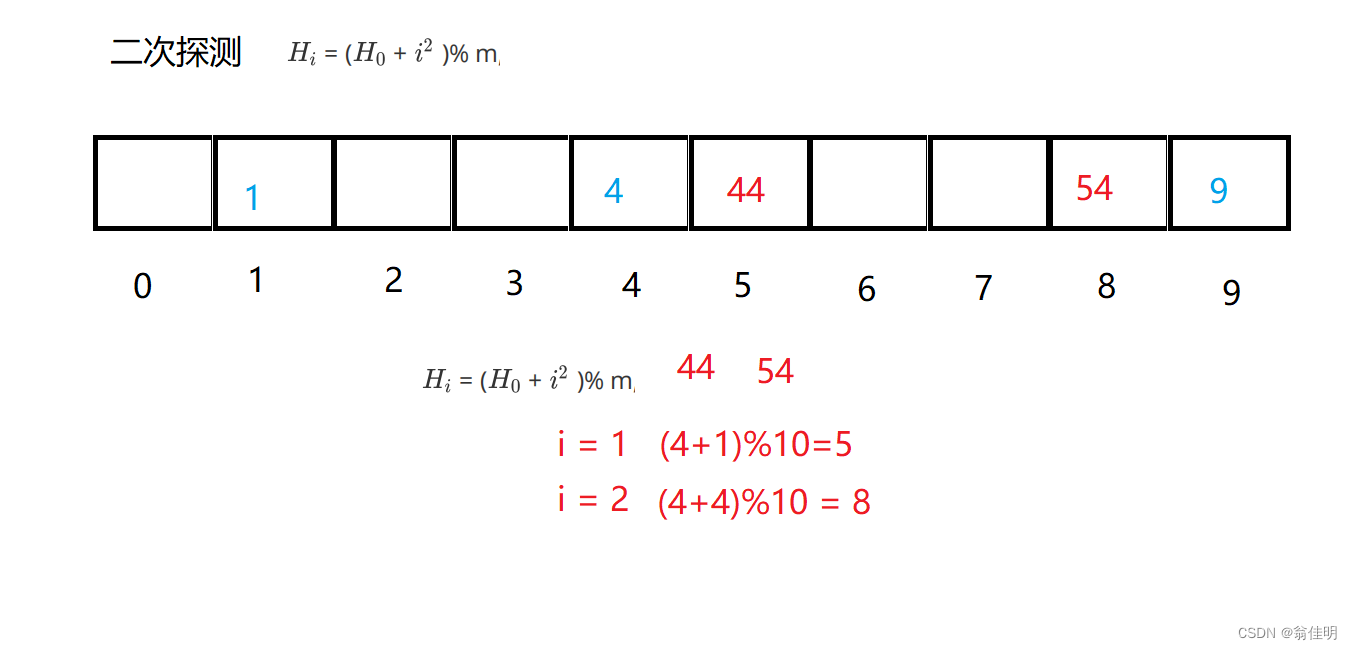
- 缺点:空间利用率低
- 解决了线性探测聚到一起的问题
- 超过0.5要扩容
2.开散列法(哈希桶)
- 也叫链地址法、开链法
- 数组+链表 :数组的每个元素就是链表的头结点
- 数组+链表+红黑树(当数组长度>=64 && 链表长度 >=8 以后,把链表变成红黑树,小于又变回去【树化、解树化】)

JDK7以前:用头插法存进数组中的链表
JDK8以后:采用尾插法
5.HashBunk(哈希桶的实现)
哈希桶的结构
public class HashBunk {
static class Node {
int key;
int val;
Node next;
public Node(int key, int val) {
this.key = key;
this.val = val;
}
}
public Node[] array;
public int usedSize;
public static final float DEFAULT_LOAD_FACTOR = 0.75f;//负载因子
public HashBunk() {
array = new Node[10];
}
}
哈希桶的插入:采用尾插法实现
/**
* 哈希桶的插入
*
* @param key
* @param val
*/
public void put(int key, int val) {
int index = key % array.length;
//找到要插入的链表所在数组的下标标
Node cur = array[index];
//遍历index处的链表,看是否存在Key,
// 存在,跟新val
//不存在,进行尾插法
while (cur != null) {
if (cur.key == key) {
cur.val = val;//key存在,更新val
return;
}
cur = cur.next;
}
if (array[index]==null){
Node node = new Node(key, val);
array[index]=node;
usedSize++;
}else {
cur = array[index];
while (cur.next!=null){
cur = cur.next;
}
//进行尾插法
Node node = new Node(key, val);
cur.next = node;
node.next = null;
usedSize++;
}
//计算当前负载因子
if (doLoadFactor() > DEFAULT_LOAD_FACTOR) {
//进行扩容,不光要改变数组的大小,还要重新确定链表的首地址
//因为之前的首地址是按照之前的容量大小计算出来的。
resize();
}
}
数组大小的扩容,同时要重新确定链表中每个结点的位置
private void resize() {
Node[] newArray = new Node[2 * array.length];
for (int i = 0; i < array.length; i++) {
//遍历原来的数组
Node cur = array[i];
//得到原来数组的首结点
while (cur != null) {
//遍历链表
int newIndex = cur.key % newArray.length;
Node tmp = cur.next;
Node node = cur;
node.next = null;
if (newArray[newIndex] == null) {
newArray[newIndex] = node;
} else {
Node lastNode = getLastNode(newArray[newIndex]);
lastNode.next = node;
}
cur = tmp;
}
}
array = newArray;
}
private Node getLastNode(Node cur) {
while (cur.next != null) {
cur = cur.next;
}
return cur;
}
private float doLoadFactor() {
return usedSize * 1.0f / array.length;
}
public int get(int key){
int index = key%array.length;
Node cur = array[index];
while (cur!=null){
if (cur.key==key){
return cur.val;
}
cur = cur.next;
}
return -1;
}
6.HashCode方法
- 当传入对象,转化成整数进行比较
- HashCode在Object的类中(是一个native方法,看不到)
- 所以要对HashCode进行重写
HashMap<Student,Integer>map = new HashMap<>();
Student student1 = new Student("小王",001);
Student student2 = new Student("小王",001);
System.out.println(student1.hashCode());//1163157884
System.out.println(student2.hashCode());//1956725890
- 当没有重写HashCode方法,而是采用默认的,此时,HashCode的值不同
@Override
public boolean equals(Object o) {
if (this == o) return true;
if (o == null || getClass() != o.getClass()) return false;
Student student = (Student) o;
return id == student.id && Objects.equals(name, student.name);
}
@Override
public int hashCode() {
return Objects.hash(name, id);
}
- 当重写了HashCode方法(equals顺便一起生成),此时,HashCode的值一样
System.out.println(student1.hashCode());//1163157884
System.out.println(student2.hashCode());//1956725890
map.put(student1,2);
System.out.println(map.get(student2));//2
//23565798
//23565798
- 由于两个对象的id和name相同,同时重写了HashCode方法。因此两个的HashCode值相同,所以get student2 得到的val就是student1的val。
HashBunk(K,V)实现
public class HashBunk2<K, V> {
static class Node<K, V> {
public K key;
public V val;
public Node<K, V> next;
public Node(K key, V val) {
this.key = key;
this.val = val;
}
}
public Node<K, V>[] array;
public int usedSize;
public static final float DEFAULT_LOAD_FACTOR = 0.75f;
public HashBunk2() {
array = (Node<K, V>[]) new Node[10];
}
public void put(K key, V val) {
int hash = key.hashCode();
int index = hash % array.length;
Node<K, V> cur = array[index];
while (cur != null) {
if (cur.key .equals(key)) {
cur.val = val;
//更新Val
return;
}
cur = cur.next;
}
Node<K, V> node = new Node<>(key, val);
node.next = array[index];
array[index] = node;
usedSize++;
}
public V getValue(K key) {
int hash = key.hashCode();
int index = hash % array.length;
Node<K, V> cur = array[index];
while (cur != null) {
if (cur.key.equals(key) ) {
return cur.val;
}
cur = cur.next;
}
return null;
}
-
HashCode方法是为了在数组中找到对应的位置
-
equals方法是用来判断该位置链表中的元素是否有目标元素
-
类似于查字典,先找到哪一页,再找到具体的字
-
以后在写自定义对象时,要先验证一下equals和HashCode
3.TreeMap 和 HashMap 的区别:
| Map | TreeMap | HashMap |
|---|---|---|
| 底层结构 | 红黑树 | 哈希桶 |
| 插、删、查找的时间复杂度 | o(log2N) | o(1) |
| 是否有序 | Key有序 | 无序 |
| 线程安全 | 不安全 | 不安全 |
| 插、删、查找区别 | 进行元素比较 | 哈希函数计数哈希地址 |
| 比较与覆写 | Key必须可以比较 | 自定义类型要重写equals和HashCode |
| 应用场景 | 需要Key有序 | 需要更高的时间性能 |
4.TreeSet 和 HashSet 的区别:
| Set | TreeSet | HashSet |
|---|---|---|
| 底层结构 | 红黑树 | 哈希桶 |
| 插、删、查找的时间复杂度 | o(log2N) | o(1) |
| 是否有序 | Key有序 | 不一定有序 |
| 线程安全 | 不安全 | 不安全 |
| 插、删、查找区别 | 按红黑树的特性 | 计算哈希地址 |
| 比较与覆写 | Key必须可以比较 | 自定义类型要重写equals和HashCode |
| 应用场景 | 需要Key有序 | 需要更高的时间性能 |
点击移步博客主页,欢迎光临~