知识蒸馏Matching logits
公式推导
刚开始的怎么来,可以转看下面证明梯度等于输出值-标签y

C是一个交叉熵,我们要求解的是这个交叉熵对的这个梯度。
就是你可以理解成第
个类别的得分。
就是student model,被蒸馏的模型,它所输出的logits。
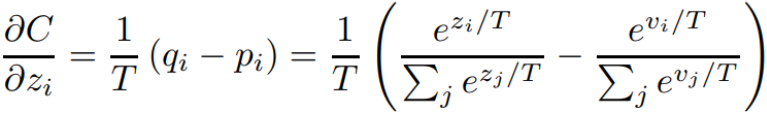
是什么?是target probability对吧。
是什么?
认为就是这个distilled model的输出的那个probability。所以就是说这两个概率相减,再乘以这个T分之一T是什么?T是一个温度。
我们现在假定是说我们是用teacher model输出的这个label,然后去训练student model,或者说去训练distilled model。我们对这个第个类别的梯度,就等于
,然后呢,
和
可以做一个化简。
对和
进行展开,概率都是用softmax算出来的,就可以得到这个式子。
通过来进行化简,这个式子在
比较小的时候是成立的。
在这里,当足够大的时(相比
的logits,即
),
就足够的小,接近于0,此时

的这个累加,它就等于零。这个
的这个累加也等于零,即
,所以这两个分母直接就变成了N。
则所求梯度
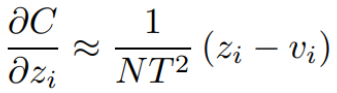
想说明的事情
它其实就想说明这样一个事情。我们试图用一个teacher model,或者说我们想用VI对应的那个概率叫。
对应的概率叫
。如果我们想用这个
作为label去用交叉商去训练
去用这个soft label的交叉商去训练
,那么其实我们可能不需要套用交叉商这个东西了,我们也不需要什么softmax的label的交叉商,然后去做这个事了。因为这个东西在我们的这样一通推导下就会发现,其实就等于均方误差,右边这一项其实就是什么均方误差的求导,它就是均方误差求导之后的结果,你可以这样认为。
我们就会发现说,原来对于交叉商对于这个知识蒸馏的这个交叉商,然后我们对他求导求出来的梯度其实是近似等同于我们直接用MSE去训练,然后得到的梯度的。那么既然这样,我们为什么不直接用MSE?
它的推导就告诉我们说我们对于两个模型,两个多分类模型来说,我们要用a模型去交B模型做蒸馏。我们没有必要让这两个模型生成分别生成什么label,然后再生成预测的概率,然后再加上去优化了。
我们直接让这两个多分类模型的这个logic,然后直接做MSE就可以了,就可以做到一种就是一种这种MSE就是一种什么蒸馏的特殊形式。就是蒸馏的一个最早期的雏形,其实在这个时候都还没有考虑用这个什么KL散度来做,就只是提出最简单的一个思想是什么,就是用MSE来做就够了。
我们一直即便到今天,我们做很多知识正溜的实验,我们依然会发现MIC可能有的时候都会比K要好。虽然大家都说自己用什么KL散度用什么JS散度,但是就是否现在就最优,还真不一定有的时候就是MSE效果好。
注:
需要注意的事
公式的推导基于两个假设:
1.得足够大的(相比
的logits,即
)
2.模型输出的logic是零均值的(即均值为0),因为模型输出的logic是零均值的,这个的这个累加,它就等于零。这个
的这个累加也等于零,即
证明梯度等于输出值-标签y
softmax函数
归一化,使其输出的概率和为1
代表的是第
个神经元的输出。
神经元的输出,一个神经元如下图:

其中是第i个神经元的第j个权重,b是偏移值。
表示该网络的第i个输出。
给这个输出加上一个softmax函数,得
代表softmax的第i个输出值
交叉熵损失函数 loss function
其中表示真实的分类结果。
证明梯度等于输出值-标签y
loss对于神经元输出的梯度为
由于softmax公式的特性,它的分母包含了所有神经元的输出,对于不等于i的其他输出里面,也包含着,所有的a都要纳入到计算范围中,并且后面的计算可以看到需要分为
和
两种情况求导。
由于
如果:
这里
如果:
这里
综上
最后,针对分类问题,我们给定的结果最终只会有一个类别是1,其他非标签类别都是0,因此,对于分类问题,这个梯度等于
知识蒸馏RocketQAv2
https://arxiv.org/pdf/2110.07367.pdf

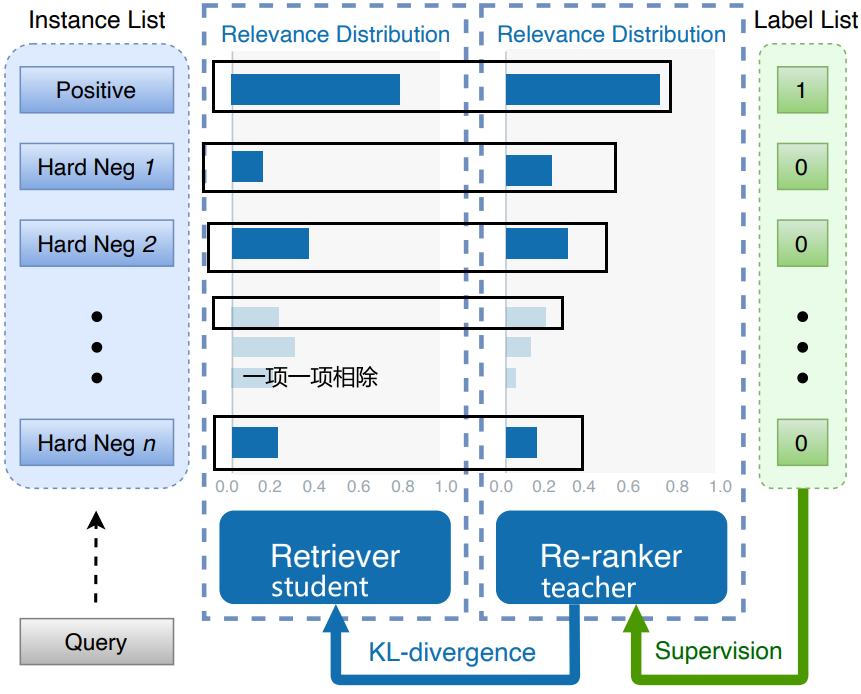
这个模型有两部分组成一个retriever和一个ranker。这个做的事情就是说用label去监督re-ranker,然后用ranker去监督retriever。用KL散度去约束它约束,用这个K散路去让这个re-ranker的分布和retriever的分布对齐。
要注意就是说。这里就是他们就没有用MSE,就是说如果用MSE怎么做,就是说对应的这个直接相减,就对应位置直接相减,然后分MSE就行。这里用的是KL散度。
KL散度的定义,你可以认为是这样的,让这两个概率分别相除,除完了之后都要再取对数,然后再乘以这个概率。

DE,这个teacher model的概率乘以teacher model的概率乘以log,teacher model的概率除以student model的概率。然后把这么多概率给它都累加起来。
在这里,假定这里的是retriever给出来的一个概率分布假如说是十个候选,ranker也给了这样一个概率分布,那么就是十个概率分布对应的一项一项的去算这个KL度,即概率除概率,然后再取对数,然后再乘上ranker这个概率。
然后再把这十项给它累加起来,然后就是一个KL散度,这样的话,这个K散度其实是现在就是接受最多的一种损失函数。
因为KL散度就是天生的,可以捕获这个分布和分布之间的距离。像MSE缺点是什么?MSE的缺点是它没有整体的那种距离衡量的能力。MSE其实是对于细节的这种距离的衡量很强。如果MSE来的话,每一个每一项,这十项每一项的重要性对于MIC来说都是一样的。但是这个KL散度可能就会更在乎一个整体的一个分布上的一个区别了,就而不是说就在乎一些细节上的一些差别,因为有可能就是说。你某一些细节差距虽然大一些,但是你整体差距不大,所以KL散度也可以比较小。
实际上一切可以衡量两个分布之间距离的指标都可以用来做知识蒸馏,所以其实wasserstein距离也可以用来作为蒸馏的损失函数:
https://openaccess.thecvf.com/content/CVPR2021/papers/Chen_Wasserstein_Contrastive_Representation_Distillation_CVPR_2021_paper.pdf
为什么知识蒸馏会有效?
1. teacher model可以生成soft label,相比于原始数据的hard label,包含了更多信息量。
所以很多时候你与其说直接用一个数据集去训练一个模型,你还不如用这个数据集先训练一个大a模型比a模型要大的模型。再让大a模型去教会a模型去做,有可能效果就更好。就是因为大a模型这个teacher model可以生成soft label相比于原始数据的hard label,可以包含更多的信息量,从而就天然的有一种去燥的一种功能。
2. teacher model可以为大量的无标签数据打上label,然后为student提供一个大规模的训练集。然后从而可以给student提供一个更大尺度的训练集,然后防止student的一个过拟合,然后提高student model的一个泛化能力。也就是说,teacher model可以把自己的泛化能力交给student model。
在这个知识蒸馏的过程当中,这也是为什么说很多大公司里边现在线上的模型都是蒸馏出来的小模型就是因为我们与其说直接训练小模型。还不如说就用这个蒸馏去蒸馏一个小模型反而泛化能力会更强一些。