目录
每日文案
一、线性表的定义
二、线性表的操作
顺序表的存储结构
顺序表的初始化操作
判断顺序表是否为空表
将顺序表置为空表
计算顺序表中的元素个数
取出顺序表中的对应位置元素
取出对应数值的位序
在对应位置插入元素
将对应位置的元素删除
将顺序表中的数据打印出来
将顺序表A和B进行合并
总结
每日文案
失去的东西,其实从来未曾真正属于的属于你,也不必惋惜
一、线性表的定义
线性表是:零个或者多个数据元素的有限序列
这里我强调几个地方,首先是序列,那么就是有序的,如果说有多个元素,那么第一个元素就没有前驱的,最后一个元素是没有后继的,其他的元素有且仅有一个前驱和后继。就像是幼儿园开小火车,如果一个小朋友去拉后面两个小朋友的衣服那么就不可以排成一队了,如果多个小朋友拉扯那就是在打架了.
然后线性表强调的是有限性,线性元素的个数n定义为线性表的长度,如果n=0那么线性表就是一个空表,并且每个数据元素都有确定的位置,比如说a1是第一个元素,那么他的位序就是1 同理Ai 就是在线性表的位序就是i
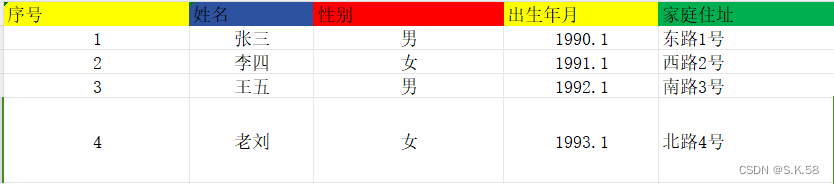
这里举个例子,班级同学的花名册,其中包含着同学的学号,姓名,性别等等信息构成一个表这个也是一个线性表,这里需要强调一个概念,在复杂的线性表中,一个数据元素可以由若干个数据项组成,这里我们表格里面的姓名学号这些都是数据项,他们连起来构成了数据元素,最后串起来构成了数据项
二、线性表的操作
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存储空间初始分配量 */
typedef int ElemType; /* ElemType类型根据实际情况而定,这里假设为int */
typedef struct
{
ElemType data[MAXSIZE]; /* 数组,存储数据元素 */
int length; /* 线性表当前长度 */
}SqList;
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */-
顺序表的初始化操作
/* 初始化顺序线性表 */
Status InitList(SqList *L)
{
L->length=0;
return OK;
}-
判断顺序表是否为空表
/* 初始条件:顺序线性表L已存在。操作结果:若L为空表,则返回TRUE,否则返回FALSE */
Status ListEmpty(SqList L)
{
if (L.length == 0)
return TRUE;
else
return FALSE;
}-
将顺序表置为空表
/* 初始条件:顺序线性表L已存在。操作结果:若L为空表,则返回TRUE,否则返回FALSE */
Status ListEmpty(SqList L)
{
if(L.length==0)
return TRUE;
else
return FALSE;
}-
计算顺序表中的元素个数
/* 初始条件:顺序线性表L已存在。操作结果:返回L中数据元素个数 */
int ListLength(SqList L)
{
return L.length;
}-
取出顺序表中的对应位置元素
/* 初始条件:顺序线性表L已存在,1≤i≤ListLength(L) */
/* 操作结果:用e返回L中第i个数据元素的值,注意i是指位置,第1个位置的数组是从0开始 */
Status GetElem(SqList L,int i,ElemType *e)
{
if(L.length==0 || i<1 || i>L.length)
return ERROR;
*e=L.data[i-1];
return OK;
}-
取出对应数值的位序
/* 初始条件:顺序线性表L已存在 */
/* 操作结果:返回L中第1个与e满足关系的数据元素的位序。 */
/* 若这样的数据元素不存在,则返回值为0 */
int LocateElem(SqList L,ElemType e)
{
int i;
if (L.length==0)
return 0;
for(i=0;i<L.length;i++)
{
if (L.data[i]==e)
break;
}
if(i>=L.length)
return 0;
return i+1;
}-
在对应位置插入元素
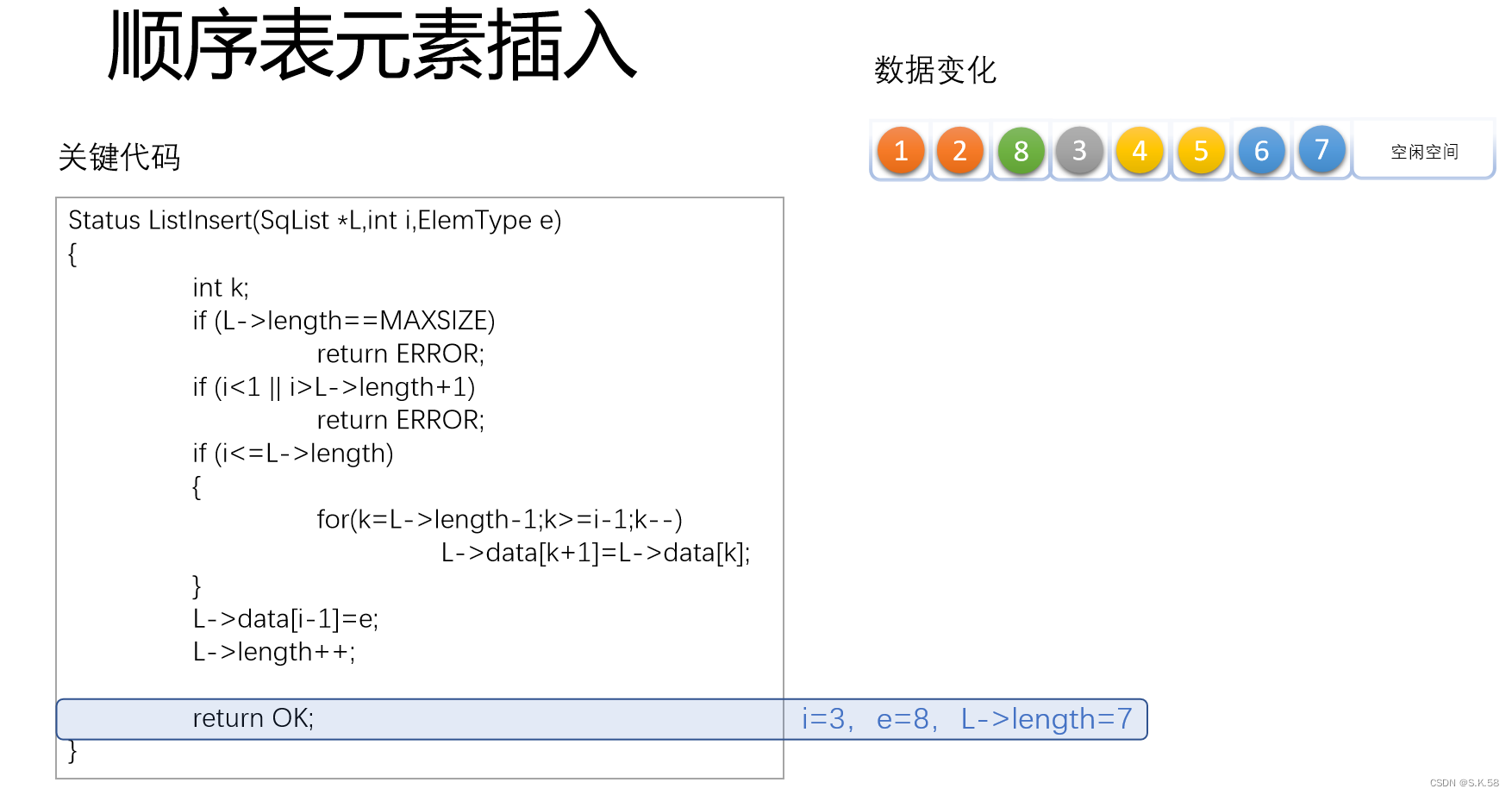
第一步先是判断完顺序表的状态是否是满的,插入位置是否合法
第二步判断是否在表尾,在表尾就直接插入,不在表尾需要将原来位置的数据向后移动一位然后再把数据插入
/* 初始条件:顺序线性表L已存在,1≤i≤ListLength(L), */
/* 操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1 */
Status ListInsert(SqList *L,int i,ElemType e)
{
int k;
if (L->length==MAXSIZE) /* 顺序线性表已经满 */
return ERROR;
if (i<1 || i>L->length+1)/* 当i比第一位置小或者比最后一位置后一位置还要大时 */
return ERROR;
if (i<=L->length) /* 若插入数据位置不在表尾 */
{
for(k=L->length-1;k>=i-1;k--) /* 将要插入位置之后的数据元素向后移动一位 */
L->data[k+1]=L->data[k];
}
L->data[i-1]=e; /* 将新元素插入 */
L->length++;
return OK;
} 

-
将对应位置的元素删除
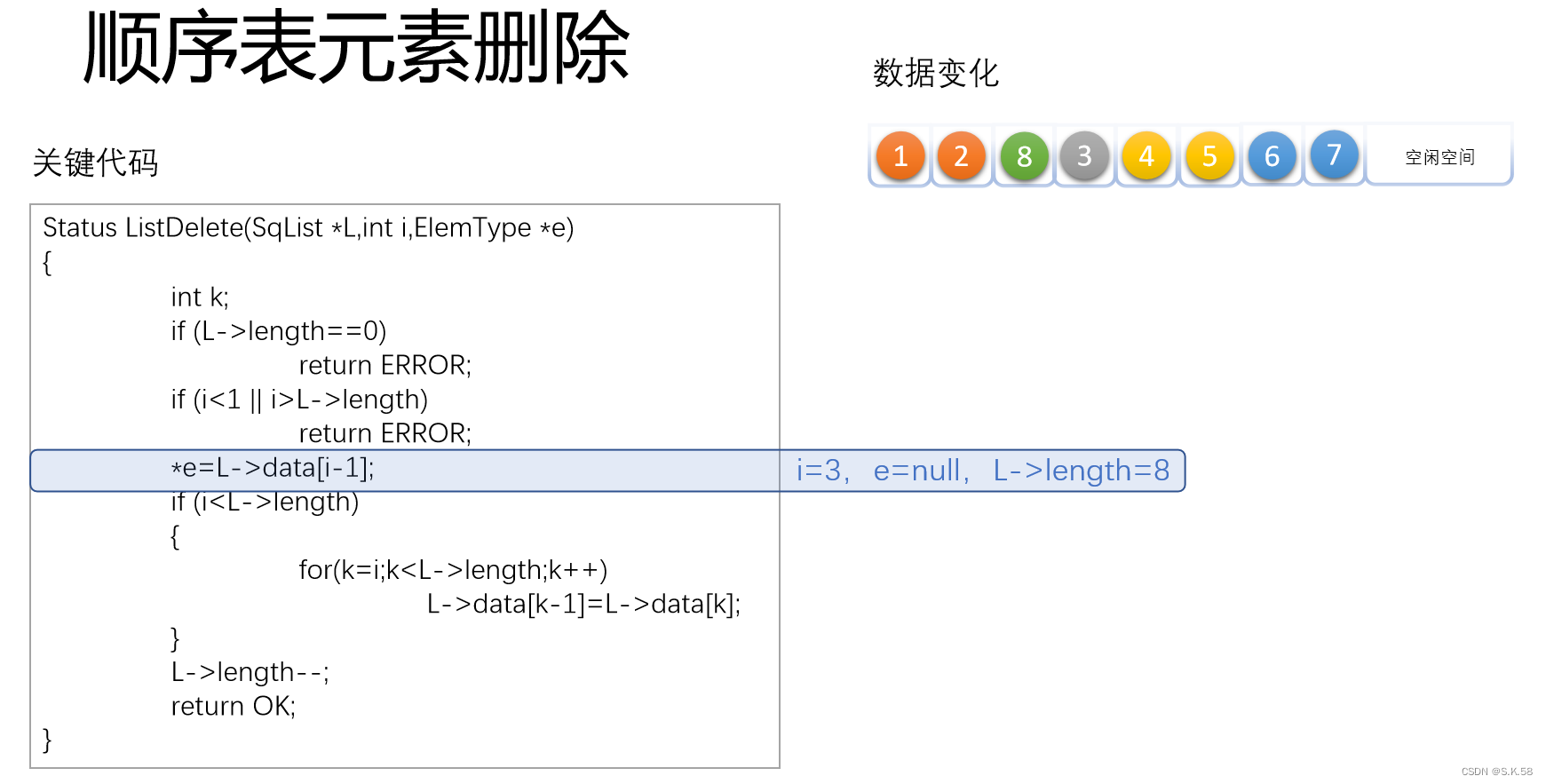
第一步也是先判断顺序表状态
第二步把后面的数据往前移动进行数据覆盖,我们不能直接对内存中的数据进行操作,只能将后面的数据进行覆盖
/* 初始条件:顺序线性表L已存在,1≤i≤ListLength(L) */
/* 操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减1 */
Status ListDelete(SqList *L,int i,ElemType *e)
{
int k;
if (L->length==0) /* 线性表为空 */
return ERROR;
if (i<1 || i>L->length) /* 删除位置不正确 */
return ERROR;
*e=L->data[i-1];
if (i<L->length) /* 如果删除不是最后位置 */
{
for(k=i;k<L->length;k++)/* 将删除位置后继元素前移 */
L->data[k-1]=L->data[k];
}
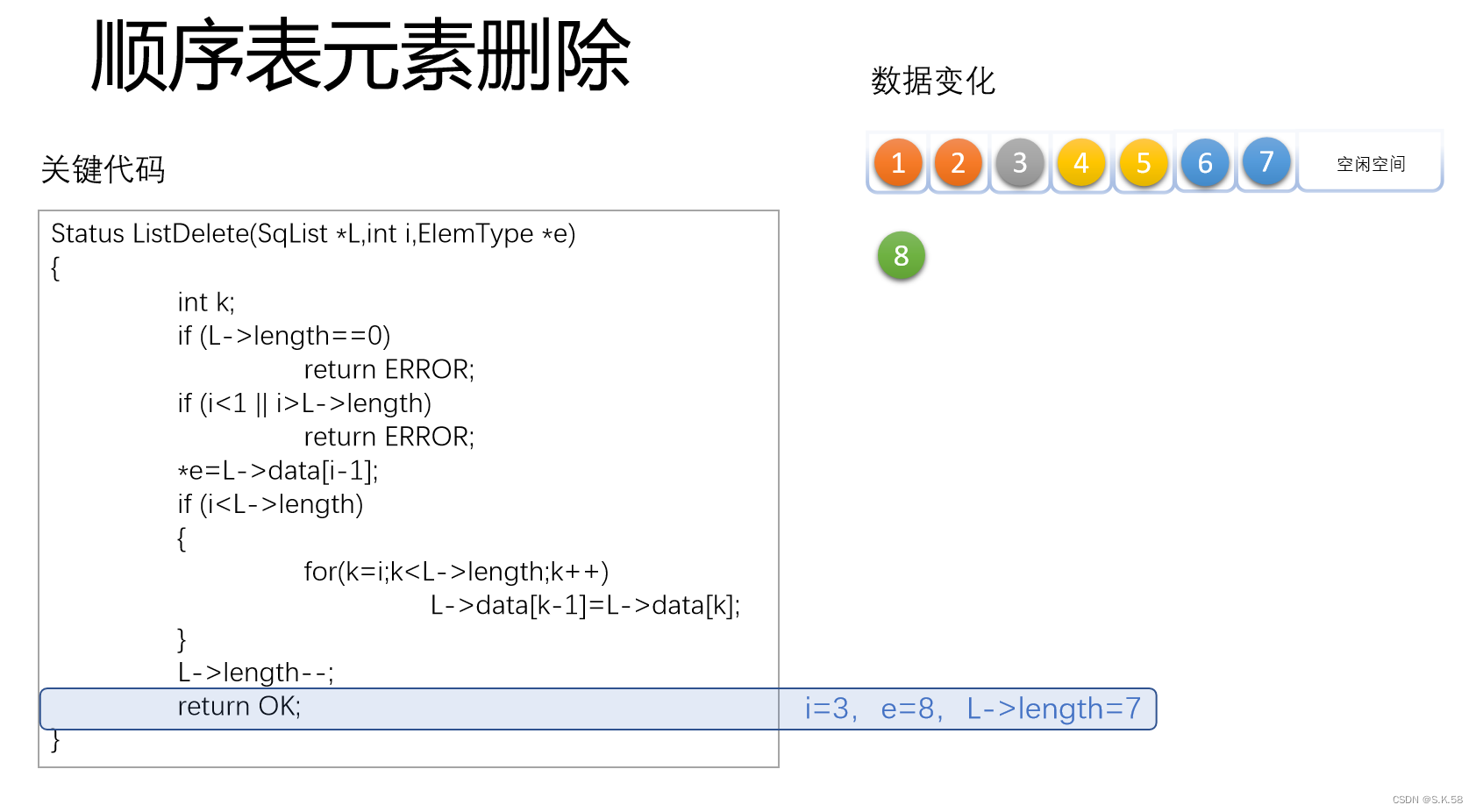
L->length--;
return OK;
}
-
将顺序表中的数据打印出来
/* 初始条件:顺序线性表L已存在 */
/* 操作结果:依次对L的每个数据元素输出 */
Status ListTraverse(SqList L)
{
int i;
for(i=0;i<L.length;i++)
visit(L.data[i]);
printf("\n");
return OK;
}-
将顺序表A和B进行合并
/*将所有的在线性表Lb中但不在La中的数据元素插入到La中*/
void unionL(SqList *La,SqList Lb)
{
int La_len,Lb_len,i;
ElemType e; /*声明与La和Lb相同的数据元素e*/
La_len=ListLength(*La); /*求线性表的长度 */
Lb_len=ListLength(Lb);
for (i=1;i<=Lb_len;i++)
{
GetElem(Lb,i,&e); /*取Lb中第i个数据元素赋给e*/
if (!LocateElem(*La,e)) /*La中不存在和e相同数据元素*/
ListInsert(La,++La_len,e); /*插入*/
}
}总结
本次对数据结构中的顺序表进行讲解,前路还有很远,给我坚持住了