二叉树

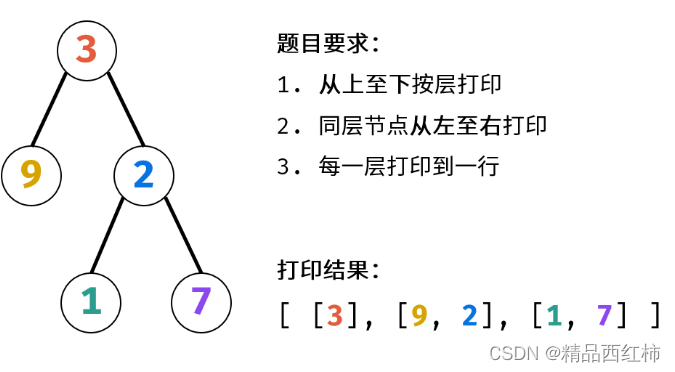
1.二叉树的层序遍历

二叉树的层序遍历
二叉树的层序遍历可以用先进先出的队列来实现。
将每一层的所有node都添加到队列中，记录下当前队列的长度，即该层的元素数量；
遍历队列中当前层的元素，添加该层每一个元素的左右子树。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> q;
        vector<vector<int>> ans;
        if (root == nullptr) return ans;
        q.push(root);
        while (!q.empty()) {
            int n = q.size();
            vector<int> v;
            while (n--) {
                auto tmp = q.front();
                q.pop();
                v.push_back(tmp->val);
                if (tmp->left) q.push(tmp->left);
                if (tmp->right) q.push(tmp->right);
            }
            ans.push_back(v);
        }
        return ans;
    }
};

2.验证二叉搜索树

验证二叉搜索树
如果该二叉树的左子树不为空，则左子树上所有节点的值均小于它的根节点的值； 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；它的左右子树也为二叉搜索树。
不能单纯的比较左节点小于中间节点，右节点大于中间节点，比如我写出了类似这样的代码：

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        if (root == nullptr) return true;
        if (root->left == nullptr || root->right == nullptr) return false;
        if (root->val <= root->left->val || root->val >= root->right->val) return false;
        return (isValidBST(root->left) && isValidBST(root->right));
    }
};

我们要比较的是 左子树所有节点小于中间节点，右子树所有节点大于中间节点。所以以上代码的判断逻辑是错误的。

例如： [10,5,15,null,null,6,20] 这个case：

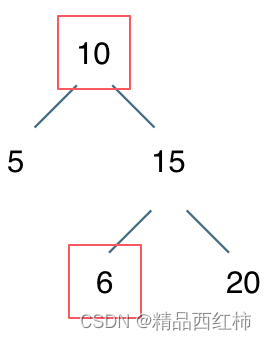
节点10大于左节点5，小于右节点15，但右子树里出现了一个6 这就不符合了！
方法一，辅助函数：
这启示我们设计一个递归函数 bfs(TreeNode* root, long long max, long long min) 来递归判断，函数表示考虑以 root 为根的子树，判断子树中所有节点的值是否都在 (l,r) 的范围内（注意是开区间）。如果 root 节点的值 val 不在 (l,r) 的范围内说明不满足条件直接返回，否则我们要继续递归调用检查它的左右子树是否满足，如果都满足才说明这是一棵二叉搜索树。
注意这里的 long long 和 LONG_MAX/LONG_MIN

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool bfs(TreeNode* root, long long max, long long min) {
        if (root == nullptr) return true;
        if (root->val >= max || root->val <= min) return false;
        return (bfs(root->left, root->val, min) && bfs(root->right, max, root->val));
    }
    bool isValidBST(TreeNode* root) {
        if (root == nullptr) return true;
        return bfs(root, LONG_MAX, LONG_MIN);
    }
};

方法二，中序遍历
二叉搜索树的中序遍历以后得到的序列一定是升序序列
中序遍历时，判断当前节点是否大于中序遍历的前一个节点，如果大于，说明满足 BST，继续遍历；否则直接返回 false。

/*
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    long pre = LONG_MIN;
    bool isValidBST(TreeNode* root) {
        if (root == nullptr) return true;
        //先访问左子树
        bool left = isValidBST(root->left);
        //判断当前节点是否大于前一个节点
        if (root->val <= pre) return false;
        pre = root->val;
        //访问右子树
        bool right = isValidBST(root->right);
        return left && right;
    }
};

3.二叉树的右视图

二叉树的右视图
题目结果可以用二叉树的层序遍历来实现，每次只留下每一层最右侧的值，就比较简单啦

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        vector<int> ans;
        if (root == nullptr) return ans;
        queue<TreeNode*> q;
        q.push(root);
        while (!q.empty()) {
            int n = q.size();
            TreeNode* tmp = nullptr;
            while (n--) {
                tmp = q.front();
                q.pop();
                if (tmp->left) q.push(tmp->left);
                if (tmp->right) q.push(tmp->right);
            }
            ans.push_back(tmp->val);
        }
        return ans;
    }
};