知识回顾:
寻址:
其中,比例因子S,只能是1,2,4,8中的数,这是因为在LEA的独立电路中使用移位寄存器
上节课的补充:
mov部分:
mov value , %eax
mov $value , %eax第一条指令,把value的值赋值给寄存器eax
第二条指令,把立即数(value的地址)赋值给寄存器eax
如下图所示 
lea指令
lea(load effective address),LEA指令的功能是取偏移地址, 指令形式是从存储器读数据到寄存器, 效果是将存储器的有效地址写入到目的操作数。只是取地址而不是取地址中的数据
lea 指令是mov 指令的变形,lea 指令形式看上去是从存储器读数据到寄存器,但实际并没有引用存储器,而是将有效地址写入目的操作数(必须是寄存器)
类似于C语言中的&
leal S,D 表示 D <- &S有与其等效的mov指令
mov $S , D作用:
- 地址计算/地址传送
- 执行简单的算术操作
地址计算/地址传送练习
若寄存器%edx 的值为x,那么
leal 7(%edx,%edx,4),%eax表示:寄存器%eax的值为5x+7
leal 8(%edi), %eax表示:%eax+8 -> %eax
movl 8(%edi), %eax表示:%edi+8 -> %eax
演示:1012.s


执行简单的算术操作
对于下面的程序
int scale(int x,int y,int z)
{
int t=8*x+2*y+5*z;
return t;
}反汇编代码如下,令%esi=x,%edi=y,%edx=z,%eax=t
scale
leal (%edx,%edi,4) %eax
leal (%eax,%edi,2) %eax
leal (%eax,%esi,8) %eax
ret注意:
比例因子只能是1,2,4,8,在LEA的独立电路中用移位寄存器可以简单高效地实现此类计算!
新知识
函数的栈帧
每一个函数或过程在执行时,都需要在内存中分配一个空间来保存运行时数据,这个空间由于是采用栈的方式进行操作,所以也称为栈帧。
栈是向下增长的。上面大,下面小。存取地址从大向小的存。如图所示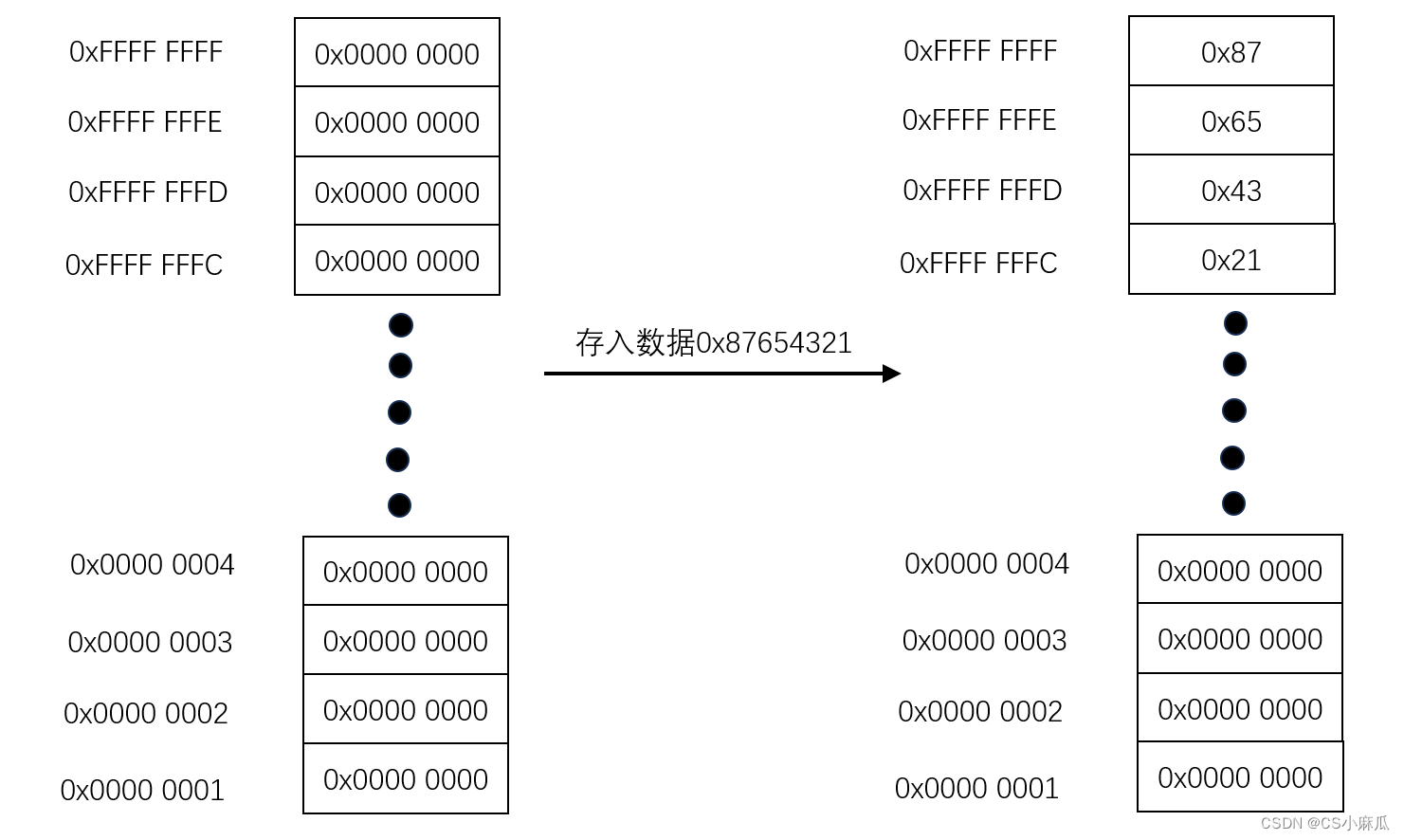
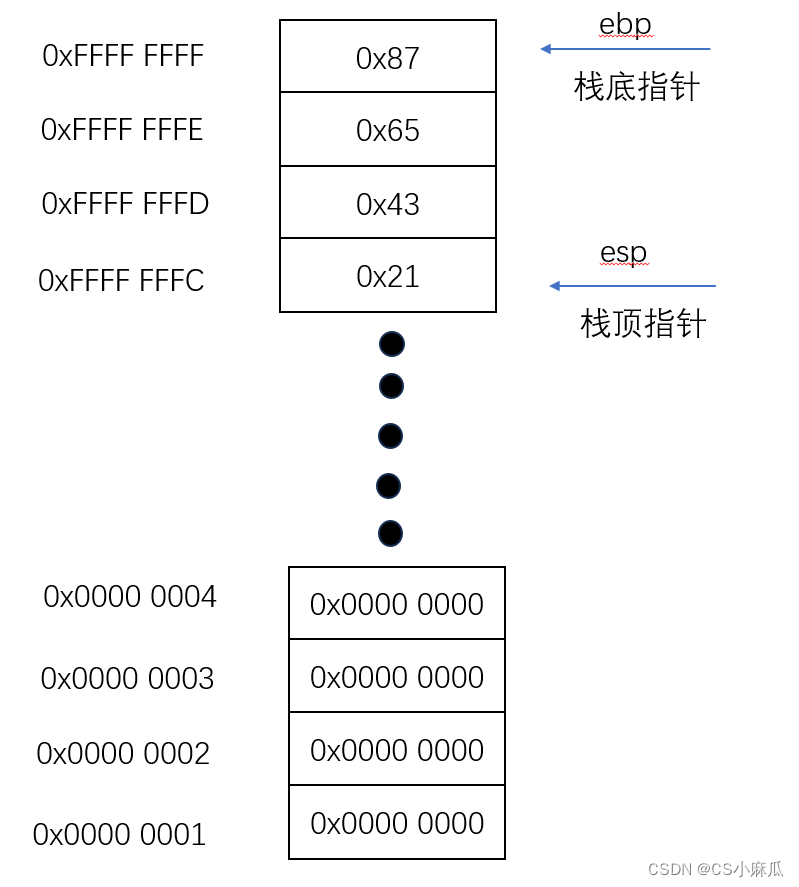
栈底的位置存储在寄存器%ebp中,栈顶的位置存储在寄存器%esp中
esp指向的位置存储的什么不知道,因为不知道之前栈中存储的是什么数据,但是我们可以通过命令查看当中的数据
栈是向“下”增长的,或者说是向地址0x0处增加的,因此%esp中的值小于或等于%ebp中的值。
如图所示
注意:
栈帧是内存中一段连续的内存空间,被调用者的栈帧紧挨着调用者的栈帧
每个函数,在同一时刻只会有一个活跃栈帧
栈顶是朝着低地址方向(栈是向着零地址方向增长)如图所示

栈操作
栈有两个基本的操作:
- 入栈:将一个新的元素放到栈顶。push
- 出栈:从栈顶取出一个元素。pop
栈顶的元素总是最后入栈,需要出栈时,又最先被从栈中取出。
栈的操作规则:后进先出
栈顶指针:保存在%esp寄存器中,当栈为空的时候,%esp指向最高地址空间的下一位
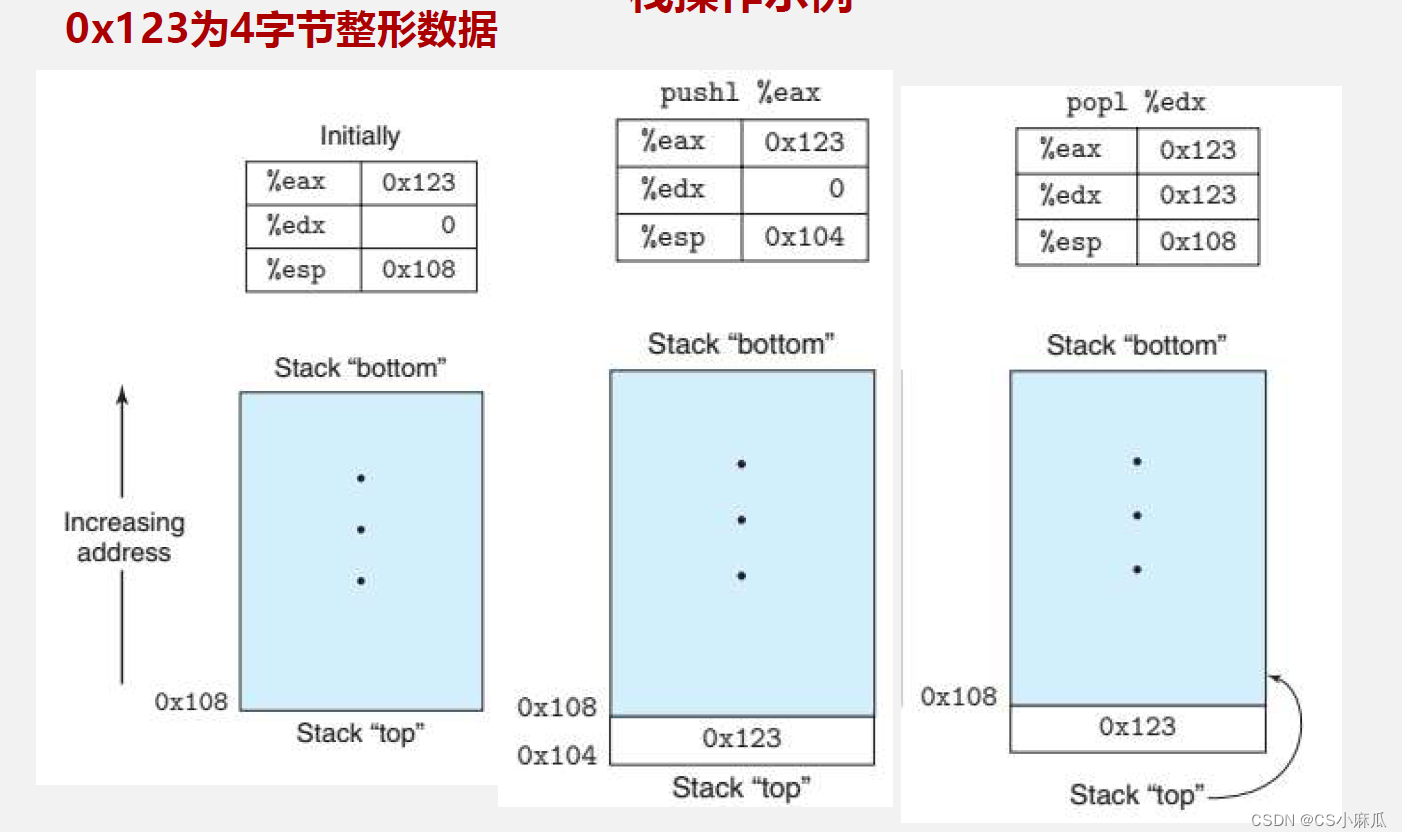
入栈:
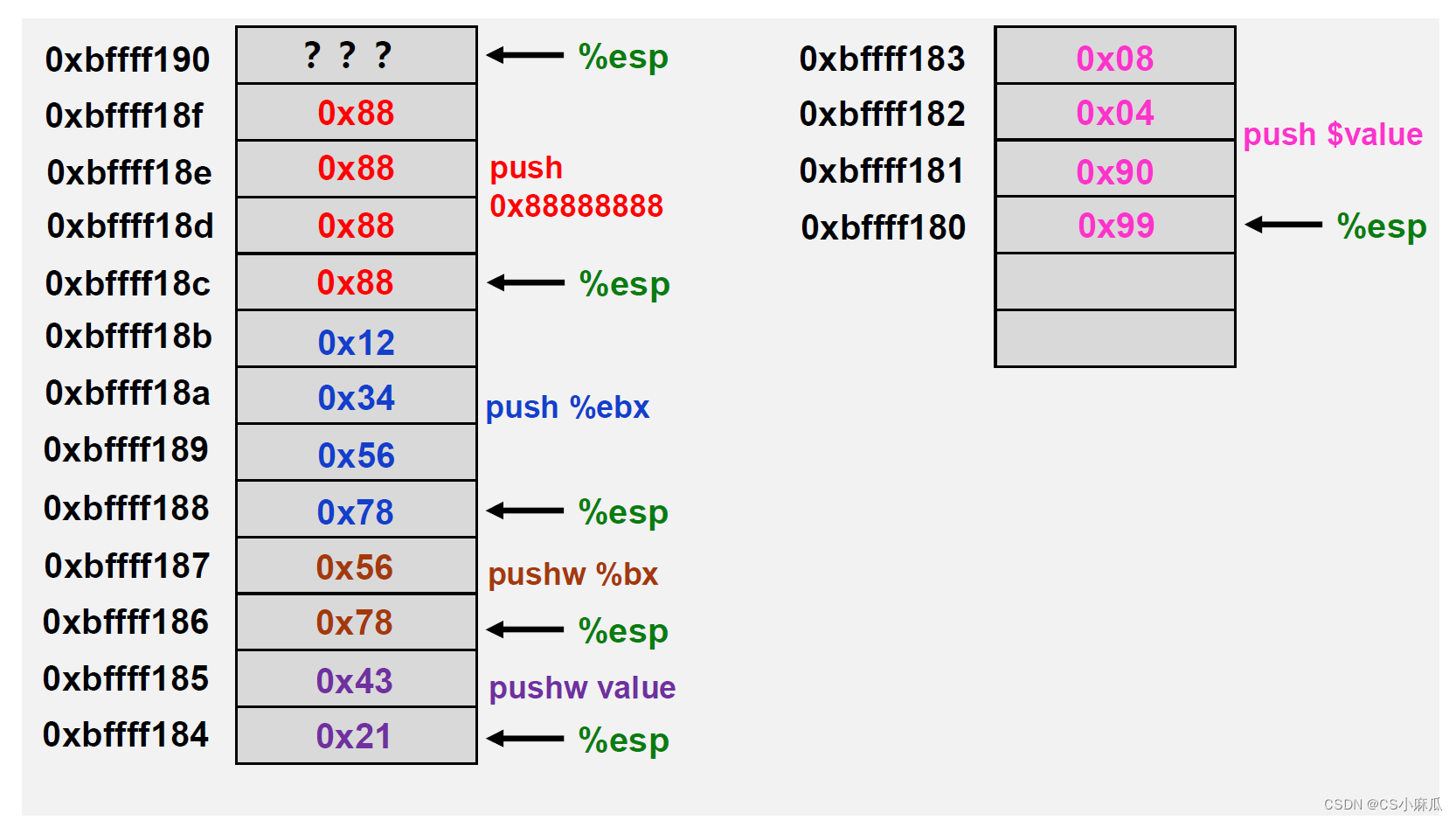
push操作只有目的操作数,没有源操作数。在每个程序所分配的内存中,划分出一段连续的区域,作为栈空间。示例1013.s
push申请对应的源寄存器的数据长度,esp减小相应字节数(即%esp-n)因为存储的数据按照小端法存储,低位数据在栈顶位置
例一如图所示:
先将0x8888 8888压入栈中,再压入%ebx(对应的为pushl,4个内存单元),再压入%bx(对应两个内存单元),在压入0x4321(value),最后压入value的地址
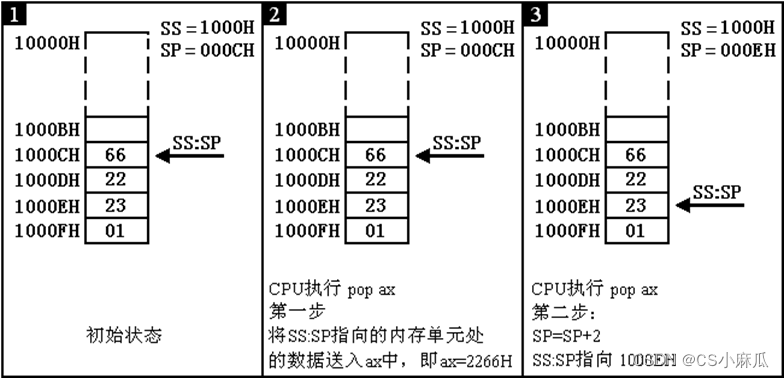
例二在执行push ax指令时,主要做了一下2件事
- 先将SP=SP–2。
- 将ax中的内容送入SS:SP指向的内存单元处,SS:SP此时指向新栈顶。
注意:
push $value 把value的首地址放到栈里
pushw $value 只把低两位地址放到栈里
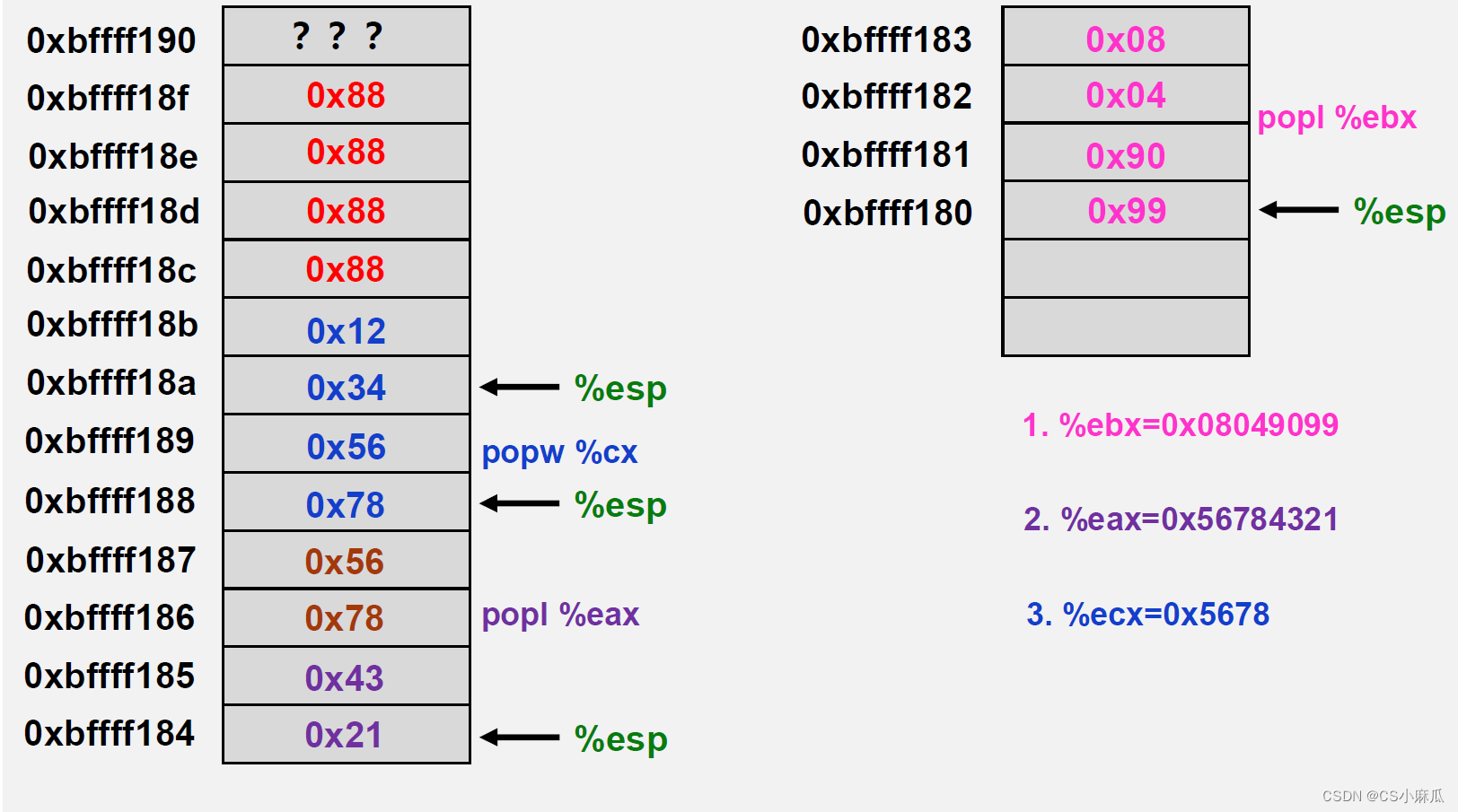
出栈
pop后数据依然在原来位置但是是无效的
pop使用方法与push类似
如图所示:
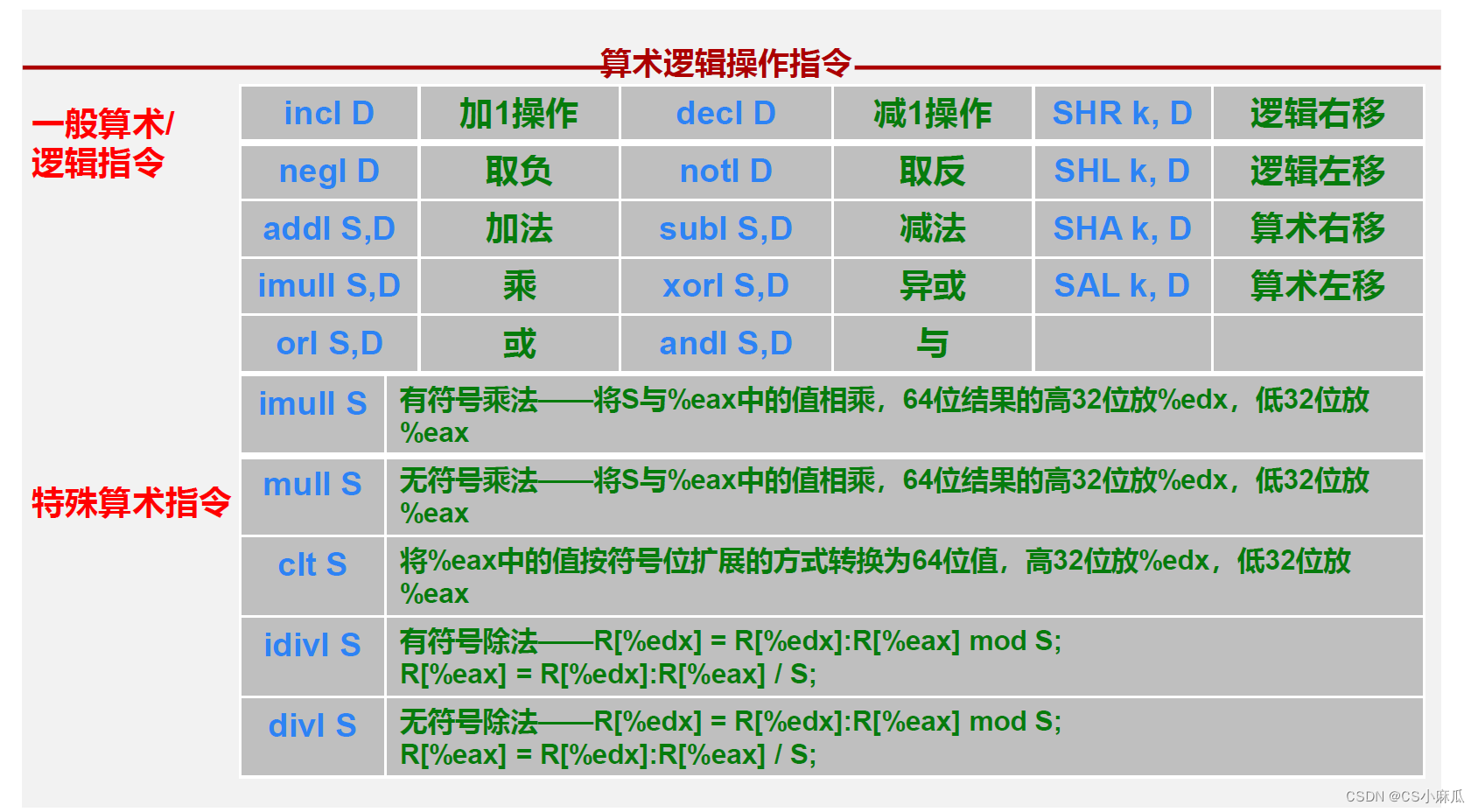
逻辑算术指令
指令集如图所示
跳转指令
寄存器eip 存放下一条要执行指令的地址

无条件跳转:jmp
jmp指令。条件执行通常涉及将控制转移到不跟随当前正在执行的指令的指令的地址。 控制权的转移可以是向前的,以执行一组新的指令,也可以是向后的,以重新执行相同的步骤。更多请看教材128页
语法:
JMP 指令提供了一个标签名称,其中控制流立即转移。
jmp label程序:1014.s提供相应测试代码
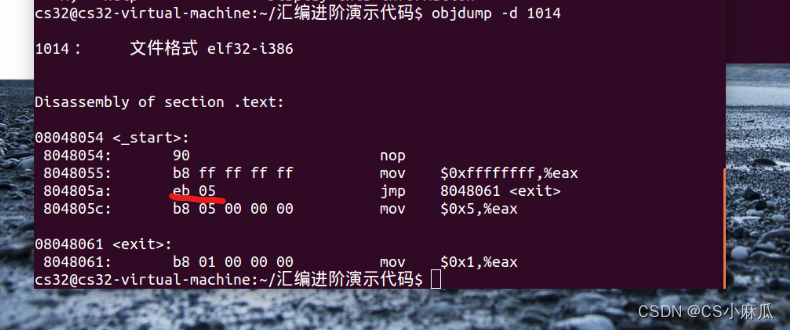
如图标记处,这里的05,是将指下一条指令(mov $5, %eax)的地址(即当前PC所存地址)
再加上05,就能得到跳转目的地<exit>的地址
条件跳转:jg
如果条件跳转中满足某个指定条件,则控制流转移到目标指令。 根据条件和数据,有许多条件跳转指令。条件跳转按照%eflags中的值来判断是否该跳转。 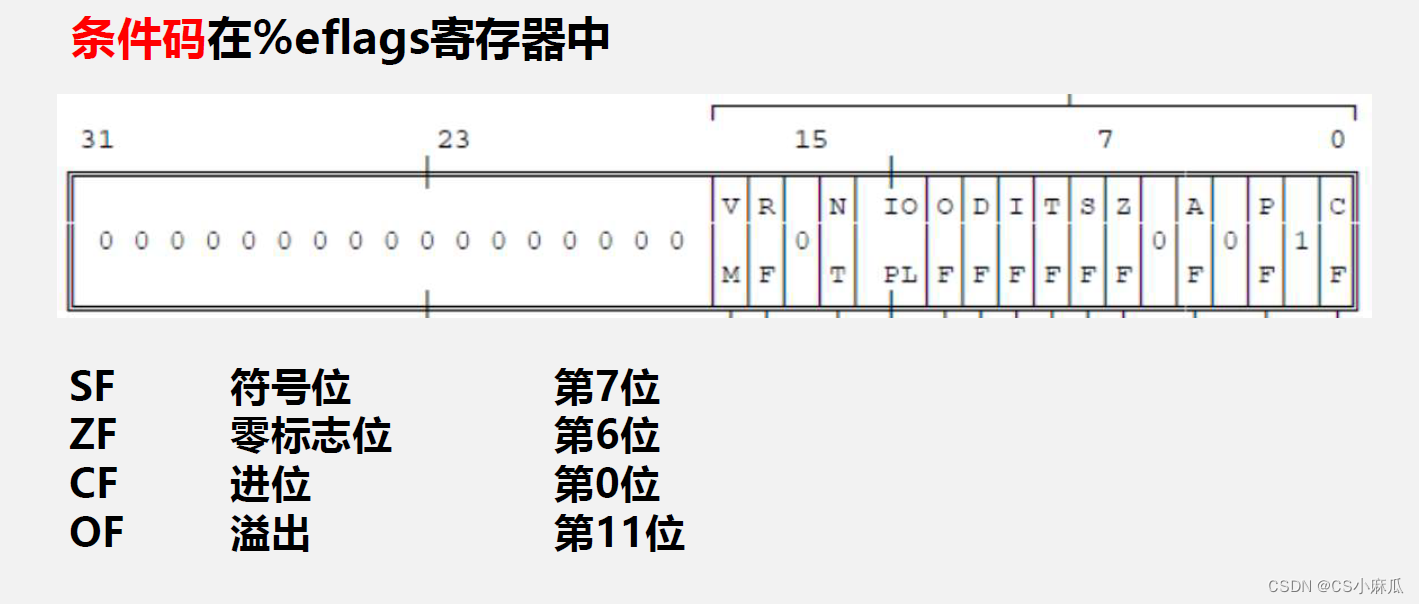
可以参考另一篇博客:Linux汇编入门大杂烩上!-CSDN博客