Restormer: Efficient Transformer for High-Resolution Image Restoration

Abstract

由于卷积神经网络（CNN）在从大规模数据中学习可概括的图像先验方面表现良好，因此这些模型已广泛应用于图像恢复和相关任务。最近，另一类神经架构 Transformer 在自然语言和高级视觉任务上表现出了显着的性能提升。虽然 Transformer 模型弥补了 CNN 的缺点（即有限的感受野和对输入内容的不适应性），但其计算复杂度随空间分辨率呈二次方增长，因此无法应用于大多数涉及高分辨率图像的图像恢复任务。在这项工作中，我们通过在构建块（多头注意力和前馈网络）中进行几个关键设计，提出了一种高效的 Transformer 模型，使其可以捕获远程像素交互，同时仍然适用于大图像。我们的模型名为 Restoration Transformer (Restormer)，在多项图像恢复任务上取得了最先进的结果，包括图像去雨、单图像运动去模糊、散焦去模糊（单图像和双像素数据）以及图像去噪（高斯灰度/彩色去噪、真实图像去噪）。源代码和预训练模型可在 https://github.com/swz30/Restormer 获取。

1. Introduction

图像恢复是通过从降级输入中消除降级（例如噪声、模糊、雨滴）来重建高质量图像的任务。由于不适定的性质，这是一个极具挑战性的问题，通常需要强大的图像先验才能进行有效的恢复。由于卷积神经网络（CNN）在从大规模数据中学习可概括的先验方面表现良好，因此与传统的恢复方法相比，它们已成为更好的选择。

CNN 的基本操作是“卷积”，它提供局部连接和平移等方差。虽然这些特性为 CNN 带来了效率和泛化性，但它们也引起了两个主要问题。 (a) 卷积算子的感受野有限，因此无法对远程像素依赖性进行建模。 (b) 卷积滤波器在推理时具有静态权重，因此不能灵活地适应输入内容。为了解决上述缺点，一种更强大、更动态的替代方案是自注意力（SA）机制[17,77,79,95]，它通过所有其他位置的加权和来计算给定像素的响应。

自注意力是 Transformer 模型 [34, 77] 的核心组成部分，但具有独特的实现，即针对并行化和有效表示学习进行优化的多头 SA。 Transformers 在自然语言任务 [10,19,49,62] 和高级视觉问题 [11,17,76,78] 上表现出了最先进的性能。尽管 SA 在捕获长距离像素交互方面非常有效，但其复杂性随空间分辨率呈二次方增长，因此无法应用于高分辨率图像（图像恢复中的常见情况）。最近，为图像恢复任务定制 Transformer 的努力还很少[13,44,80]。为了减少计算负载，这些方法要么在每个像素周围大小为 8×8 的小空间窗口上应用 SA [44, 80]，要么将输入图像划分为大小为 48×48 的非重叠块并在每个块上计算 SA独立地[13]。然而，限制 SA 的空间范围与捕获真实的远程像素关系的目标是矛盾的，尤其是在高分辨率图像上。

在本文中，我们提出了一种用于图像恢复的高效 Transformer，它能够对全局连接进行建模，并且仍然适用于大图像。具体来说，我们引入了一个多 Dconv 头“转置”注意力（MDTA）块（第 3.1 节）来代替具有线性复杂度的普通多头 SA [77]。它跨特征维度而不是空间维度应用 SA，即，MDTA 不是显式地建模成对像素交互，而是计算跨特征通道的互协方差，以从（关键和查询投影）输入特征获取注意力图。我们的 MDTA 块的一个重要特征是在特征协方差计算之前进行局部上下文混合。这是通过使用 1×1 卷积对跨通道上下文进行像素级聚合以及使用高效深度卷积对局部上下文进行通道级聚合来实现的。该策略提供了两个关键优势。首先，它强调空间局部上下文，并在我们的管道中引入卷积运算的互补优势。其次，它确保在计算基于协方差的注意力图时隐式建模像素之间的上下文全局关系。

前馈网络（FN）是 Transformer 模型 [77] 的另一个构建块，它由两个完全连接的层组成，其间具有非线性。在这项工作中，我们用门控机制 [16] 重新表述了常规 FN [77] 的第一个线性变换层，以改善通过网络的信息流。该门控层被设计为两个线性投影层的逐元素乘积，其中一个由 GELU 非线性激活[27]。我们的门控 Dconv FN (GDFN)（第 3.2 节）也基于类似于 MDTA 模块的本地内容混合，以同样强调空间上下文。 GDFN 中的门控机制控制哪些互补特征应向前流动，并允许网络层次结构中的后续层专门关注更精细的图像属性，从而产生高质量的输出。

除了上述架构新颖性之外，我们还展示了 Restormer 渐进式学习策略的有效性（第 3.3 节）。在此过程中，网络在早期 epoch 中接受小补丁和大批量训练，并在后期 epoch 中接受逐渐大的图像补丁和小批量训练。这种训练策略有助于 Restormer 从大图像中学习上下文，并随后在测试时提供质量性能改进。我们进行了全面的实验，并在 16 个基准数据集上展示了 Restormer 的最先进性能，适用于多种图像恢复任务，包括图像去雨、单图像运动去模糊、散焦去模糊（在单图像和双像素数据上）和图像去噪（针对合成数据和真实数据）；参见图 1。此外，我们提供了广泛的消融来显示架构设计和实验选择的有效性。

这项工作的主要贡献总结如下：

• 我们提出了Restormer，一种编码器-解码器Transformer，用于在高分辨率图像上进行多尺度局部-全局表示学习，而不将它们分解到局部窗口中，从而利用遥远的图像上下文。

• 我们提出了一个多Dconv 头转置注意（MDTA）模块，它能够聚合局部和非局部像素交互，并且足够有效地处理高分辨率图像。

• 一种新的门控Dconv前馈网络（GDFN），它执行受控特征转换，即抑制信息量较少的特征，并仅允许有用的信息进一步通过网络层次结构。

2. Background

Image Restoration.

近年来，数据驱动的 CNN 架构 [7,18,92,93,105,107] 已被证明优于传统的恢复方法 [26,36,53,75]。在卷积设计中，基于编码器-解码器的 UNet 架构 [3,14,39,80,90,93,99] 由于其分层多尺度表示同时保持计算效率而被主要研究用于恢复。类似地，由于特别关注学习残差信号，基于跳跃连接的方法已被证明对于恢复是有效的[24,48,92,106]。空间和通道注意模块也被纳入以选择性地关注相关信息[43,92,93]。我们建议读者参考 NTIRE 挑战报告 [2,5,30,57] 和最近的文献综述 [8,42,73]，其中总结了图像恢复的主要设计选择。

Vision Transformers.

Transformer 模型最初是为自然语言任务中的序列处理而开发的[77]。它已适用于许多视觉任务，例如图像识别[17,76,88]、分割[78,83,108]、对象检测[11,50,109]。视觉变换器 [17, 76] 将图像分解为一系列补丁（局部窗口）并学习它们的相互关系。这些模型的显着特征是学习图像块序列之间的远程依赖性的强大能力以及对给定输入内容的适应性[34]。由于这些特性，Transformer 模型也被研究用于低级视觉问题，例如超分辨率 [44,85]、图像着色 [37]、去噪 [13, 80] 和去雨 [80]。然而，Transformers 中 SA 的计算复杂度会随着图像块的数量呈二次方增加，从而阻碍了其在高分辨率图像中的应用。因此，在需要生成高分辨率输出的低级图像处理应用中，最近的方法通常采用不同的策略来降低复杂性。一种潜在的补救措施是使用 Swin Transformer 设计 [44] 在局部图像区域 [44, 80] 中应用自注意力。然而，这种设计选择限制了局部邻域内的上下文聚合，违背了在卷积上使用自注意力的主要动机，因此不太适合图像恢复任务。相比之下，我们提出了一个 Transformer 模型，它可以学习远程依赖关系，同时保持计算效率。

3. Method

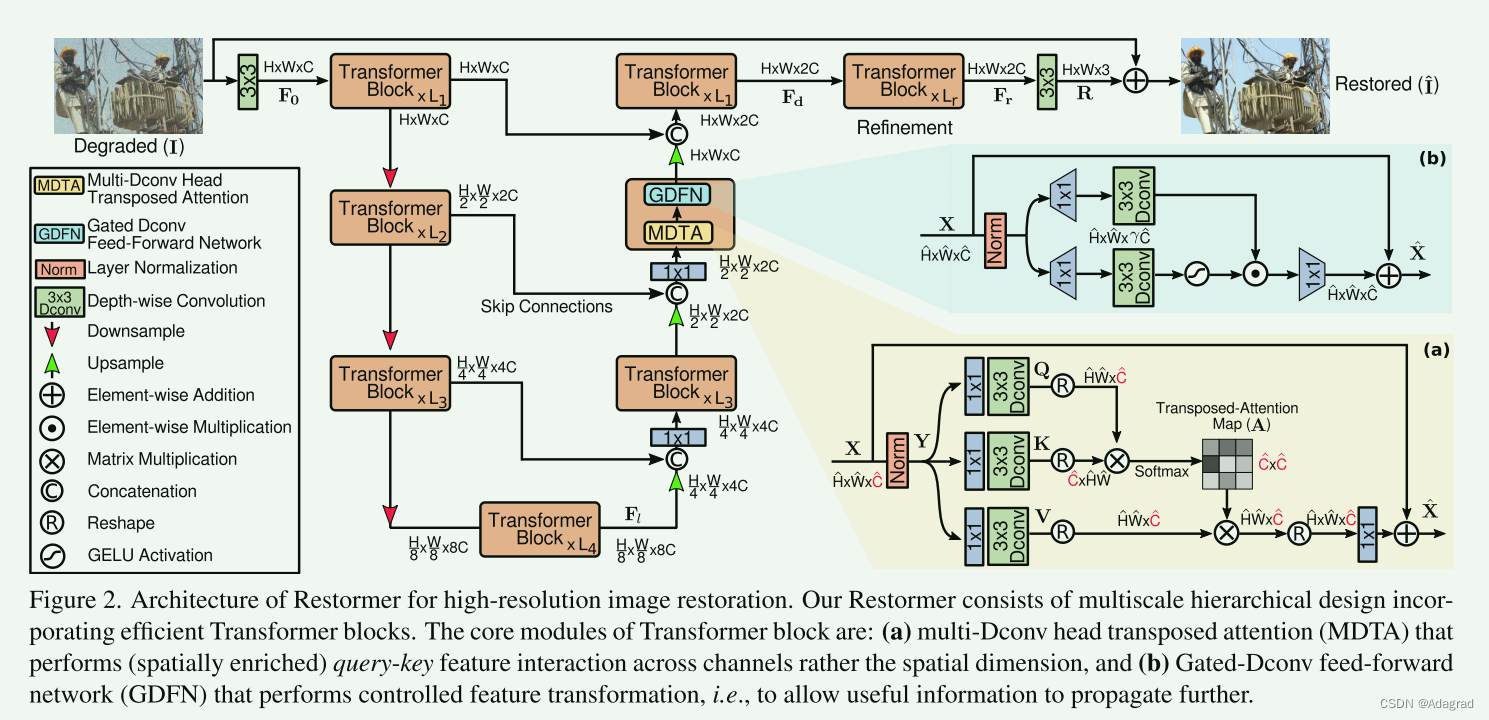
我们的主要目标是开发一种高效的 Transformer 模型，可以处理用于恢复任务的高分辨率图像。为了缓解计算瓶颈，我们在多头 SA 层和多尺度分层模块中引入了关键设计，该模块的计算要求比单尺度网络[44]更少。我们首先展示 Restormer 架构的整体流程（见图 2）。然后我们描述了所提出的 Transformer 块的核心组件：（a）多 Dconv 头转置注意力（MDTA）和（b）门控 Dconv 前馈网络（GDFN）。最后，我们提供了有关有效学习图像统计的渐进式训练方案的详细信息。

Overall Pipeline.

给定一个退化图像 I ∈ RH×W×3，Restormer 首先应用卷积来获得低级特征嵌入 F0 ∈RH×W×C；其中H×W表示空间维度，C是通道数。接下来，这些浅层特征 F0 经过 4 级对称编码器-解码器并转换为深层特征 Fd ∈ RH×W×2C。每个级别的编码器-解码器包含多个 Transformer 块，其中块的数量从上到下逐渐增加以保持效率。从高分辨率输入开始，编码器分层减小空间尺寸，同时扩展通道容量。解码器采用低分辨率潜在特征 Fl ∈ R H 8 ×W 8 ×8C 作为输入，并逐步恢复高分辨率表示。对于特征下采样和上采样，我们分别应用像素不洗牌和像素洗牌操作[69]。为了协助恢复过程，编码器特征通过跳跃连接与解码器特征连接[66]。级联操作之后是 1×1 卷积，以减少除顶部通道之外的所有级别的通道（减半）。在第 1 级，我们让 Transformer 块将编码器的低级图像特征与解码器的高级特征聚合。它有利于保留恢复图像中的精细结构和纹理细节。接下来，深层特征 Fd 在高空间分辨率下的细化阶段进一步丰富。正如我们将在实验部分（第 4 节）中看到的那样，这些设计选择带来了质量改进。最后，对细化后的特征应用卷积层，生成残差图像 R ∈ RH×W×3，将退化图像添加到残差图像中，得到恢复图像：ˆI = I +R。接下来，我们介绍 Transformer 块的模块。

3.1. Multi-Dconv Head Transposed Attention

Transformer 中的主要计算开销来自自注意力层。在传统的 SA [17, 77] 中，键查询点积交互的时间和内存复杂度随着输入的空间分辨率呈二次方增长，即对于 W×H 像素的图像，O(W2H2)。因此，在大多数涉及高分辨率图像的图像恢复任务中应用SA是不可行的。为了缓解这个问题，我们提出了具有线性复杂度的MDTA，如图2（a）所示。关键要素是跨通道而不是空间维度应用 SA，即计算跨通道的互协方差，以生成隐式编码全局上下文的注意力图。作为 MDTA 的另一个重要组成部分，我们引入深度卷积来强调局部上下文，然后再计算特征协方差以生成全局注意力图。

3.2. Gated-Dconv Feed-Forward Network

为了转换特征，常规前馈网络（FN）[17,77]对每个像素位置分别且相同地进行操作。它使用两个 1×1 卷积，一个用于扩展特征通道（通常通过因子 γ=4），第二个用于将通道减少回原始输入维度。在隐藏层中应用非线性。在这项工作中，我们提出了对 FN 的两个基本修改来改进表示学习：(1) 门控机制，(2) 深度卷积。我们的 GDFN 的架构如图 2（b）所示。门控机制被表述为线性变换层两个平行路径的逐元素乘积，其中之一通过 GELU 非线性激活[27]。与 MDTA 一样，我们还在 GDFN 中包含深度卷积，以对空间相邻像素位置的信息进行编码，这对于学习局部图像结构以实现有效恢复非常有用。给定一个输入张量 X ∈ $R^{\hat{H}\hat{W}\times\hat{H}\hat{W}}$ ，GDFN 的公式为：

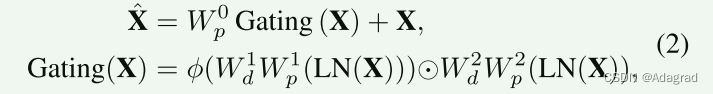
其中 $\odot$ 表示逐元素乘法，φ表示GELU非线性，LN是层归一化[9]。总体而言，GDFN 控制着我们管道中各个层级的信息流，从而允许每个级别专注于与其他级别互补的细节。也就是说，与 MDTA（专注于利用上下文信息丰富特征）相比，GDFN 提供了独特的作用。由于与常规 FN [17] 相比，所提出的 GDFN 执行更多操作，因此我们降低了扩展率 γ，以便具有相似的参数和计算负担。

3.3. Progressive Learning

基于 CNN 的恢复模型通常在固定大小的图像块上进行训练。然而，在小裁剪补丁上训练 Transformer 模型可能不会对全局图像统计数据进行编码，从而在测试时在全分辨率图像上提供次优性能。为此，我们进行渐进式学习，其中网络在早期训练时期在较小的图像块上进行训练，在后期训练时期在逐渐增大的图像块上进行训练。通过渐进式学习在混合大小的补丁上训练的模型在测试时表现出增强的性能，其中图像可以具有不同的分辨率（图像恢复中的常见情况）。渐进式学习策略的行为方式与课程学习过程类似，其中网络从更简单的任务开始，逐渐转向学习更复杂的任务（需要保留精细图像结构/纹理）。由于对大补丁的训练需要更长的时间，因此我们随着补丁大小的增加而减少批量大小，以保持每个优化步骤与固定补丁训练的时间相似。

4. Experiments and Analysis

我们在基准数据集和四个图像处理任务的实验设置上评估了所提出的 Restormer：（a）图像去雨，（b）单图像运动去模糊，（c）散焦去模糊（在单图像和双像素数据上），以及（ d) 图像去噪（针对合成数据和真实数据）。补充材料中提供了有关数据集、训练协议和其他视觉结果的更多详细信息。在表格中，所评估方法的最佳和次佳质量分数被突出显示并带有下划线。

Implementation Details.

我们为不同的图像恢复任务训练单独的模型。在所有实验中，除非另有说明，我们使用以下训练参数。我们的 Restormer 采用 4 级编码器-解码器。从level-1到level-4，Transformer块的数量为[4,6,6,8]，MDTA中的注意力头为[1,2,4,8]，通道数量为[48,96, 192、384]。细化阶段包含 4 个块。 GDFN中的通道扩展因子是γ=2.66。我们使用 AdamW 优化器（β1=0.9，β2=0.999，权重衰减 1e−4）和 L1 损失训练模型进行 300K 次迭代，初始学习率 3e−4 通过余弦退火逐渐降低到 1e−6 [51]。对于渐进式学习，我们开始使用补丁大小 128×128 和批量大小 64 进行训练。补丁大小和批量大小对更新为 [(1602,40), (1922,32), (2562,16), (3202, 8), (3842,8)] 迭代 [92K, 156K, 204K, 240K, 276K]。对于数据增强，我们使用水平和垂直翻转

4.1. Image Deraining Results

4.2. Single-image Motion Deblurring Results

4.3. Defocus Deblurring Results

4.4. Image Denoising Results

4.5. Ablation Studies

对于消融实验，我们仅在大小为 128×128 的图像块上训练高斯颜色去噪模型，进行 100K 次迭代。在 Urban100 [29] 上进行测试，并针对具有挑战性的噪声水平 σ=50 进行分析。 FLOP 和推理时间是根据图像大小 256×256 计算的。表 7-10 显示我们的贡献带来了质量性能改进。接下来，我们分别描述每个组件的影响。

Improvements in multi-head attention.

表 7c 表明，我们的 MDTA 比基线（表 7a）提供了 0.32 dB 的有利增益。此外，通过深度卷积将局部性引入 MDTA 可以提高鲁棒性，因为删除局部性会导致 PSNR 下降（参见表 7b）。

Improvements in feed-forward network (FN)

表 7d 显示 FN 中控制信息流的门控机制比传统 FN [77] 产生 0.12 dB 增益。与多头注意力一样，在 FN 中引入局部机制也带来了性能优势（见表 7e）。我们通过结合门控深度卷积进一步增强 FN。对于噪声水平 50，我们的 GDFN（表 7f）实现了比标准 FN [77] 0.26 dB 的 PSNR 增益。总体而言，我们的 Transformer 模块的贡献导致比基线显着增益 0.51 dB。

Design choices for decoder at level-1

为了将编码器特征与级别 1 的解码器聚合，我们在串联操作后不使用 1×1 卷积（将通道减少一半）。它有助于保留来自编码器的精细纹理细节，如表 8 所示。这些结果进一步证明了在细化阶段添加 Transformer 块的有效性。

Impact of progressive learning.

表 9 显示，渐进式学习提供了比固定补丁训练更好的结果，同时训练时间相似。

Deeper or wider Restormer?

表 10 显示，在相似的参数/FLOPs 预算下，深窄模型比宽浅模型的性能更准确。然而，由于并行化，更宽的模型运行得更快。在本文中，我们使用深窄 Restormer。

5. Conclusion

我们提出了一种图像恢复 Transformer 模型 Restormer，它在处理高分辨率图像方面具有计算效率。我们为 Transformer 模块的核心组件引入了关键设计，以改进特征聚合和转换。具体来说，我们的 multiDconv 头部转置注意力（MDTA）模块通过跨通道而不是空间维度应用自注意力来隐式模拟全局上下文，因此具有线性复杂度而不是二次复杂度。此外，所提出的门控 DConv 前馈网络（GDFN）引入了门控机制来执行受控特征转换。为了将 CNN 的优势融入到 Transformer 模型中，MDTA 和 GDFN 模块都包含用于编码空间局部上下文的深度卷积。对 16 个基准数据集的大量实验表明，Restormer 在众多图像恢复任务中实现了最先进的性能。

代码解读

MDTA

##########################################################################
## Multi-DConv Head Transposed Self-Attention (MDTA)
class Attention(nn.Module):
    def __init__(self, dim, num_heads, bias):
        super(Attention, self).__init__()
        self.num_heads = num_heads
        self.temperature = nn.Parameter(torch.ones(num_heads, 1, 1))

        self.qkv = nn.Conv2d(dim, dim*3, kernel_size=1, bias=bias)
        self.qkv_dwconv = nn.Conv2d(dim*3, dim*3, kernel_size=3, stride=1, padding=1, groups=dim*3, bias=bias)
        self.project_out = nn.Conv2d(dim, dim, kernel_size=1, bias=bias)
        


    def forward(self, x):
        b,c,h,w = x.shape

        qkv = self.qkv_dwconv(self.qkv(x))
        q,k,v = qkv.chunk(3, dim=1)   
        
        q = rearrange(q, 'b (head c) h w -> b head c (h w)', head=self.num_heads)
        k = rearrange(k, 'b (head c) h w -> b head c (h w)', head=self.num_heads)
        v = rearrange(v, 'b (head c) h w -> b head c (h w)', head=self.num_heads)

        q = torch.nn.functional.normalize(q, dim=-1)
        k = torch.nn.functional.normalize(k, dim=-1)

        attn = (q @ k.transpose(-2, -1)) * self.temperature
        attn = attn.softmax(dim=-1)

        out = (attn @ v)
        
        out = rearrange(out, 'b head c (h w) -> b (head c) h w', head=self.num_heads, h=h, w=w)

        out = self.project_out(out)
        return out

qkv是1x1卷积，输出维度是输入三倍，qkv_dwconv是分组卷积，输出维度不变，chunk等分3个分别为q、k、v，即shape与输入x相同。

分别对q、k、v进行rearrage，多头设置进行通道数划分，q、k乘积前进行归一化，注意q、v shape为b head c h*w，v转置，则attn为b head c c，为文中所谓的通道间注意力。

GDFN

##########################################################################
## Gated-Dconv Feed-Forward Network (GDFN)
class FeedForward(nn.Module):
    def __init__(self, dim, ffn_expansion_factor, bias):
        super(FeedForward, self).__init__()

        hidden_features = int(dim*ffn_expansion_factor)

        self.project_in = nn.Conv2d(dim, hidden_features*2, kernel_size=1, bias=bias)

        self.dwconv = nn.Conv2d(hidden_features*2, hidden_features*2, kernel_size=3, stride=1, padding=1, groups=hidden_features*2, bias=bias)

        self.project_out = nn.Conv2d(hidden_features, dim, kernel_size=1, bias=bias)

    def forward(self, x):
        x = self.project_in(x)
        x1, x2 = self.dwconv(x).chunk(2, dim=1)
        x = F.gelu(x1) * x2
        x = self.project_out(x)
        return x

先是1x1，用于提取特征，注意参数ffn_expansion_factor，然后接一个3x3的dwconv，通道维度不变，按照维度划分两个x1、x2，其中一个进行gelu，project_out将维度恢复到x一样。

LayerNorm

## Layer Norm

def to_3d(x):
    return rearrange(x, 'b c h w -> b (h w) c')

def to_4d(x,h,w):
    return rearrange(x, 'b (h w) c -> b c h w',h=h,w=w)

class BiasFree_LayerNorm(nn.Module):
    def __init__(self, normalized_shape):
        super(BiasFree_LayerNorm, self).__init__()
        if isinstance(normalized_shape, numbers.Integral):
            normalized_shape = (normalized_shape,)
        normalized_shape = torch.Size(normalized_shape)

        assert len(normalized_shape) == 1

        self.weight = nn.Parameter(torch.ones(normalized_shape))
        self.normalized_shape = normalized_shape

    def forward(self, x):
        sigma = x.var(-1, keepdim=True, unbiased=False)
        return x / torch.sqrt(sigma+1e-5) * self.weight

class WithBias_LayerNorm(nn.Module):
    def __init__(self, normalized_shape):
        super(WithBias_LayerNorm, self).__init__()
        if isinstance(normalized_shape, numbers.Integral):
            normalized_shape = (normalized_shape,)
        normalized_shape = torch.Size(normalized_shape)

        assert len(normalized_shape) == 1

        self.weight = nn.Parameter(torch.ones(normalized_shape))
        self.bias = nn.Parameter(torch.zeros(normalized_shape))
        self.normalized_shape = normalized_shape

    def forward(self, x):
        mu = x.mean(-1, keepdim=True)
        sigma = x.var(-1, keepdim=True, unbiased=False)
        return (x - mu) / torch.sqrt(sigma+1e-5) * self.weight + self.bias


class LayerNorm(nn.Module):
    def __init__(self, dim, LayerNorm_type):
        super(LayerNorm, self).__init__()
        if LayerNorm_type =='BiasFree':
            self.body = BiasFree_LayerNorm(dim)
        else:
            self.body = WithBias_LayerNorm(dim)

    def forward(self, x):
        h, w = x.shape[-2:]
        return to_4d(self.body(to_3d(x)), h, w)

先将输入进行重排，b c h w转为b h*w c，对c维度进行求均值和方差，然后进行归一化，最后再重排到4维b c h w