1.中序遍历和后序遍历构建二叉树；

 TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) 
    {
        //判空
        if(postorder.size()== 0) return nullptr;

        //找到后序的最后元素就是根节点以及栈来存放数据
        auto root=new TreeNode(postorder[postorder.size()-1]);
        auto s=stack<TreeNode*>();

        //入栈
        s.push(root);
        //前序最后元素比较
        int inorderIndex=inorder.size()-1;
        //从最后第二个元素开始比较
        for(int i=int(postorder.size())-2;i>=0;i--)
        {
            //倒数第二个元素开始，排序node结点。
              int postorderVal=postorder[i];
              auto node=s.top();

             //如果不等于就是插入到右节点；
              if(node->val != inorder[inorderIndex])
              {
                  node->right=new TreeNode(postorderVal);
                  s.push(node->right);
              }
              //相等，将栈中元素作为左结点。
              else
              {
                  while(!s.empty() && s.top()->val==inorder[inorderIndex])
                  {
                    node=s.top();
                    s.pop();
                    inorderIndex--;
                  }
                  node->left=new TreeNode(postorderVal);
                  s.push(node->left);
              }
        }
        //多画图总结分析。
        return root;
    }

1.前序遍历和中序遍历构建二叉树；

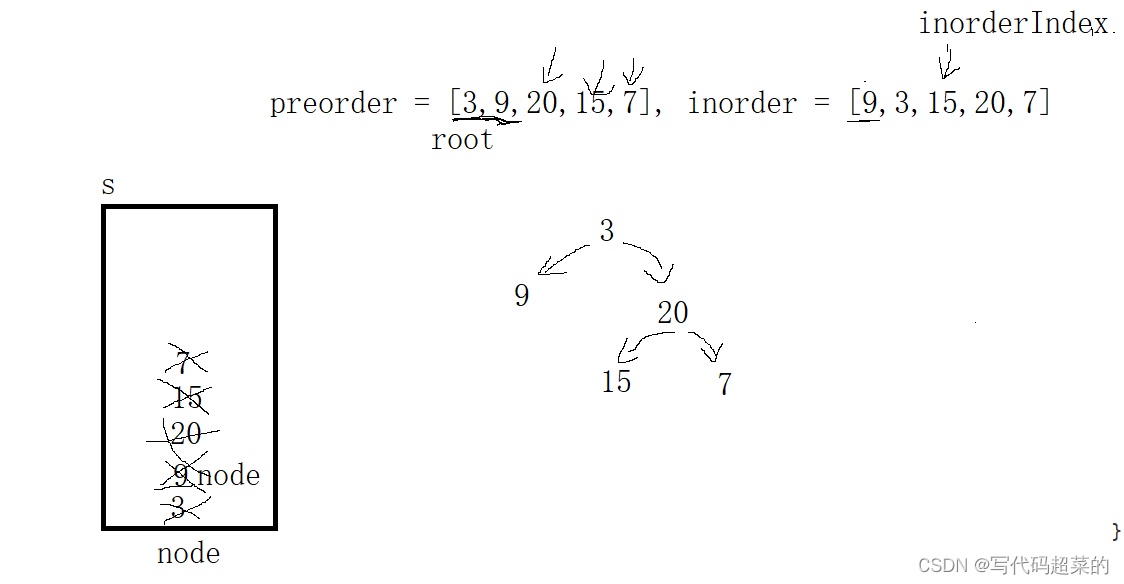
 TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) 
    {
        if(preorder.size()==0) return nullptr;

        TreeNode* root= new TreeNode(preorder[0]);
        stack<TreeNode*> stk;
        stk.push(root);
        int inorderIndex=0;
        
        for(int i=1;i<preorder.size();i++)
        {
            int preorderVal=preorder[i];
            TreeNode* node=stk.top();
            if(node->val != inorder[inorderIndex])
            {
                node->left=new TreeNode(preorderVal);
                stk.push(node->left);
            }
            else
            {
                while(!stk.empty() && stk.top()->val ==inorder[inorderIndex])
                {
                    node=stk.top();
                    stk.pop();
                    inorderIndex++;
                }
                node->right=new TreeNode(preorderVal);
                stk.push(node->right);
            }

        }
        return root;
    }

3.根据二叉树创建字符串；

 string tree2str(TreeNode* root) 
    {
       //为空直接返回；
       if(root == nullptr)
          return "";

       //左右都为空；返回root的值
       if(root->left == nullptr && root-> right == nullptr)
       {
           return to_string(root->val);
       }

       //左不为空，右边为空；root的值以及左节点的内容
       if(root->right == nullptr)
       {
           return to_string(root->val) + "(" + tree2str(root->left) + ")";
       }

       //最后就是左边为空，右边不为空的情况；左边也要加上()；右边也要访问。
       return to_string(root->val) + "(" + tree2str(root->left) + ")(" + tree2str(root->right)+")";
    }

4.二叉搜索树与双向链表；

TreeNode* head=nullptr;
	TreeNode* pre=nullptr;

    TreeNode* Convert(TreeNode* pRootOfTree) 
	{
        if(pRootOfTree ==nullptr) return nullptr;

		Convert(pRootOfTree->left);

		if(pre == nullptr)
		{
			pre=pRootOfTree;
			head=pRootOfTree;
		}
		else
		{
			pre->right=pRootOfTree;
			pRootOfTree->left=pre;
			pre=pRootOfTree;
		}
		Convert(pRootOfTree->right);
		return head;
    }

5.二叉树的公共祖先：

 TreeNode* ans=nullptr;
    
    bool dfs(TreeNode* root,TreeNode* p,
  TreeNode* q)
  {
      //判空
      if(root == nullptr) return false;
      
      //左右子树看一下
      bool lson =dfs(root->left,p,q);
      bool rson =dfs(root->right,p,q);
      
      //标记ans返回结点
      if((lson && rson) || (root->val ==p->val || root->val == q->val) && (lson || rson))
      {
          ans=root;
      }
      
      //递归返回()
      return rson || lson || root->val ==p->val || root->val == q->val;
  }
    
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) 
    {
        dfs(root,p,q);
        return ans;
    }

6.二叉树的层序遍历：

vector<vector<int>> levelOrder(TreeNode* root) 
    {
       vector<vector<int>> ret;
       if(root == nullptr) return ret;

       queue<TreeNode*> q;
       q.push(root);
       while(!q.empty())
       {
          int currentLevelSize = q.size();
          ret.push_back(vector<int>());
          
          for(int i=1;i <= currentLevelSize;i++)
          {
             auto node=q.front();
             q.pop();
             ret.back().push_back(node->val);
             if(node->left) q.push(node->left);
             if(node->right) q.push(node->right);
          }
       }
       return ret;
    }