1.第二类斯特林数：

2^n-1就是n个1的二进制，因为每一个&为0，所以我们可以把问题等价于n个1（不同的球）的串分配给m个非空的盒子，求方案数，这就转化成了第二类斯特林数。

我们令s(n,m)表示n个不同的球分配给m个相同非空的盒子。我们考虑s(n+1,m)，如果n个元素构成了m-1，那么第n+1个单独构成一个集合。如果n个元素构成了m，那么第n+1个随便放。

因此，s(n+1,m)=s(n,m-1)+m*s(n,m).

如何求通项公分式？

我们考虑带标号的盒子：

令Xi表示第i个子集为空(其他不知道）的方案数：

下面就是求第二类斯特林数的模板题，下面是AC代码（当模板）：

#include<bits/stdc++.h>
#define endl '\n'
#define int signed long long
#define double long double
using namespace std;
int N=2e5+10;
int mod=1e9+7;
vector<int> nxt(N);
int qpow(int n,int x)//快速幂
{
    int num=1;
    while(x)
    {
        if(x&1)
        {
            num=num*n%mod;
        }
        n=n*n%mod;
        x>>=1;
    }
    return num;
}
void solve()
{
    int n,m;
    cin >> n >> m;
    if(m>n)
    {
        cout << 0 << endl;
        return;
    }
    int ans=0;
    nxt[0]=1;
    for(int i=1;i<=m;i++) nxt[i]=nxt[i-1]*i%mod;//求阶乘
    for(int i=0;i<=m;i++)
    {
    ans=(ans+qpow(-1,m-i)*qpow(i,n)%mod*qpow(nxt[i],mod-2)%mod*qpow(nxt[m-i],mod-2)%mod+mod)%mod;//m的阶乘抵消了
    }
    cout << ans << endl;
}
signed main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    solve();
    return 0;
}

2.枚举：

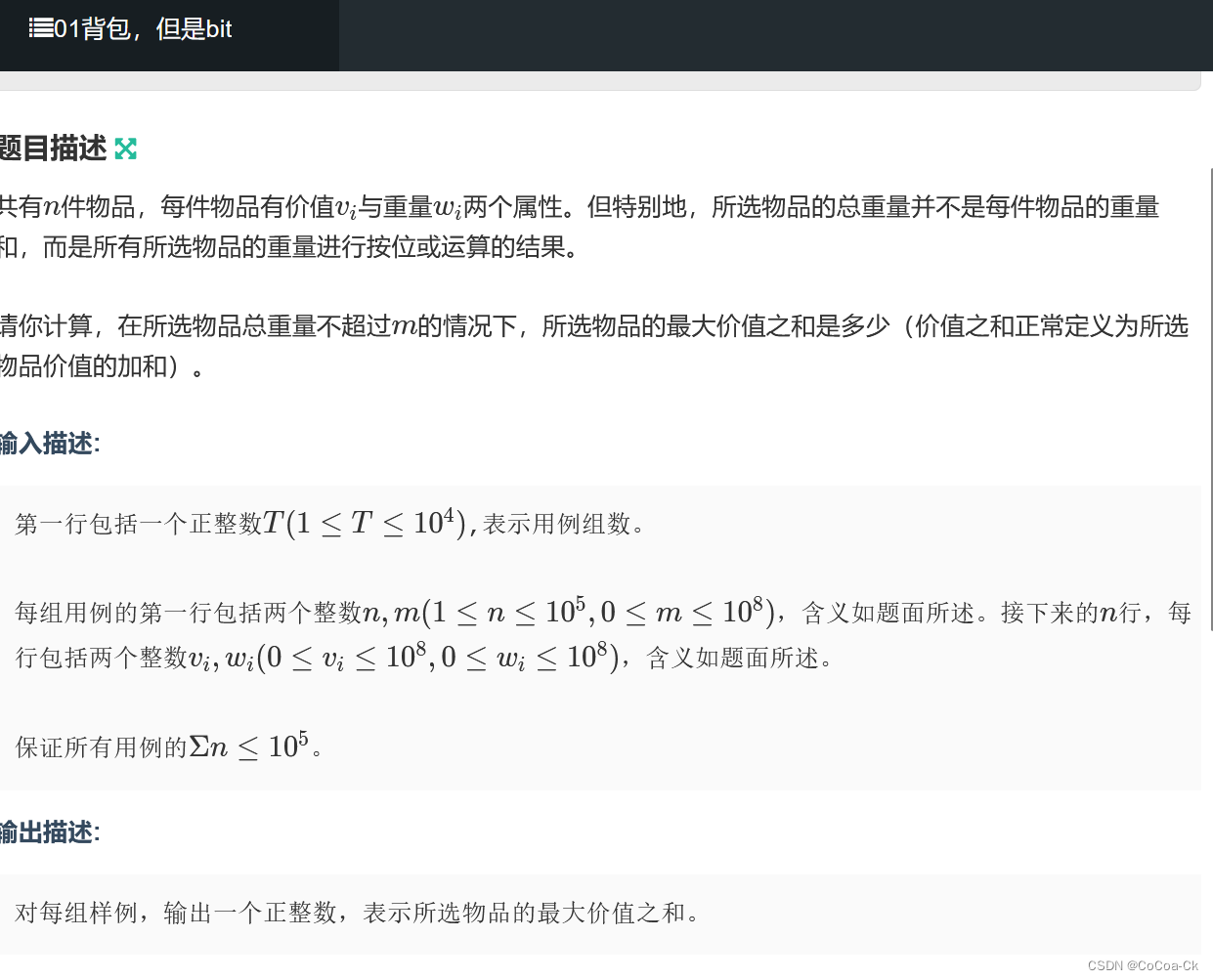
我们不妨对m的每一位二进制分析一下，假如第x位为1，那么我们选的时候在x为0，x的高位上要是它的子集，而其低位可以随便选，这样的w就是可以的并且不会产生影响，于是我们枚举x即可。

注意，我们需要对自己特判一下，下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
long long t,n,m,v[100010],w[100010];
long long ans;
void calc(long long x){
    long long res=0;
    for(int i=1;i<=n;i++){
        if((x&w[i])==w[i]) res+=v[i];
    }
    ans=max(res,ans);
}
void solve(){
    cin>>n>>m;
    ans=0;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    for(int i=30;i>=0;i--){
        if((m>>i)&1){
           calc(((1<<i)-1)|(m^(1<<i)));
        }
    }
    calc(m);
    cout<<ans;
}
int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    cin>>t;
    while(t--){
        solve();
        cout<<endl;
    }
}

3.基环内向树+搜索：

对于每一个ai,可以看成从连到ai,当i确定了，那么ai自然也确定了，同时，我们发现一共n条边，每一个点的出度一定为1，于是就形成了多个有一个环+几个分支形状的联通块，对于分支我们不用考虑，因为当环确定了分支自然也定了，而我们以一点为起点从A---E枚举，看看这个环的逻辑关系是否成立，然后把每一个联通块的数量相乘即可，下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,x,cnt;
int mod = 998244353;
string s[100010];
int vis[100010];
int edge[100010];
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++) cin>>edge[i]>>s[i];
    long long ans=1;
    for(int i=1;i<=n;i++){
       int j=i;
        while(vis[j]==0){
            vis[j]=i;
            j=edge[j];
        }
        if(vis[j]==i){
            long long sum=0;
            int k=j;
            int len=0;
             do{
                len++;
                k=edge[k];
            }while(k!=j);
            for(int x=0;x<5;x++){
                int v=x;
                for(int y=0;y<len;y++){
                    v=s[k][v]-'A';
                    k=edge[k];
                }
                sum+=(v==x);
            }
            ans=ans*sum%mod;
        }
    }
    cout<<ans;
}

在实现过程中，我们遍历一个联通块时可能不包含一个分支，而当我们走到它时，因为vis[j]!=i，于是就巧妙地消除了他的影响，同时，因为都一一确定，我们可以先把数求出来，然后再遍历，这样写比较直观简单。

4.暴力枚举：

注意到m的范围，我们可以知道绝对值>=2的最多30个，我们可以直接枚举，看上去n^2，但实际上因为check有很大部分远小于n,导致也可以过。

当n>30时，一定有-1/1，我们去枚举那个是1/-1.

当n<30时，不存在两个数都>1000，我们直接枚举即可

#include<bits/stdc++.h>
using namespace std;
int q,n,m,a[100010];
bool cmp(int a,int b){
    return a<b;
}
set<int> s={0};
bool check(int x){
     long long res = 1;
    for(int i = 1; i<=n; ++i){
        res *= a[i] + x;
        if(abs(res) >1000000000) return 0;
    }
    s.insert(res);
    return 1;
}
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    cin>>n>>q;
    for(int i=1;i<=n;i++) cin>>a[i];
    sort(a+1,a+n+1,cmp);
    if(n>30){
        for(int i=1;i<=n;i++){
        if(a[i]==a[i-1]) continue;
        check(-a[i]-1);
        check(-a[i]+1);
    }
    }
    else{
        for(int i=1;i<=n;i++){
        if(a[i]==a[i-1]) continue;
        for(int l = - a[i] - 1; check(l);l-- );
        for(int r = - a[i] + 1; check(r);r++ );
    }
    }

    for(int i=1;i<=q;i++){
        cin>>m;
        cout << (s.count(m)?"Yes":"No") <<'\n';
    }
}

5.二分+贪心

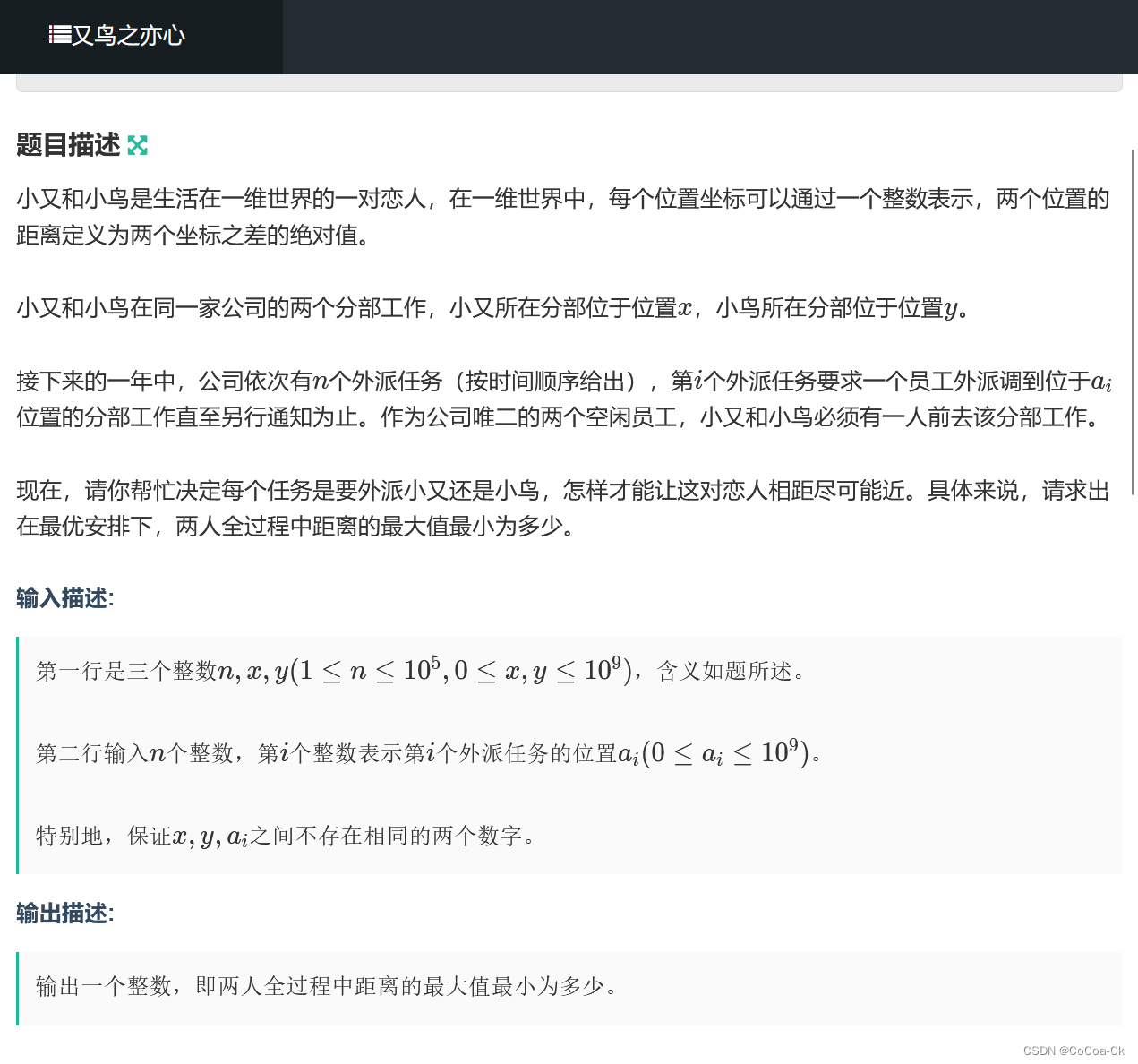
我们先二分一个值然后check.

那么我们如何check呢？

假如一个点在an,我们从后往前找第一个j使j+1--n的点到他的距离<=d,我们在从它向前找即可。如果可以到1就可以，到0的话就不行。

下面是贪心的正确性证明（参考某大佬）：

我们令mx记录j+1--i的位置max的点,mi为j+1--imin的点，如果当一个人确定后，另一个人的最后一个在j+1后，那么一定有个位置不符合，而如果我们从后往前找第一个j并选时，此时的范围从[mx-d,mi+d]变成了[aj-d,aj+d]，范围扩大了，此时前面可以选的范围就更大了，因此，我们可以保证正确的步骤一定可以被选到（若不选的话前面原本要选的可能因为范围限制而不能选）

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,x,y;
int a[100010];
bool check(int d){
    int tn=n;
    while(tn>1){
        int mx=a[tn],mi=a[tn];
        for(int i=tn-1;i>=0;i--){
            if(i==0) return 0;
            if(abs(a[i]-mx)<=d&&abs(a[i]-mi)<=d){
                tn=i;
                break;
            }
            mx=max(mx,a[i]);
            mi=min(mi,a[i]);
        }
    }
    return 1;
}
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    cin>>n>>x>>y;
    a[1]=x;
    a[2]=y;
    n+=2;
    for(int i=3;i<=n;i++) cin>>a[i];
    int l=abs(x-y),r=1e9;
    while(l<r){
        int mid=(l+r)/2;
        if(check(mid)) r=mid;
        else l=mid+1;
    }
    cout<<l;
}