---

题目

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例 1：

输入：n = 4
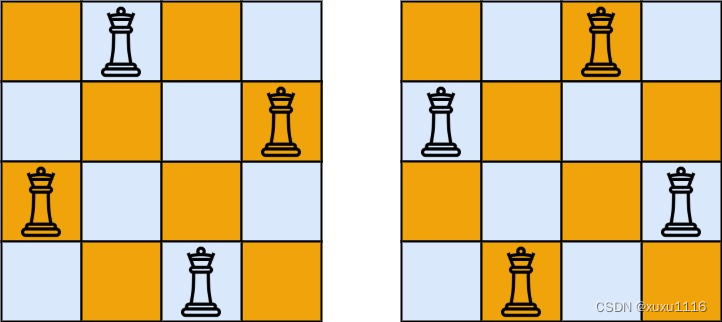
输出：[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[[“Q”]]

提示：

• 1 <= n <= 9

---

答案

我们定义三个数组 col, dg 和 udg，分别表示列、正对角线和反对角线上的是否有皇后，如果位置 (i,j) 有皇后，那么 col[j], dg[i+j] 和 udg[n−i+j] 都为 1。另外，我们用一个数组 g 记录当前棋盘的状态，初始时 g 中的所有元素都是 ‘.’。

接下来，我们定义一个函数 dfs(i)，表示从第 i 行开始放置皇后。

在 dfs(i) 中，如果 i=n，说明我们已经完成了所有皇后的放置，我们将当前 g 放入答案数组中，递归结束。

否则，我们枚举当前行的每一列 j，如果位置 (i,j) 没有皇后，即 col[j], dg[i+j] 和 udg[n−i+j] 都为 0，那么我们可以放置皇后，即把 g[i][j] 改为 ‘Q’，并将 col[j], dg[i+j] 和 udg[n−i+j] 都置为 1，然后继续搜索下一行，即调用 dfs(i+1)，递归结束后，我们需要将 g[i][j] 改回 ‘.’ 并将 col[j], dg[i+j] 和 udg[n−i+j] 都置为 0。

在主函数中，我们调用 dfs(0) 开始递归，最后返回答案数组即可。

时间复杂度 (n² ×n!)，空间复杂度 O(n)。其中 n 是题目给定的整数。

class Solution(object):
    def solveNQueens(self, n):
        """
        :type n: int
        :rtype: List[List[str]]
        """
        def dfs(i):
            if i == n:
                ans.append(["".join(row) for row in g])
                return
            for j in range(n):
                if col[j] + dg[i + j] + udg[n - i + j] == 0:
                    g[i][j] = "Q"
                    col[j] = dg[i + j] = udg[n - i + j] = 1
                    dfs(i + 1)
                    col[j] = dg[i + j] = udg[n - i + j] = 0
                    g[i][j] = "."

        ans = []
        g = [["."] * n for _ in range(n)]
        col = [0] * n
        dg = [0] * (n << 1)
        udg = [0] * (n << 1)
        dfs(0)
        return ans

---

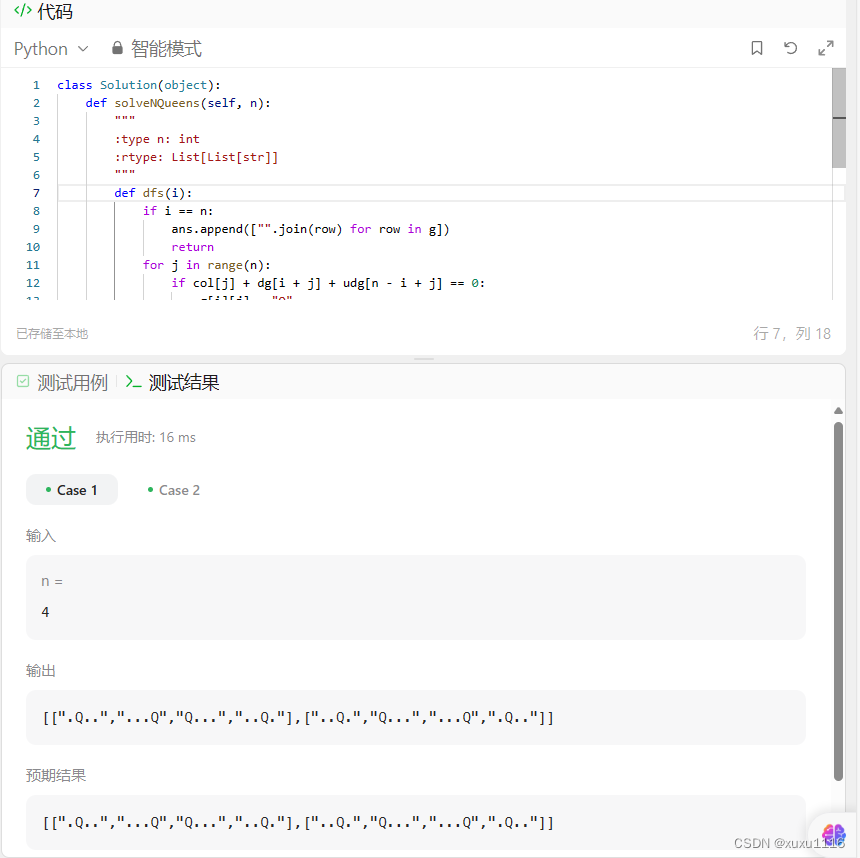
运行结果