一、概述
由于最近写论文需要使用复杂网络知识中的半局部中心法,但是截止目前来说,网上几乎搜索不到有关的MATLAB程序代码,只有一篇用Python编写的程序,我的电脑中没有python,所以我花费一些时间,利用matlab进行编写,结果显示和Python编写的博主一样。下面我分享一下我的编程思路,希望大家能够独立思考,不要对代码进行直接复制,只放置局部代码,如有需要请订阅后留言,最终结果如下所示。
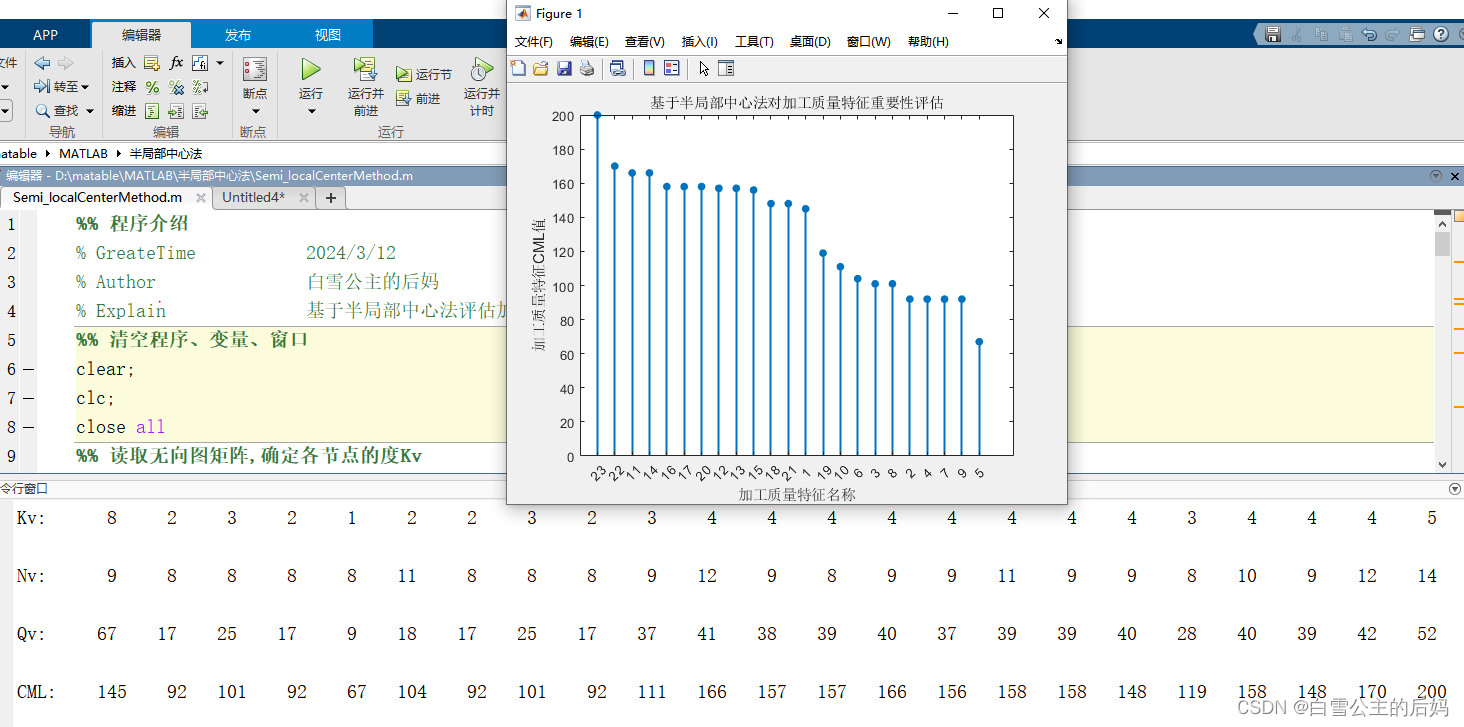
matlab编写的结果

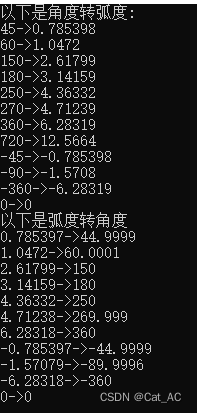
Python博主编写的
我们可以直观的看到两者结果一致
二、半局部中心法介绍
复杂网络的影响力度量中,最常用的度中心性的度量只是局限于节点自身,对于节点的邻域和所在网络的拓扑结构都没有考虑,因此局限性很大。度中心性,认为节点连接的邻居越多,则它在影响力传播中的地位越重要。这种度量影响力,的方法缺陷在于,节点影响力会被它的邻域内节点的影响力所影响,还会被自身,所处的网络位置所影响,而度中心性无法考虑到这些因素。因此有人提出了半局,部中心性,半局部中心性认为节点的影响力不仅跟自身度值有关,还跟它邻域内的节点影响力有关。
大部分基于局部网络结构的度量的缺点都是没有充分考虑网络拓扑结构对节点重要性的影响,导致总体上计算结果准确度不高。因此Chen等人提出了半局部中心性(Semi-Local Centrality,LC)度量,将局部信息的计算范围扩大到次近邻的范围。该方法是对局部信息计算和对全局信息计算方法的折中,但本质上仍然是基于局部结构的方法。首先定义N(w)为节点Vw的两层邻居度,其值等于从 Vw出发 2步内可到达的邻居的数目, 然后定义

三、实现思路
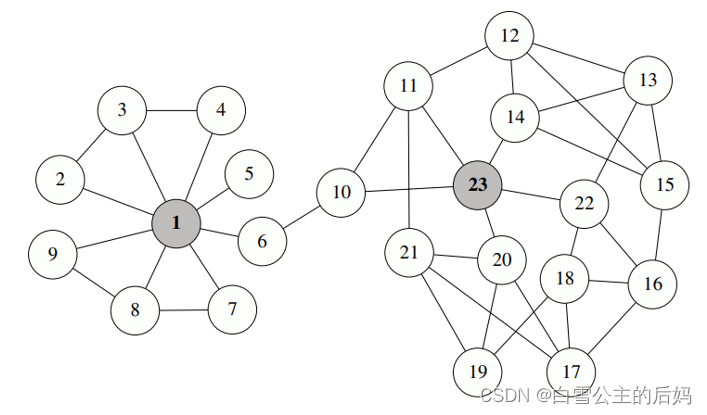
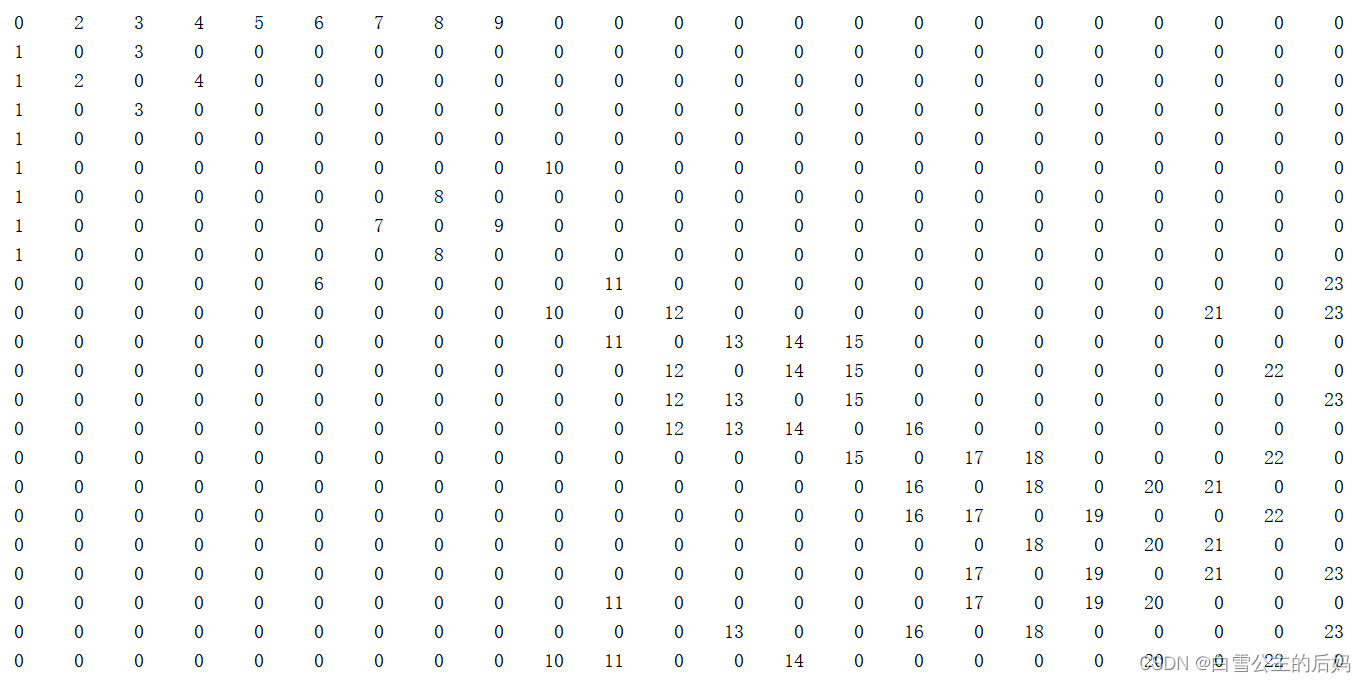
1、导入用Excle编写好的邻接矩阵,两个节点有关联用1,无关联用0,效果如下所示

2、查找邻接矩阵中的具体节点名字
3、确定各节点的度Kv,即矩阵中每行不为0的个数

4、确定各节点两步之内可以到达的邻居数目Nv,分别求取节点i的一步相邻节点,然后在加上相邻节点的相邻节点,然后去掉重复的节点即可,去重是关键这里用到matlab自己的函数unique( )
![]()
5.确定各节点两步之内可以到达的邻居数目Qv,对各节点的相邻节点的Nv求和。
![]() 6、确定各节点四阶邻居数目CML,对节点的i的相邻节点的Qv求和。
6、确定各节点四阶邻居数目CML,对节点的i的相邻节点的Qv求和。
![]()
综上所述就可以实现半局部中心法求取SLC(i).
四、代码如下
%% 程序介绍
% GreateTime 2024/3/12
% Author 白雪公主的后妈
% Explain 基于半局部中心法评估加工质量特征的重要性
%% 清空程序、变量、窗口
clear;
clc;
close all
%% 读取无向图矩阵,确定各节点的度Kv
Date = xlsread('C:\Users\NINGMEI\Desktop\Date1.xlsx','sheet6');
for i=1:size(Date,1)%矩阵Date的行数
for j=1:size(Date,2)
if Date(i,j)>0
Node(i,j)=j;
end
end
end
Kv=sum(Node~=0,2);
%% 读取无向图矩阵,确定各节点相邻节点的度Nv
for h=1:size(Node,1)
number=1;
Node1=zeros(size(Node,1),size(Node,2));
for k=1:size(Node,2)
。。。。。。
end
。。。。。。
end
%% 确定各节点两步之内可以到达的邻居数目Qv
。。。。。
。。。。。。
。。。。。。
%% 确定各节点四阶邻居数目CML
。。。。。
。。。。。
。。。。。
%% 命令行窗口输出
fprintf('Kv: ');
disp(Kv');
fprintf('Nv: ');
disp(Nv');
fprintf('Qv: ');
disp(Qv);
fprintf('CML: ');
disp(CML);
%% 绘图
[Weight, Sort]=sort(CML,'descend');% 按CML降序排序
x =1:size(Sort,2);
y=Weight;
hh=stem(x,y,'Marker','none');
hh.LineWidth=1.5;
xlim([0 size(Sort,2)+2])
hold on;
plot(x,y,'.','Color',[0 0.45 0.74],'MarkerSize',20);
Name=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23];
for h=1:size(Name,2)
Name1(1,h)=Name(1,Sort(:,h));
end
set(gca,'XTickLabel',Name1);
xticks(1:1:size(Sort,2)); %这样x轴会每隔10显示一个刻度
xtickangle(45);
%在图表中添加标题和轴标签
title('基于半局部中心法对加工质量特征重要性评估')
xlabel('加工质量特征名称')
ylabel('加工质量特征CML值')