算法－图的存储，图的转置，拓扑排序

news2024/12/24 21:17:14

1.图的存储
图用来对关系建模．图是节点和边构成的集合．节点反映图的元素集合，边反映图的元素集合中元素间的关系．
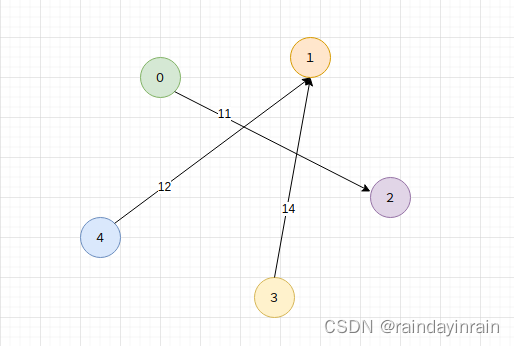
在这里插入图片描述
上述是由五个节点，三条边构成的结构．我们可以用图对其建模．

对由节点，边构成的集合采用图结构表示时候，我们可以有两种基本选择，这两种基本选择引出图结构两种基本存储方式：邻接表存储，矩阵存储．

(1). 邻接表存储
我们依次存储图中每个节点，对节点间关系采用邻接表方式．
针对上述实例，具体为：

#include <stdio.h>
#include <stdlib.h>
template<class EdgeInfo>
class AdjNode{
public:
    AdjNode* m_pNext = nullptr;
    EdgeInfo m_stInfo;
    int m_nId;
};
template<class T, class EdgeInfo>
class Node{
public:
    T m_stEle;
    AdjNode<EdgeInfo>* m_pList = nullptr;
};
int main(){
    Node<int, int> stNodes[5];
    AdjNode<int> stAdjNode[3];
    stAdjNode[0].m_nId = 2;
    stAdjNode[0].m_stInfo = 11;
    stAdjNode[1].m_nId = 1;
    stAdjNode[1].m_stInfo = 14;
    stAdjNode[2].m_nId = 1;
    stAdjNode[2].m_stInfo = 12;
    stNodes[0].m_pList = &stAdjNode[0];
    stNodes[3].m_pList = &stAdjNode[1];
    stNodes[4].m_pList = &stAdjNode[2];
}

这种表示方法下，通过节点可以找到以该节点为起点的所有边的信息．
(2). 矩阵存储
我们依次存储图中每个节点，对节点间关系采用矩阵方式存储．
针对上述实例，具体为：

#include <stdio.h>
#include <stdlib.h>
template<class T>
class Node{
public:
    T m_nEle;
};
template<class EdgeInfo>
class Edge{
public:
    bool m_bValid = false;
    EdgeInfo m_stInfo;
};
int main(){
    Node<int> stNodes[5];
    Edge<int> stEdges[5][5];
    stEdges[0][2].m_bValid = true;
    stEdges[0][2].m_stInfo = 11;
    stEdges[4][1].m_bValid = true;
    stEdges[4][1].m_stInfo = 12;
    stEdges[3][1].m_bValid = true;
    stEdges[3][1].m_stInfo = 14;
}

这种表示方法下，通过矩阵来存储所有边的信息．

(3). 总结
当图的边的数量较少时，采用邻接表方式，比较节省空间．
当图的边的数量较多时，采用矩阵方式，有助于快速定位边的信息和存在性．

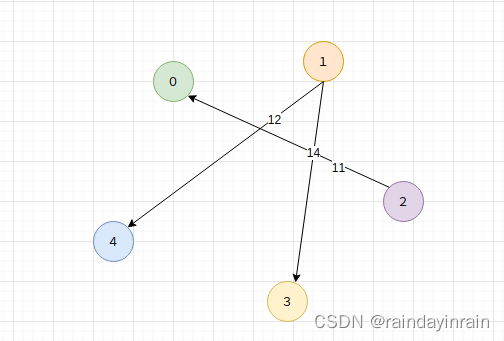
2.图的转置
即逆转图中的关系．
针对上述实例，转置处理后示意图如下：
在这里插入图片描述
3.拓扑排序
(1). 定义
拓扑排序是对一个有向无环图的顶点进行排序的过程。这个排序的目的是将图中的所有顶点排成一个线性序列，使得对于图中的任意一对顶点u和v，如果存在一条从u到v的边，那么u在线性序列中的位置就出现在v之前。这样的线性序列被称为满足拓扑次序的序列，简称拓扑序列。

拓扑排序在计算机科学和图论中具有重要的应用。它常被用来确定一个依赖关系集中，事物发生的顺序。例如，在一个工程项目中，各个子工程（或任务）之间可能存在一定的依赖关系，即一个子工程必须在另一个子工程完成后才能开始。通过拓扑排序，我们可以得到一个合理的子工程执行顺序，从而确保项目能够顺利进行。
(2). 实例
拓扑排序的一个实例可以是一个课程安排的场景。假设我们有一个学校的课程安排，其中一些课程是其他课程的前置课程，也就是说，在修读某些课程之前，必须先完成其他特定的课程。我们可以将这些课程看作有向无环图中的顶点，而将前置课程关系看作图中的有向边。

例如，假设我们有以下课程及其前置课程关系：
课程A是课程B的前置课程．
课程B是课程C和课程D的前置课程．
课程C是课程E的前置课程．
这可以表示为以下的有向无环图：
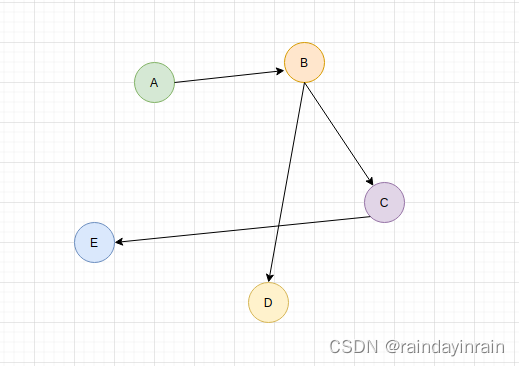
在这里插入图片描述
现在，我们想要对这些课程进行拓扑排序，以确定一个学生可以按照该顺序完成所有课程的合理学习路径。使用拓扑排序算法，我们可以得到以下的一个可能的拓扑序列：A -> B -> C -> D -> E．
(3). 算法实现
a. 创建一个队列，并将所有入度为0的顶点加入队列，一个存储拓扑排序结果的集合。
b. 当队列非空时，循环执行以下步骤：
b.1. 从队列中取出一个顶点。
b.2. 将其添加到结果集合尾部。
c.2. 对于该顶点的所有邻接顶点，将其入度减1。如果入度变为0，则将该邻接顶点加入队列。
c. 如果图中还有顶点未被输出，则图中存在环，无法进行拓扑排序．否则，算法结束．