导 读

我最近从事一个项目，需要在 matplotlib 中进行一些微调的子图和叠加。虽然我对制作基本的可视化感到很舒服，但我很快发现我对子图系统的理解没有达到标准。于是回到基础知识，并花了一些时间阅读文档并在 Stack Overflow 上搜索相关示例和解释。

当我开始了解 mateplotlib 的子图系统如何工作时，我意识到，如果有UI 工具，可以在其中测试代码并准确查看图中的样子学习起来会容易得多。

于是Github找到了相关的工具。

地址：

Matplotlib Plot Plannerhttps://qed0711.github.io/plot-planner/

有需要的朋友关注公众号【小Z的科研日常】，获取更多内容。

01.add_subplot()

figure.add_subplot() 方法是将现有图形对象划分为不同大小的不同区域的最简单方法之一。

它返回一个轴对象，并接受三个整数。如果这些整数中的每一个都是单个数字，则它们可以简化为单个三位数整数。

例如，.add_subplot(1, 2, 3) 可以简化为 .add_subplot(123)。但这些数字到底意味着什么？

关键是要理解前两个整数定义了图形的划分，最后一个数字实际上说明了子图应该在该划分中的位置。因此，如果将子图定义为 (2,3,1)，则意味着将子图分解为 2 x 3 网格，并将新子图放置在该网格的第一个单元格中。

我们工具中尝试一下。将使用 5 个不同大小的子图来制作如下所示的示例。

我们将从标记为ax1（红色）的开始。只要看一下图像，就会发现 ax1 占据了图形区域的左半部分。首先，我们将定义图形并将其设为 8x8 正方形（图形大小是任意的，但对于本例来说效果很好）。然后，忽略所有其他子图，让我们将图形分成左右两部分。

fig = plt.figure(figsize=(8,8))
fig.add_subplot(1, 2, 1)

在这种情况下，这些数字的意思是——将我的图形划分为 1 行和 2 列。最后一个数字表示要使用哪个单元格。

这里奇怪的是，子图的索引从 1 开始，而不是您想象的那样从 0 开始。因此，当我们说使用子图 1 时，我们是在告诉图形进入第一个子图的空间。

这是一个非常简单的情节，但更复杂的情节可能会变得难以记住。这是因为每个子图都是独立的，并且我们不会显示未选择的子图。但这里有一张来自情节规划应用程序的图像，可能会让整个事情变得更加明确。

我发现这个可视化比我看到的任何解释都清晰得多。我们可以看到 1 行和 2 列。然后，以绿色突出显示，我们可以看到索引号为 1 的单元格是我们选择的子图。

可能会认为，既然刚刚将图形分为左右两部分，那么现在唯一的其他选择就是将右半部分留空或在该子图中绘制一些内容。不是这种情况。

我们定义的每个新子图并不关心我们已经制作的任何其他子图。本质上，每个新的子图都会很高兴地准确地到达你告诉它去的地方，无论已经存在什么其他子图。

考虑到这一点，让我们创建ax2子图（蓝色）。再次查看该图像，ax2 似乎占据了该图的右上象限。再次强调，我们将忘记所有其他子图（甚至是我们已经制作的子图），我们将只专注于在右上角制作一个新的子图。

为此，我们要将图形空间分成 4 个象限并选择右上象限。让我们再看一下，看看它是如何工作的。

由此看来，我们想要一个 2x2 网格，并且想要第二个子图。绘图索引首先按行编号，然后按列编号。所以我们的代码是：

fig.add_subplot(2,2,2)

对于ax3（黄色），它看起来大约是 ax2 插槽垂直尺寸的一半，并且出现在它的正下方。基本上，我们正在寻找这个：

这将是 4 行 x 2 列，是第 6 个子图。或者：

fig.add_subplot(4,2,6)

最后两个子图看起来大小相同。在这里看到确切的比例有点困难，所以我只是表达，我们正在寻找 8 行 x 2 列的图形除法。它应该看起来像这样，我们想要为我们的两个新轴获取第 14 和 16 个子图。

fig.add_subplot(8,2,14)
fig.add_subplot(8,2,16)

现在我们的图形应该完全充满了子图。下面是完整的代码，其中添加了一些代码，以使其他一些视觉元素（颜色、标签等）正常工作。

import matplotlib.pyplot as plt
fig = plt.figure(figsize=(8,8))
ax1 = fig.add_subplot(1, 2, 1, xticklabels=[], yticklabels=[], xticks=[], yticks=[], fc="red",)
ax2 = fig.add_subplot(2, 2, 2, xticklabels=[], yticklabels=[], xticks=[], yticks=[], fc="blue")
ax3 = fig.add_subplot(4, 2, 6, xticklabels=[], yticklabels=[], xticks=[], yticks=[], fc="yellow")
ax4 = fig.add_subplot(8, 2, 14, xticklabels=[], yticklabels=[], xticks=[], yticks=[], fc="green")
ax5 = fig.add_subplot(8, 2, 16, xticklabels=[], yticklabels=[], xticks=[], yticks=[], fc="orange")
ax1.text(0.5, 0.5, "ax1", horizontalalignment='center', verticalalignment='center')
ax2.text(0.5, 0.5, "ax2", horizontalalignment='center', verticalalignment='center')
ax3.text(0.5, 0.5, "ax3", horizontalalignment='center', verticalalignment='center')
ax4.text(0.5, 0.5, "ax4", horizontalalignment='center', verticalalignment='center')
ax5.text(0.5, 0.5, "ax5", horizontalalignment='center', verticalalignment='center')
plt.show()

.add_subplot() 方法是一个强大的工具，但它有其局限性。例如，创建的每个子图只能占用一个单元格。

这意味着 .add_subplot() 不可能实现如下所示的操作（尽管它看起来更简单）

这里的问题是红色子图占据了图表左侧的 2/3。不幸的是，.add_subplot() 无法处理选择图形区域的 2/3。

为此，我们可以使用 .subplot2grid()。

02.subplot2grid

与 .add_subplot() 一样，.subplot2grid() 返回一个轴对象，其中包含有关新子图应放置在何处的信息。

它接受两个必需的位置参数：shape 和 loc。

shape 参数作为两个数字的列表或元组传入，其功能类似于 .add_subplot() 方法中的前两个数字。它们指定网格布局，第一个数字是行数，第二个数字是列数。

第二个参数 loc 代表位置，也是两个数字的列表或元组。与 .add_subplot() 不同，不需要通过在网格上指示单个索引来指定放置子图的位置。相反，可以通过指定要放置子图的行号和列号来选择网格索引。同样不同的是， .subplot2grid() 索引从 0 开始。因此 (0,0) 将是第一行和第一个单元格网格的列。

除了这两个参数之外，还有两个可选的关键字参数，rowspan和colspan。这就是我们真正发挥 .subplot2grid() 作用的地方。

一旦有了网格布局（形状）和起始索引（loc），就可以使用这两个参数扩展选择以占用更多行或列。默认情况下，rowspan 和 colspan 都设置为 1，这意味着 — 占用 1 行 1 列的单元格。当增加这些数字时，可以告诉轴对象占用当前网格布局中可用的尽可能多的相邻行和列。

让我们仔细看看上面的例子，其中只有 3 个子图。虽然其中一些子图可以（并且可能应该）使用 .add_subplot() 创建，但我们将在此处对所有子图使用 .subplot2grid() 进行练习。

正如我已经说过的红色子图，我们需要它占据总高度的 2/3。那么我们如何使用 .subplot2grid() 来做到这一点呢？除了占据行的三分之二之外，它还绘制在两列的左列中。有了这些信息，我们将网格拆分为 3 行 x 2 列，并将起始索引设置为左上角的单元格。

最后，我们需要告诉子图占据三行中的两行。我们通过将 rowspan 参数设置为 2 来实现这一点。因此，我们的网格和子图应该如下所示。

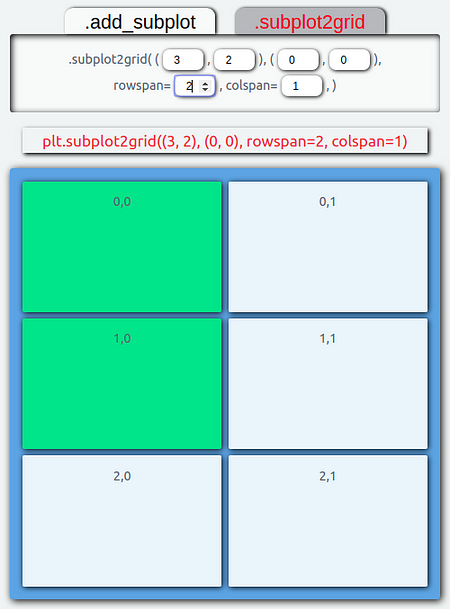
plt.subplot2grid((3, 2), (0, 0), rowspan=2, colspan=1)

.subplot2grid() 还需要一些更多的东西。但它可以非常精确地设置可视化的空间！

接下来我们将处理蓝色网格框。就像我说的，你可以使用 .add_subplot() （fig.add_subplot(325)）来做到这一点。但我们也可以使用 .subplot2grid() 来完成此任务。在我们的 3x2 网格中，我们希望该子图占据左下角的单元格。下面的绘图规划器的图像对此进行了描述。

我们的网格形状是相同的 (3,2)。由于我们只选择一个单元格，因此我们将 rowspan 和 colspan 设置为 1。我们只需要指出正确单元格的 loc 参数即可。方便的是，绘图规划器应用程序中的单元格标有该单元格在网格中的位置（尽管它们并不难找出）。从上图中，我们需要单元格 (2,0)，因此我们只需将其插入到我们的 loc 参数中即可。代码将是：

plt.subplot2grid((3, 2), (2, 0), rowspan=1, colspan=1)

对于最后一个子图，我们只需要整个右列。同样，这可以通过 .add_subplot(122) 轻松完成。

我们也可以使用 plt.subplot2grid((3, 2), (0, 1), rowspan=3, colspan=1) 来完成。

我们还可以使用以下代码来完成这个正确的列。这只是为了展示可以做什么，而不是如何解决此问题的实际建议。

plt.subplot2grid((6, 6), (0, 3), rowspan=6, colspan=3)

将所有这些放在一起，我们得到以下内容（我再次添加了一些额外的代码来处理颜色和文本）：

fig = plt.figure(figsize=(8,8))
ax1 = plt.subplot2grid((3, 2), (0, 0), rowspan=2, colspan=1, xticklabels=[], yticklabels=[], xticks=[], yticks=[], fc="red",)
ax2 = plt.subplot2grid((3, 2), (2, 0), rowspan=1, colspan=1, xticklabels=[], yticklabels=[], xticks=[], yticks=[], fc="blue",)
ax3 = plt.subplot2grid((3, 2), (0, 1), rowspan=3, colspan=1, xticklabels=[], yticklabels=[], xticks=[], yticks=[], fc="orange",)
ax1.text(0.5, 0.5, "ax1 \n(rows = 2/3)", horizontalalignment='center', verticalalignment='center')
ax2.text(0.5, 0.5, "ax2", horizontalalignment='center', verticalalignment='center')
ax3.text(0.5, 0.5, "ax3", horizontalalignment='center', verticalalignment='center')
plt.show()

再次得到视觉效果：