原题链接:64. 最小路径和
题目难度:中等
题目描述
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
**说明:**每次只能向下或者向右移动一步。
示例 1:

输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 2000 <= grid[i][j] <= 100
解题思路
这题是动态规划中比较简单的题型了,但是力扣给他的难度定位是中等哈哈哈,估计是个dp就算中等。
- 根据题目说明 每次只能向下或者向右移动一步,很明显是可以用dp(即动态规划)来做的,而且状态变化公式也非常明显,就差直接告诉你 “每个格子可以由上面或者左边的格子过来” 这句话了。
- 题目要求出从起点到终点路径数字总和最小的值,那很明显就是取上面和左边两个格子的最小值了,状态公式也很明显了:
dp[i][j] = dp[i][j] + Math.min(dp[i][j-1], dp[i-1][j]); - 需要注意的是边界处理,当
i == 0时或当j == 0时,是不用比较最小值的,因为只有一条路走,没得选择。还需要注意i和j都等于0的时候,这是起点,不需要加任何值。
完整解题代码 Java
class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
for (int i = 0 ; i < m; i++){
for (int j = 0 ; j < n ; j++){
if (i == 0 && j == 0) continue;
else if (j == 0) grid[i][j] += grid[i-1][j];
else if (i == 0) grid[i][j] += grid[i][j-1];
else grid[i][j] += Math.min(grid[i-1][j] , grid[i][j-1]);
}
}
return grid[m-1][n-1];
}
}
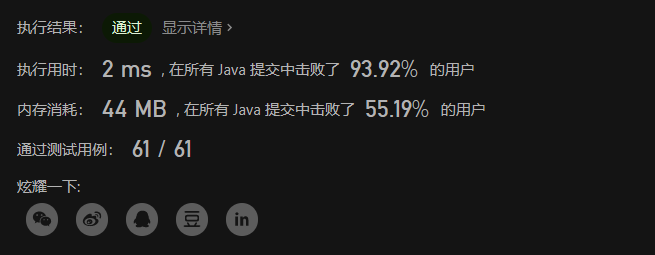
通过截图:
同类题型推荐
写LeetCode热题TOP100时我还遇到了几道跟这题很类似的题目,但是都比较简单,就不是太想写题解了。一并分享给大家,拿去练练手,掌握相似题型。
- 62. 不同路径 - 力扣(LeetCode) 难度:中等
- 70. 爬楼梯 - 力扣(LeetCode) 难度:简单






![[ 数据结构 ] 背包问题(动态规划)](https://img-blog.csdnimg.cn/img_convert/535b7a89319ab66170ef73a8a0894aef.png)