【模板】最小生成树（C++）

news2024/11/15 9:26:39

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出 orz。

输入格式

第一行包含两个整数 $N, M$ ，表示该图共有 $N$ 个结点和 $M$ 条无向边。

接下来 $M$ 行每行包含三个整数 $X_i,Y_i,Z_i$ ，表示有一条长度为 $Z_i$ 的无向边连接结点 $X_i,Y_i$ 。

输出格式

如果该图连通，则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。

样例 #1

样例输入 #1

样例输出 #1

提示

数据规模：

对于 $20\%$ 的数据， $N\le 5$ ， $M\le 20$ 。

对于 $40\%$ 的数据， $N\le 50$ ， $M\le 2500$ 。

对于 $70\%$ 的数据， $N\le 500$ ， $M\le 10^4$ 。

对于 $100\%$ 的数据： $1\le N\le 5000$ ， $1\le M\le 2\times 10^5$ ， $1\le Z_i \le 10^4$ 。

样例解释：

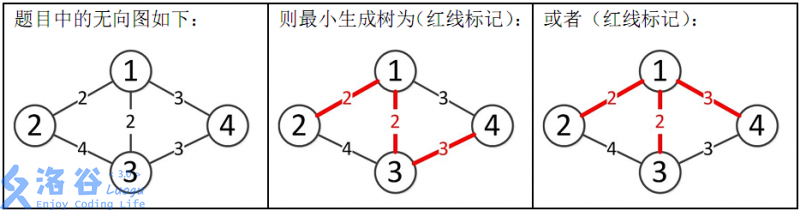
所以最小生成树的总边权为 $2 + 2 + 3 = 7$ 。

解题思路：

本题是最小生成树的模板题，这里介绍如何将一张图变成一棵最小生成树

最小生成树包含图中的所有节点，符合树的特性（无环、重边），同时要求这棵树的边权和最小

图可以变成一棵树的前提是图是连通的

接下来介绍prim算法

prim算法的本质是贪心

基本思想：首先任意选一个节点加入树中，

然后尝试由新加入的节点更新其他节点到树的最短距离

更新之后，加入距离树最近的节点，如此循环

思想很好理解吧，接下来介绍如何实现

首先要区分加入树和没有加入树的节点，这很容易实现，通过一个标记数组book即可

如何获取到树的最近节点是关键

获取方法一：

要知道到树的最近节点，就要知道每一个节点到树的最短距离

所以开一个数组dist维护最短距离

每加入一个新节点node，尝试用该新节点去更新最短距离数组dist

然后从更新后的数组选出距离树最近的节点temp加入，如此循环即可

bool prim() {
	int node = 1;
	dist[node] = 0;
	book[node] = true;//初始化
	
	for (int i = 2; i <= n; i++) {//循环加入n - 1个节点
		int temp = 0;
		int min_dist = NaN;//初始化
		
		for (int j = 1; j <= n; j++) {//尝试更新到树的最短距离
			if (!book[j]) {//未加入树
            	if (dist[j] > map[node][j]) {
					dist[j] = map[node][j];
				}
				if (min_dist > dist[j]) {
					min_dist = dist[j];
					temp = j;
				}
			}
		}
		
		if (temp) {//找到新节点
			book[temp] = true;
			node = temp;
		}
		else false;//图不连通，无法生成最小生成树
	}
	
	return true;//生成最小生成树
}

获取方法二：

采用优先队列 + 链式前向星实现，不了解的建议先去学习一下

思路基本一致，不再说明

这里特别说明几点：1）pair<int, int>(最短距离，节点)；2）保证队首节点距离树最近

void prim() {
	//初始化
	dist[1] = 0;
	p_q.push(pair<int, int>(0, 1));

	while (!p_q.empty()) {
		int node = p_q.top().second;
		p_q.pop();//取出首节点

		if (book[node]) continue;//已加入树
		book[node] = true;//未加入树

		for (int i = head[node]; i != -1; i = edges[i].next) {//尝试更新到树的最小距离
			int v = edges[i].v;
			if (!book[v] && dist[v] > edges[i].p) {//更新
				dist[v] = edges[i].p;
				p_q.push(pair<int, int>(dist[v], v));
			}
		}
	}
}

这里采用方法二解决本题

学会了如何生成最小生成树，本题就会迎刃而解

需要做的只是累计加入树的节点数量，判断是否生成成功

累计数的边权和，如果生成成功，输出

AC代码如下

//最小生成树
#include <iostream>
#include <vector>
#include <queue>
#include <memory.h>
using namespace std;
const int max_n = 5000;
const int max_m = 2e5;
const int max_z = 1e4;
const int NaN = 0x3F3F3F3F;

class greater_queue {
public:
	bool operator()(pair<int, int>p_1, pair<int, int>p_2) {
		return p_1.first > p_2.first;
	}
};

priority_queue<pair<int, int>, vector<pair<int, int>>, greater_queue>p_q;
struct edge { int v, p, next; }edges[max_m * 2];
int head[max_n + 1] = { -1 };
int tot = -1;
int dist[max_n + 1] = { NaN };
int book[max_n + 1] = { false };//最小生成树
int sum_dist = 0, sum_node = 0;

void add_edge(int u, int v, int p) {
	edges[++tot] = { v,p,head[u] }; head[u] = tot;
	edges[++tot] = { u,p,head[v] }; head[v] = tot;
}

void prim() {
	//初始化
	dist[1] = 0;
	p_q.push(pair<int, int>(0, 1));

	while (!p_q.empty()) {
		int node = p_q.top().second;
		p_q.pop();//取出首节点

		if (book[node]) continue;//已加入树
		book[node] = true;//未加入树
		sum_dist += dist[node];//累加边权
		sum_node--;//未加入的节点数量 - 1

		for (int i = head[node]; i != -1; i = edges[i].next) {//尝试更新到树的最小距离
			int v = edges[i].v;
			if (!book[v] && dist[v] > edges[i].p) {//更新
				dist[v] = edges[i].p;
				p_q.push(pair<int, int>(dist[v], v));
			}
		}
	}
}

int main() {
	memset(head + 1, -1, sizeof(int) * max_n);
	memset(dist + 1, 0x3F, sizeof(int) * max_n);
	int n, m, u, v, p;
	cin >> n >> m;
	sum_node = n;
	for (int i = 0; i < m; i++) {
		cin >> u >> v >> p;
		add_edge(u, v, p);
	}

	prim();

	if (sum_node) cout << "orz";
	else cout << sum_dist;
	return 0;
}