图论（蓝桥杯 C++ 题目 代码 注解）

news2024/11/25 22:44:54

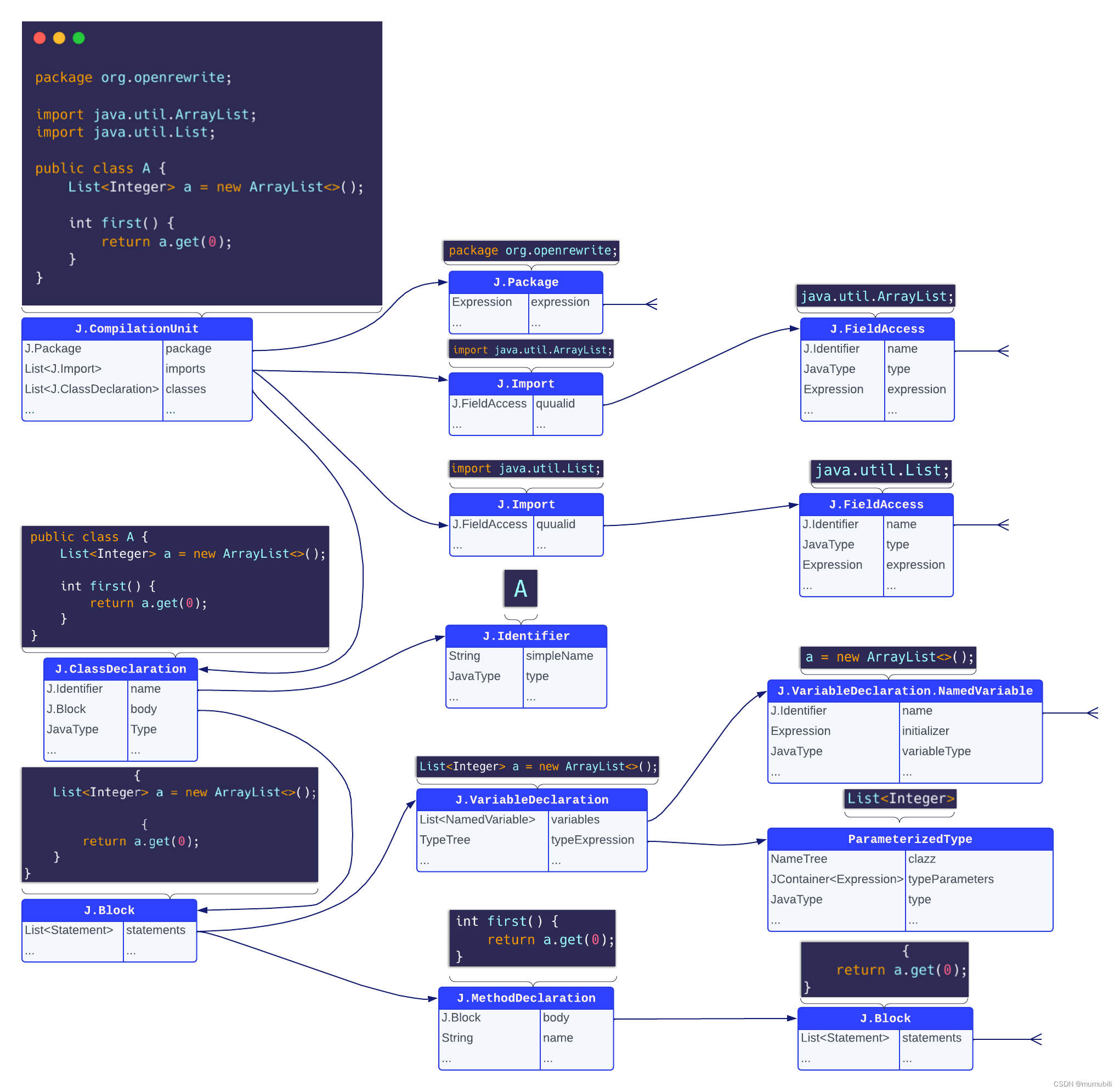
目录

迪杰斯特拉模板（用来求一个点出发到其它点的最短距离）：

克鲁斯卡尔模板（用来求最小生成树）：

题目一（蓝桥王国）：

题目二（随机数据下的最短路径）： 

题目三（出差）：

题目四（聪明的猴子）：

 题目六（机房）：

迪杰斯特拉模板（用来求一个点出发到其它点的最短距离）：

#include<iostream>
#include<queue>
#include<vector>
#include<cstring>
using namespace std;
typedef long long ll;
const ll N = 3e5 + 10, M = 1e6 + 10, inf = 1e14;
struct  node
{
    ll v, w;
    bool operator <(const node& y) const//重载一个<,用于优先队列排序
    {
        return w > y.w;//小到大
    }
};
int n, m;
priority_queue<node>q;
vector<node> e[N];
ll dis[N], vis[N];
void Dij()
{
    dis[1] = 0;//从1号点出发，表示从1到1距离为0
    q.push({ 1,dis[1] });//1号点以及到1的距离入队
    while (q.size())
    {
        int u = q.top().v;//取最小边相连的点出队
        q.pop();
        if (vis[u])//访问过则跳过
            continue;
        vis[u] = 1;//没访问赋为访问
        for (auto i : e[u])//遍历以u为出发点的边
        {
            int v = i.v, w = i.w;//取其相连的点及权值
            if (dis[v] > dis[u] + w)//经过u点到v点的权值小于之前的权值则更新
            {
                dis[v] = dis[u] + w;
                q.push({ v,dis[v] });//v点以及到v的距离
            }
        }
    }

}
int main()
{
    cin >> n >> m;
    fill(dis+1, dis+1+n, inf);//赋值一个无穷大，表示没有连接
    for (int i = 1; i <= m; i++)
    {
        int x, y, w;
        cin >> x >> y >> w;
        e[x].push_back({ y,w });//存入以x出发到y，权值为w
    }
    Dij();
}

克鲁斯卡尔模板（用来求最小生成树）：

#include<iostream>
#include<vector>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 1e3+20;
int m, n;
int h[N],f[N],x[N],y[N];
struct edge
{
    int v1, v2;
    double w;
};
vector<edge> e;
int find(int k)//查找
{
    if (f[k] == k)
        return k;
    return f[k] = find(f[k]);
}
void  merge(int x, int y)//合并
{
  x=find(x),y=find(y);
    if (x!= y)
        f[x] = f[y];
}
bool cmp(edge a, edge b)
{
    return a.w < b.w;
}
int main()
{
    cin >> n;
    for (int j = 1; j <= n; j++)
    {
        cin >> x[j] >> y[j]>> h[j];
        f[j] = j;//初始化并查集根
    }
    for(int i=1;i<=n;i++)
        for (int j = i + 1; j <= n; j++)//添加边
        {
            int w;
            cin>>w;
            e.push_back({ i, j, w });
        }
    sort(e.begin(), e.end(), cmp);//边从小到大排序
    int cnt=0;
    for (int i = 0; i < e.size(); i++)
    {
        if (find(e[i].v1) != find(e[i].v2))//不属于一个集合
        {
            merge(e[i].v1, e[i].v2);//合并
        }
        if (cnt == n-1)//n个点只需要n-1条边，选取n-1条边后，跳出循环
            break;
    }
}

题目一（蓝桥王国）：

#include<iostream>
#include<queue>
#include<vector>
#include<cstring>
using namespace std;
typedef long long ll;
const ll N = 3e5 + 10, M = 1e6 + 10, inf = 1e14;
struct  node
{
    ll v, w;
    bool operator <(const node& y) const//重载一个<,用于优先队列排序
    {
        return w > y.w;//小到大
    }
};
int n, m;
priority_queue<node>q;
vector<node> e[N];
ll dis[N], vis[N];
void Dij()
{
    dis[1] = 0;//从1号点出发，表示从1到1距离为0
    q.push({ 1,dis[1] });//1号点以及到1的距离入队
    while (q.size())
    {
        int u = q.top().v;//取最小边相连的点出队
        q.pop();
        if (vis[u])//访问过则跳过
            continue;
        vis[u] = 1;//没访问赋为访问
        for (auto i : e[u])//遍历以u为出发点的边
        {
            int v = i.v, w = i.w;//取其相连的点及权值
            if (dis[v] > dis[u] + w)//经过u点到v点的权值小于之前的权值则更新
            {
                dis[v] = dis[u] + w;
                q.push({ v,dis[v] });//v点以及到v的距离
            }
        }
    }

}
int main()
{
    cin >> n >> m;
    fill(dis+1, dis+1+n, inf);//赋值一个无穷大，表示没有连接
    for (int i = 1; i <= m; i++)
    {
        int x, y, w;
        cin >> x >> y >> w;
        e[x].push_back({ y,w });//存入以x出发到y，权值为w
    }
    Dij();
    for (int i = 1; i <= n; i++)
    {
        if (dis[i] >= inf)//无法到达
            cout << -1 << " ";
        else
            cout << dis[i] << " ";
    }
}

题目二（随机数据下的最短路径）： 

 

#include<iostream>
#include<queue>
#include<vector>
#include<cstring>
using namespace std;
typedef long long ll;
const ll N = 3e5 + 10, M = 1e6 + 10, inf = 1e14;
struct  node
{
    ll v, w;
    bool operator <(const node& y) const//重载一个<,用于优先队列排序
    {
        return w > y.w;//小到大
    }
};
int n, m, t;
priority_queue<node>q;
vector<node> e[N];
ll dis[N], vis[N];
void Dij(int t)
{
    dis[t] = 0;//从t号点出发，表示从t到t距离为0
    q.push({ t,dis[t] });//t号点以及到t的距离入队
    while (q.size())
    {
        int u = q.top().v;//取最小边相连的点出队
        q.pop();
        if (vis[u])//访问过则跳过
            continue;
        vis[u] = 1;//没访问赋为访问
        for (auto i : e[u])//遍历以u为出发点的边
        {
            int v = i.v, w = i.w;//取其相连的点及权值
            if (dis[v] > dis[u] + w)//经过u点到v点的权值小于之前的权值则更新
            {
                dis[v] = dis[u] + w;
                q.push({ v,dis[v] });//v点以及到v的距离
            }
        }
    }

}
int main()
{
    cin >> n >> m>> t;
    fill(dis+1, dis+1+n, inf);//赋值一个无穷大，表示没有连接
    for (int i = 1; i <= m; i++)
    {
        int x, y, w;
        cin >> x >> y >> w;
        e[x].push_back({ y,w });//存入以x出发到y，权值为w
    }
    Dij(t);//从t点出发
    for (int i = 1; i <= n; i++)
    {
        if (dis[i] == inf)//无法到达
            cout << -1 << " ";
        else
            cout << dis[i] << " ";
    }
}

题目三（出差）：

#include<iostream>
#include<queue>
#include<vector>
#include<cstring>
using namespace std;
typedef long long ll;
const ll N = 3e5 + 10, M = 1e6 + 10, inf = 1e14;
struct  node
{
	int v, w;
	bool operator <(const node& y) const//重载一个<,用于优先队列排序
	{
		return w > y.w;//小到大
	}
};
int n, m;
priority_queue<node>q;
vector<node> e[N];
int dis[N], vis[N], time0[N];
void Dij()
{
	dis[1] = 0;//从1号点出发，表示从1到1距离为0
	q.push({ 1,dis[1] });//1号点以及到1的距离入队
	while (q.size())
	{
		int u = q.top().v;//取最小边相连的点出队
		q.pop();
		if (vis[u])//访问过则跳过
			continue;
		vis[u] = 1;//没访问赋为访问
		for (auto i : e[u])//遍历以u为出发点的边
		{
			int v = i.v, w = i.w;//取其相连的点及权值
			if (dis[v] > dis[u] + w)//经过u点到v点的权值小于之前的权值则更新
			{
				dis[v] = dis[u] + w;
				q.push({ v,dis[v] });//v点以及到v的距离
			}
		}
	}
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
		cin >> time0[i];
	fill(dis + 1, dis + 1 + n, inf);//赋值一个无穷大，表示没有连接
	for (int i = 1; i <= m; i++)
	{
		int x, y, w;
		cin >> x >> y >> w;
		e[x].push_back({ y,w + time0[y]});//存入以x出发到y，权值为w+隔离时间
		e[y].push_back({ x,w + time0[x] });//存入以y出发到y,权值为w+隔离时间
	}
	Dij();
	cout << dis[n] - time0[n];//要减掉最后终点的隔离时间
}

题目四（聪明的猴子）：

#include<iostream>
#include<vector>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 1e3+20;
int m, n;
int a[N],f[N],x[N],y[N];
struct edge
{
    int v1, v2;
    double w;
};
vector<edge> e;
int find(int k)//查找
{
    if (f[k] == k)
        return k;
    return f[k] = find(f[k]);
}
void  merge(int x, int y)//合并
{
  x=find(x),y=find(y);
    if (x!= y)
        f[x] = f[y];
}
bool cmp(edge a, edge b)
{
    return a.w < b.w;
}
int main()
{
    cin >> m;
    for (int i = 1; i <= m; i++)
        cin >> a[i];
    cin >> n;
    for (int j = 1; j <= n; j++)
    {
        cin >> x[j] >> y[j];
        f[j] = j;//初始化并查集根
    }
    for(int i=1;i<=n;i++)
        for (int j = i + 1; j <= n; j++)//添加边
        {
            double w = sqrt((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j]));
            e.push_back({ i, j, w });
        }
    sort(e.begin(), e.end(), cmp);//边从小到大排序
    double maxw = 0.0;//记录最小生成树中最大边
    int cnt = 0;
    for (int i = 0; i < e.size(); i++)
    {
        if (find(e[i].v1) != find(e[i].v2))//不属于一个集合
        {
            merge(e[i].v1, e[i].v2);//合并
            cnt++;
            maxw = max(maxw, e[i].w);//更新最小生成树中最大边
        }
        if (cnt == n-1)//n个点只需要n-1条边，选取n-1条边后，跳出循环
            break;
    }
    int ans = 0;
    for (int i = 1; i <= m; i++)
    {
        if (a[i] >= maxw)//有几只猴子大于最小生成树中最大边
            ans++;
    }
    cout << ans;
}

题目五（通电）：

#include<iostream>
#include<vector>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 1e3+20;
int m, n;
int h[N],f[N],x[N],y[N];
struct edge
{
    int v1, v2;
    double w;
};
vector<edge> e;
int find(int k)//查找
{
    if (f[k] == k)
        return k;
    return f[k] = find(f[k]);
}
void  merge(int x, int y)//合并
{
  x=find(x),y=find(y);
    if (x!= y)
        f[x] = f[y];
}
bool cmp(edge a, edge b)
{
    return a.w < b.w;
}
int main()
{
    cin >> n;
    for (int j = 1; j <= n; j++)
    {
        cin >> x[j] >> y[j]>> h[j];
        f[j] = j;//初始化并查集根
    }
    for(int i=1;i<=n;i++)
        for (int j = i + 1; j <= n; j++)//添加边
        {
            double w = sqrt((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j]))+(h[i]-h[j])*(h[i]-h[j]);
            e.push_back({ i, j, w });
        }
    sort(e.begin(), e.end(), cmp);//边从小到大排序
    double maxw = 0.0;//记录最小生成树中最大边
    double ans=0;
    int cnt=0;
    for (int i = 0; i < e.size(); i++)
    {
        if (find(e[i].v1) != find(e[i].v2))//不属于一个集合
        {
            merge(e[i].v1, e[i].v2);//合并
            ans+=e[i].w;//求和
            maxw = max(maxw, e[i].w);//更新最小生成树中最大边
        }
        if (cnt == n-1)//n个点只需要n-1条边，选取n-1条边后，跳出循环
            break;
    }
    printf("%.2lf",ans);
}

 题目六（机房）：

 

#include<iostream>
#include<queue>
#include<vector>
#include<cstring>
using namespace std;
typedef long long ll;
const ll N = 3e5 + 10, M = 1e6 + 10;
struct  node
{
    ll v, w;
    bool operator <(const node& y) const//重载一个<,用于优先队列排序
    {
        return w > y.w;//小到大
    }
};
int n, m;
priority_queue<node>q;
vector<node> e[N];
vector<node> temp;
ll dis[N], vis[N], cnt[N];
ll Dij(int u, int end)
{
    memset(vis, 0, sizeof(vis));
    memset(dis, 0x3f3f, sizeof(dis));
    dis[u] = 0;//从u号点出发，表示从u到u距离为0
    q.push({ u,dis[u] });//u号点以及到u的距离入队
    while (q.size())
    {
        int u = q.top().v;//取最小边相连的点出队
        q.pop();
        if (vis[u])//访问过则跳过
            continue;
        vis[u] = 1;//没访问赋为访问
        for (auto i : e[u])//遍历以u为出发点的边
        {
            int v = i.v, w = i.w;//取其相连的点及权值
            if (dis[v] > dis[u] + w)//经过u点到v点的权值小于之前的权值则更新
            {
                dis[v] = dis[u] + w;
                q.push({ v,dis[v] });//v点以及到v的距离
            }
        }
    }
    return dis[end]+cnt[end];//还需要加上自身延迟
}
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n - 1; i++)
    {
        int x, y;
        cin >> x >> y;
        cnt[x]++, cnt[y]++;
        temp.push_back({ x,y });//临时存两个顶点
    }
    for (int i = 0; i < n - 1; i++)//根据度构造边
    {
        int u = temp[i].v, v = temp[i].w;
        e[u].push_back({ v,cnt[u] });//u->v的边，权值为u的度
        e[v].push_back({ u,cnt[v] });
    }
    while (m--)//m次查询
    {
        int u, v;
        cin >> u >> v;
        if (u == v)
            cout << cnt[u] << endl;
        else
        {
            ll ans = Dij(u, v);
            cout << ans << endl;
        }
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1511869.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Hadoop学习2：完全分布集群搭建

Hadoop学习2：完全分布集群搭建

文章目录 Fully-Distributed Operation&#xff08;完全分布模式&#xff09; 重点机器环境同步集群规划配置文件修改以及同步步骤0&#xff1a;下面其他步骤涉及修改配置以这里为准&#xff08;要不然部署使用过程会有很多问题&#xff09;通用配置&#xff08;三台节点机器&a…
阅读更多...
社交革命的引领者：探索Facebook如何改变我们的生活方式

社交革命的引领者：探索Facebook如何改变我们的生活方式

1.数字社交的兴起 随着互联网的普及&#xff0c;社交媒体成为我们日常生活的重要组成部分。Facebook作为其中的先驱&#xff0c;从最初的社交网络演变成了一个拥有数十亿用户的全球化平台。它不仅改变了我们与世界互动的方式&#xff0c;还深刻影响了我们的社交习惯、人际关系以…
阅读更多...
华为机考：HJ102 字符统计

华为机考：HJ102 字符统计

华为机考&#xff1a;HJ102 字符统计 描述 方法1 先将所有字符计算数量&#xff0c;在对比其中字符的assic码 #include<iostream> #include<vector> #include<algorithm> #include<string> using namespace std; bool cmp(pair<char, int> a,…
阅读更多...
C++ std::list的merge()使用与分析

C++ std::list的merge()使用与分析

看到《C标准库第2版》对list::merge()的相关介绍&#xff0c;令我有点迷糊&#xff0c;特意敲代码验了一下不同情况的调用结果。 《C标准库第2版》对list::merge()的相关介绍 list::merge()定义 merge()的作用就是将两个list合并在一起&#xff0c;函数有2个版本&#xff1a;…
阅读更多...
数字图像处理-空间滤波

数字图像处理-空间滤波

空间滤波 空域滤波基础 – 离散卷积的边缘效应 平滑空间滤波器 # -*- coding: utf-8 -*- # Author: Huazhong Yang # Email: cjdxyhz163.com # Time : 2024/3/7 20:26import cv2 import numpy as np# 读取图像 image cv2.imread(a1.png)# 应用高斯滤波 # 第二个参数是高斯…
阅读更多...
微信小程序开发系列（三十）·小程序本地存储API·同步和异步的区别

微信小程序开发系列（三十）·小程序本地存储API·同步和异步的区别

目录 1. 同步API 1.1 getStorageSync存储API 1.2 removeStorageSync获取数据API 1.3 removeStorageSync删除 1.4 clearStorageSync清空 2. 异步API 2.1 setStorage存储API 2.2 getStorage获取数据API 2.3 removeStorage删除API 2.4 clearStorage清空 3. …
阅读更多...
qt vs 编程 字符编码 程序从源码到编译到显示过程中存在的字符编码

qt vs 编程 字符编码 程序从源码到编译到显示过程中存在的字符编码

理解字符编码&#xff0c;请参考&#xff1a;unicode ucs2 utf16 utf8 ansi GBK GB2312 CSDN博客 汉字&#xff08;或者说多字节字符&#xff09;的存放需求&#xff0c;是计算机中各种编码问题的最直接原因。如果程序不直接使用汉字&#xff0c;或间接在所有操作步骤中统一使…
阅读更多...
Hilt

Hilt

1.使用Hilt实现快速依赖注入 1.1 导入依赖 //hilt依赖//Hiltimplementation("com.google.dagger:hilt-android:2.44")annotationProcessor("com.google.dagger:hilt-android-compiler:2.44")1.2 在build.gradle(app)中加入插件 plugins {id("com.an…
阅读更多...
大规模自动化重构框架--OpenRewrite浅析

大规模自动化重构框架--OpenRewrite浅析

目录 1. OpenRewrite是什么&#xff1f;定位&#xff1f; 2. OpenWrite具体如何做&#xff1f; 3. 核心概念释义 3.1 Lossless Semantic Trees (LST) 无损语义树 3.2 访问器&#xff08;Visitors&#xff09; 3.3 配方&#xff08;Recipes&#xff09; 4. 参考链接 Open…
阅读更多...
SpringBlade error/list SQL 注入漏洞复现

SpringBlade error/list SQL 注入漏洞复现

0x01 产品简介 SpringBlade 是一个由商业级项目升级优化而来的 SpringCloud 分布式微服务架构、SpringBoot 单体式微服务架构并存的综合型项目。 0x02 漏洞概述 SpringBlade 框架后台 /api/blade-log/error/list路径存在SQL注入漏洞，攻击者除了可以利用 SQL 注入漏洞获取数…
阅读更多...
Redis应用缓存

Redis应用缓存

目录 前言 关于“二八定律” 使用Redis作为缓存 为什么关系型数据库性能不高 为什么并发量高了就容易宕机 Redis就是一个用来作为数据库缓存的常见方案 缓存更新策略 定期生成 搜索引擎为例 实时生成 淘汰策略 FIFO(First In First Out) 先进先出 lRU(Least …
阅读更多...
106. Dockerfile通过多阶段构建减小Golang镜像的大小

106. Dockerfile通过多阶段构建减小Golang镜像的大小

我们如何通过引入具有多阶段构建过程的Dockerfiles来减小Golang镜像的大小&#xff1f; 让我们从一个通用的Dockerfile开始&#xff0c;它负责处理基本的事务&#xff0c;如依赖项、构建二进制文件、声明暴露的端口等&#xff0c;以便为Go中的一个非常基础的REST API提供服务。…
阅读更多...
YoloV8实战：YoloV8-World应用实战案例

YoloV8实战：YoloV8-World应用实战案例

摘要 YOLO-World模型确实是一个突破性的创新&#xff0c;它结合了YOLOv8框架的实时性能与开放式词汇检测的能力&#xff0c;为众多视觉应用提供了前所未有的解决方案。以下是对YOLO-World模型的进一步解读&#xff1a; 模型架构与功能 YOLO-World模型充分利用了YOLOv8框架的…
阅读更多...
剑指offer面试题34：在二叉树中和为某一值的路径

剑指offer面试题34：在二叉树中和为某一值的路径

面试题34&#xff1a;在二叉树中和为某一值的路径 题目&#xff1a; LCR 153. 二叉树中和为目标值的路径 - 力扣&#xff08;LeetCode&#xff09; 给你二叉树的根节点 root 和一个整数目标和 targetSum &#xff0c;找出所有 从根节点到叶子节点 路径总和等于给定目标和的路…
阅读更多...
C语言 - 各种自定义数据类型

C语言 - 各种自定义数据类型

1.结构体 把不同类型的数据组合成一个整体 所占内存长度是各成员所占内存的总和 typedef struct XXX { int a; char b; }txxx; txxx data; typedef struct XXX { int a:1; int b:1; …
阅读更多...
鸿蒙Harmony应用开发—ArkTS声明式开发（基础手势：RichText）

鸿蒙Harmony应用开发—ArkTS声明式开发（基础手势：RichText）

富文本组件&#xff0c;解析并显示HTML格式文本。 说明&#xff1a; 该组件从API Version 8开始支持。后续版本如有新增内容&#xff0c;则采用上角标单独标记该内容的起始版本。该组件无法根据内容自适应设置宽高属性&#xff0c;需要开发者设置显示布局。 子组件 不包含子组…
阅读更多...
封装的echarts子组件使用watch监听option失效的问题

封装的echarts子组件使用watch监听option失效的问题

项目场景&#xff1a; 我在项目里面封装了一个echarts组件&#xff0c;组件接收一个来自外部的option,然后我用了一个watch函数去监听这个option的变化&#xff0c;option变化之后&#xff0c;销毁&#xff0c;然后再新建一个charts表 碎碎念 问题如标题所示&#xff0c;这篇…
阅读更多...
ubuntu 安装 infiniband 和 RoCE 驱动

ubuntu 安装 infiniband 和 RoCE 驱动

下载驱动程序 驱动程序地址 https://network.nvidia.com/products/infiniband-drivers/linux/mlnx_ofed/ 安装 安装参考文档 https://docs.nvidia.com/networking/display/mlnxofedv24010331/installing+mlnx_ofed#src-2571322208_InstallingMLNX_OFED-InstallationProced…
阅读更多...
十五、计算机视觉-sobel算子

十五、计算机视觉-sobel算子

文章目录 前言一、sobel算子的概念二、sobel算子的计算方式三、具体实现 前言 上节课我们学习了梯度的知识&#xff0c;学习了如何去计算梯度&#xff0c;本节我们继续学习计算梯度的方法&#xff0c;本节我们学习使用Sobel算子计算梯度&#xff0c;这与上节课梯度计算方法有所…
阅读更多...
Java客户端调用elasticsearch进行深度分页查询 （search_after）

Java客户端调用elasticsearch进行深度分页查询 （search_after）

Java客户端调用elasticsearch进行深度分页查询 &#xff08;search_after&#xff09; 一. 代码二. 测试结果 前言 这是我在这个网站整理的笔记,有错误的地方请指出&#xff0c;关注我&#xff0c;接下来还会持续更新。 作者&#xff1a;神的孩子都在歌唱 具体的Search_after解…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023