目录

2.4.1 传统的集合运算 （二目运算）

（1） 并（Union）

（2）差（Except）

（3） 交（Intersection）

（4） 笛卡尔积

2.4.2 专门的关系运算

专门的关系运算：几个记号

专门的关系运算

1.选择

2. 投影（Projection）

3. 连接（Join）

连接：等值连接

自然连接

悬浮元组（Dangling tuple）

外连接（Outer Join）

4. 除运算（Division）

---

关系代数是一种抽象的查询语言，它用对关系的运算来表达查询。关系代数运算对象是关系，运算结果也是关系，关系代数的运算符有两类：集合运算符和专门的关系运算符。

传统的集合运算是从关系的“水平”方向，即行的角度进行。专门的关系运算不仅涉及行而且涉及列。比较运算符和逻辑运算符用来辅助专门的关系运算符进行操作。

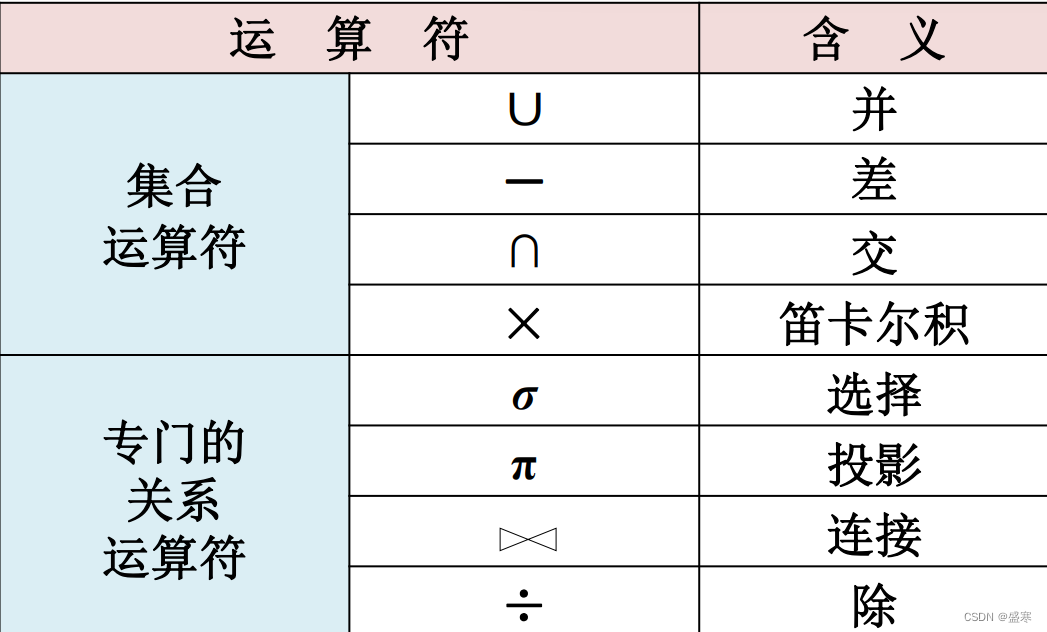
2.4.1 传统的集合运算 （二目运算）

前提（交并差）：设关系R和关系S具有相同的目  n（即两个关系都有n个属性），且相应的属性取自同一个域，𝑡 是元组变量， 𝑡 ∈ 𝑅 表示𝑡是R的一个元组。

（1） 并（Union）

 关系R和关系S的并记作：

  。

结果：仍为n目关系，由属于R或属于S的元组组成。

注意，并非R或S属性都必须相同，只要取在同一个域中即可。而组成的列数应还为n（依然为n目关系）。

（2）差（Except）

 R - S :关系R和关系S的差记作：

仍为n目关系，由属于R而不属于S的所有元组组成。

（3） 交（Intersection）

  R∩S：关系R和关系S的交记作：

仍为n目关系，由既属于R又属于S的元组组成，R ∩ S = R – ( R - S ）。

（4） 笛卡尔积

和我们之前章节中提到的笛卡尔积相同。

2.4.2 专门的关系运算

专门的关系运算：几个记号

先引入几个记号

（1）R, t∈R ,   

设关系模式为 R(A1，A2，…，An )

它的一个关系设为R

t∈R表示t是R的一个元组

t[Ai ]则表示元组t中相应于属性Ai的一个分量。

（2）

可以参照集合的思想来理解。

（3）

（4）

给定一个关系R（X，Z），X和Z为属性组。

当t[X]=x时，x在R中的象集（Images Set）为： Zx ={t[Z]|t ∈ R，t[X]=x}

表示R中属性组X上值为x的诸元组在Z上分量的集合。

举例：

专门的关系运算

1.选择

含义：在关系R中选择满足给定条件的诸元组。

记做：

选择条件是一个逻辑表达式，取值为“真”或“假”。

基本形式为：X1 θ Y1

θ表示比较运算符，它可以是＞，≥，＜，≤，＝或<>

X1，Y1是属性名，或者常量，或者简单函数

在基本的选择条件上，还可以用逻辑运算符非¬，与∧，或∨ 连接各条件表达式。（涉及多个条件的情况）

理解为在表内查询符合条件 f 的一整个（或多个）元组（行）

选择运算是从关系R中选取使逻辑表达式F为真的元组，是从行的角度进行的运算。

2. 投影（Projection）

含义：从R中选择出若干属性列组成新的关系

记作：

A：R中的属性列

投影操作主要是从列的角度进行运算。

投影之后不仅取消了原关系中的某些列，因为取消了某些列，可能出现重复的行，应取消这些重复元组。（之所以出现重复行是因为投影所造成的信息丢失）。

3. 连接（Join）

也称为θ连接

含义：从两个关系的笛卡尔积中选取属性间满足一定条件的元组。

连接运算从R和S的广义笛卡尔积R×S中选取R关系在A属性组上的值与S关系在B属性组上的值满足比较关系θ的元组。

理解：在笛卡尔积张成的空间中选取符合条件的列，和选择有些像但是选择是单表，而笛卡尔积是进行两表的交互。

连接：等值连接

两类常用连接运算：等值连接，自然连接。

自然连接

自然连接是一种特殊的等值连接

两个关系中进行比较的分量必须是同名的属性组

在结果中把重复的属性列去掉。

一般连接操作是从行的角度进行运算，自然连接还需要取消重复列，是同时进行行和列的运算。

悬浮元组（Dangling tuple）

两个关系R和S在做自然连接时，关系R中某些元组有可能在S中不存在公共属性上值相等的元组，从而造成R中这些元组在操作时被舍弃了，这些被舍弃的元组称为悬浮元组。

外连接（Outer Join）

如果把悬浮元组也保存在结果关系中，而在其他属性上填空值 (Null)，称为外连接。

左外连接(LEFT OUTER JOIN或LEFT JOIN)，只保留左边关系R中的悬浮元组。右外连接(RIGHT OUTER JOIN或RIGHT JOIN)，只保留右边关系S中的悬浮元组。

4. 除运算（Division）

定义：给定关系𝑅(𝑋, 𝑌) 和𝑆(𝑌, 𝑍) ，其中𝑋, 𝑌, 𝑍为属性组。R中的Y与S 中的Y可以有不同的属性名，但必须出自相同的域集。

R与S的除运算得到一个新的关系P(X)，P 是 R 中满足下列条件的元组在 X 属性列上的投影：元组在X上分量值𝑥的象集𝑌𝑥包含S在Y上投影的集合。

记做：

含义：设关系R除以关系S的结果为关系T，则T包含所有在R中但不在S中的属性及其值，且T的元组与S的元组的所有组合都在R中。

运用：解决“至少”的问题，首先我们被除数所得象集必须包含除数，因此我们得到的结果的组的象集是“至少”问题的答案。