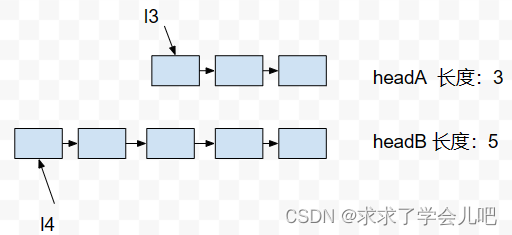
1.两重二for循环+维护次大值
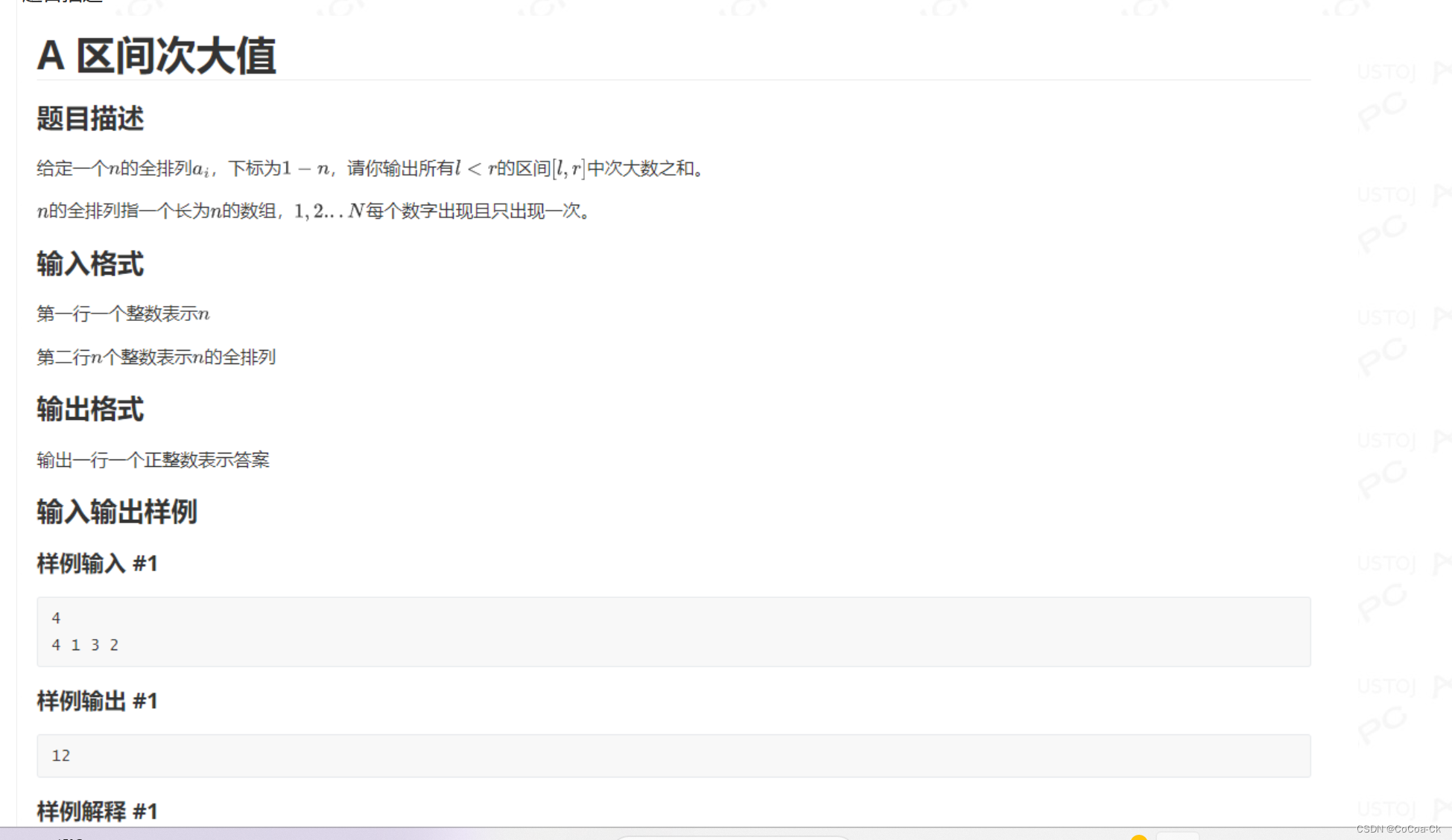
这里我就直接用map维护了,多了个logn复杂度还是可以的,下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,a[1010];
map<int,int> mp;
int main(){
cin>>n;
int sum=0;
map<int,int>::iterator it;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n-1;i++){
mp.clear();
mp[a[i]]=1;
for(int j=i+1;j<=n;j++){
mp[a[j]]=1;
it=mp.end();
it--;
it--;
sum+=(it->first);
}
mp.erase(a[i]);
}
cout<<sum;
} 2.二分查找+迪杰斯特拉:

显然,我们考虑每一次遍历时的最大体力值a,若a可以,那么比a大的肯定也可,满足单调性。
我们在每次二分时按照体力建图跑个迪杰斯特拉即可,下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,h,w,cnt,head[10101],st,ed,a[10101],max1,min1,ss;
bool vis[10010];
struct node{
int dian,next,zhi;
}edge[40006];
int xx[20006],yy[20006],ww[20006];
int dis[10101];
void merge(int u,int v,int bb){
edge[++cnt].dian=v;
edge[cnt].next=head[u];
edge[cnt].zhi=bb;
head[u]=cnt;
}
struct ty{
int dian,dis1;
bool operator<(const ty &a) const{
return dis1>a.dis1;
}
};
priority_queue<ty> q;
int dij(int s,int t){
q.push({s,0});
while(!q.empty()){
ty ck=q.top();
q.pop();
if(vis[ck.dian]) continue;
vis[ck.dian]=1;
for(int i=head[ck.dian];i!=-1;i=edge[i].next){
int i1=edge[i].dian;
if(vis[i1]) continue;
if(dis[i1]>dis[ck.dian]+edge[i].zhi){
dis[i1]=dis[ck.dian]+edge[i].zhi;
q.push({i1,dis[i1]});
}
}
}
if(dis[t]>=1e8) return -1;
else return dis[t];
}
bool check(int mid){
cnt=0;
memset(head,-1,sizeof(head));
memset(edge,0,sizeof(edge));
memset(vis,0,sizeof(vis));
for(int i=1;i<=m;i++){
if(a[xx[i]]>mid||a[yy[i]]>mid) continue;
merge(xx[i],yy[i],ww[i]);
merge(yy[i],xx[i],ww[i]);
}
memset(dis,0x7f7f7f7f,sizeof(dis));
dis[st]=0;
int yy=dij(st,ed);
if(yy==-1||yy>h) return 0;
else return 1;
}
int main(){
ios::sync_with_stdio(false);
cin>>n>>m>>st>>ed>>h;
for(int i=1;i<=n;i++){
cin>>a[i];
max1=max(max1,a[i]);
min1=min(min1,a[i]);
}
min1=max(a[st],min1);
min1=max(a[ed],min1);
for(int i=1;i<=m;i++) cin>>xx[i]>>yy[i]>>ww[i];
int i=min1,j=max1;
int f=0;
while(i<j){
int mid=(i+j)/2;
if(check(mid)){
f=1;
j=mid;
}
else i=mid+1;
}
if(f==0) cout<<-1;
else cout<<i;
}3.模拟:

按照字符串模拟即可,下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,sx,sy,l,dir[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
char a[5100][5100];
string s;
struct node{
int x,y;
}tr[2][40];
int main(){
ios::sync_with_stdio(false);
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++) cin>>a[i][j];
}
cin>>sx>>sy>>l>>s;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
char c=a[i][j];
if(c>='A'&&c<='Z'){
int qq=c-'A';
if(tr[0][qq].x==0&&tr[0][qq].y==0){
tr[0][qq].x=i;
tr[0][qq].y=j;
}
else{
tr[1][qq].x=i;
tr[1][qq].y=j;
}
}
}
}
for(int i=0;i<=s.length()-1;i++){
int x=sx,y=sy;
if(s[i]=='L') y--;
if(s[i]=='R') y++;
if(s[i]=='U') x--;
if(s[i]=='D') x++;
if(a[x][y]=='#') continue;
if(x<1||y<1||x>n||y>m) continue;
if(a[x][y]>='A'&&a[x][y]<='Z'){
int ww=a[x][y]-'A';
if(tr[0][ww].x==x&&tr[0][ww].y==y){
sx=tr[1][ww].x;
sy=tr[1][ww].y;
}
else{
sx=tr[0][ww].x;
sy=tr[0][ww].y;
}
}
else{
sx=x;
sy=y;
}
}
cout<<sx<<" "<<sy;
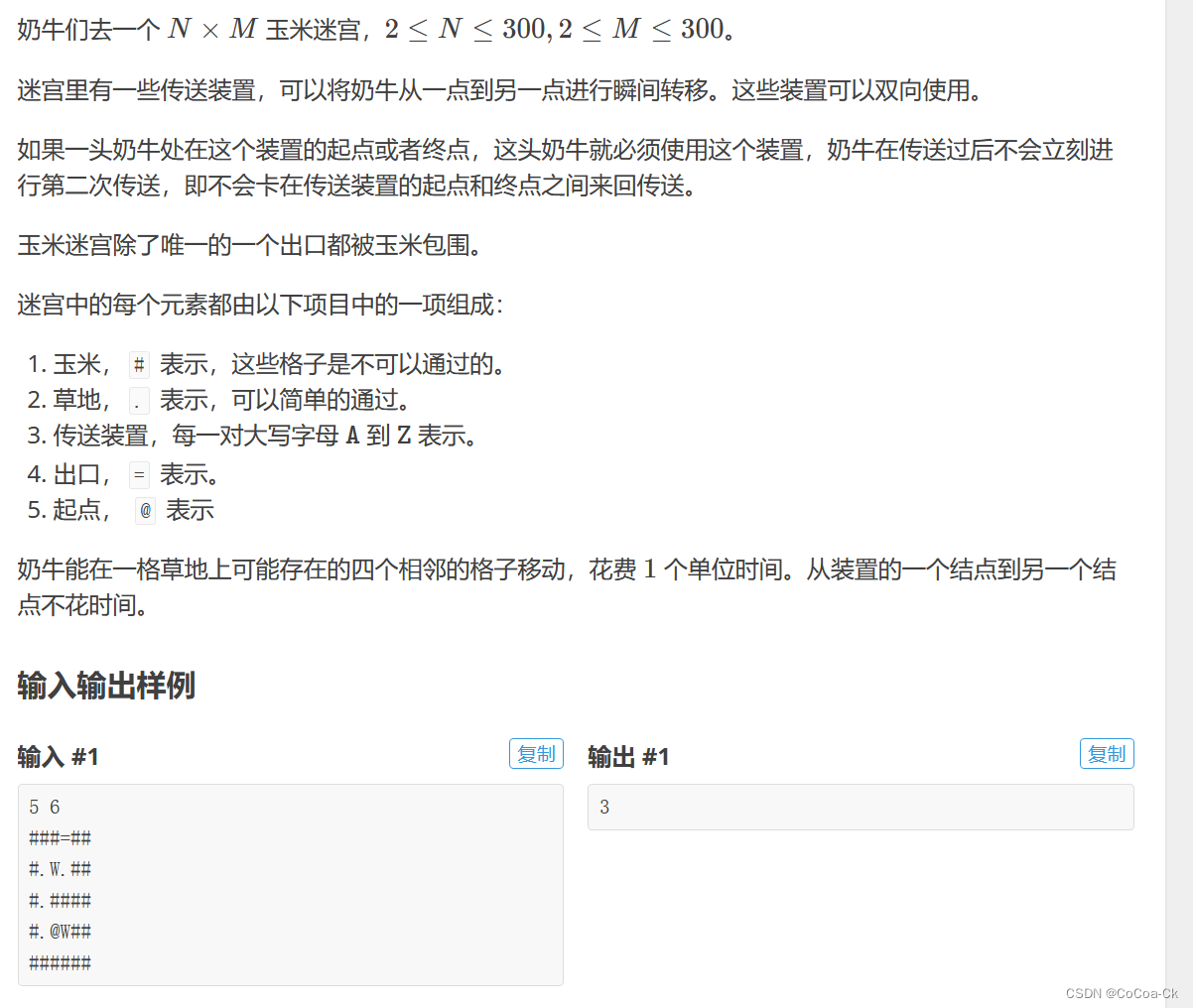
}4.BFS:

发现这道跟洛谷的一道类似,这里就懒一下放个以前洛谷上写的吧:
#include<bits/stdc++.h>
using namespace std;
int n,m,vis[400][400],stx,sty,edx,edy;
int dir[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
struct pos{
int x,y,t;
};
struct node{
int x,y;
}tr[2][40];
queue<pos> q;
char c,a[400][400];
bool check(int x,int y){
if(x<1||x>n||y<1||y>m||vis[x][y]==1||a[x][y]=='#') return 0;
return 1;
}
void bfs(){
q.push({stx,sty,0});
vis[stx][sty]=1;
while(!q.empty()){
pos ck=q.front();
q.pop();
int xx=ck.x,yy=ck.y;
if(xx==edx&&yy==edy){
cout<<ck.t;
return;
}
for(int i=0;i<4;i++){
int xxx=xx+dir[i][0];
int yyy=yy+dir[i][1];
if(check(xxx,yyy)==0) continue;
if(a[xxx][yyy]>'Z'||a[xxx][yyy]<'A'){
vis[xxx][yyy]=1;
q.push({xxx,yyy,ck.t+1});
}
else{
int ww=a[xxx][yyy]-'A';
if(tr[0][ww].x==xxx&&tr[0][ww].y==yyy){
q.push({tr[1][ww].x,tr[1][ww].y,ck.t+1});
}
else q.push({tr[0][ww].x,tr[0][ww].y,ck.t+1});
}
}
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>c;
a[i][j]=c;
if(c=='@'){
stx=i;
sty=j;
}
if(c=='='){
edx=i;
edy=j;
}
if(c>='A'&&c<='Z'){
int qq=c-'A';
if(tr[0][qq].x==0&&tr[0][qq].y==0){
tr[0][qq].x=i;
tr[0][qq].y=j;
}
else{
tr[1][qq].x=i;
tr[1][qq].y=j;
}
}
}
}
bfs();
}5.签到题(别被题面吓了)

取字符串最后一位即可。
6.斐波那契数列:

来个矩阵快速幂~~~:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int m,n,mod=1e9+7;
struct node{
int m[100][100];
}ans,res;
node mul(node a,node b){
node tmp;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
tmp.m[i][j]=0;
}
}
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
for(int k=0;k<n;k++){
tmp.m[i][j]=(tmp.m[i][j]+a.m[i][k]*b.m[k][j])%mod;
}
}
}
return tmp;
}
void quickpower(int m,int n){
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
if(i==j) ans.m[i][j]=1;
else ans.m[i][j]=0;
}
}
while(m){
if(m&1) ans=mul(ans,res);
res=mul(res,res);
m=m>>1;
}
}
signed main(){
cin>>m;
m-=2;
n=2;
res.m[0][0]=0;
res.m[1][0]=1;
res.m[1][1]=1;
res.m[0][1]=1;
if(m<0) cout<<1;
else {quickpower(m,n);
cout<<(ans.m[1][0]+ans.m[1][1])%mod;}
}7.(不会QAQ...)
8.DP:

我们令dp[i][j][k](k=0/1)表示取到第i个字符,前面转折次数<=j,最后一段是升/降的最长长度。
对于dp[i][j][1],我们遍历1--i-1作为第i个字符的前一个字符,如果比a[i]大,那么就可以直接接在dp[h][j][1]的后面,长度+1,否则可以多加一个转折dp[h][j-1][0]然后+1.对于dp[i][j][0]同理。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,k,dp[1010][1010][2],ans,a[1010];
int main(){
cin>>n>>k;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++){
for(int j=0;j<=k;j++){
dp[i][j][0]=1;
dp[i][j][1]=1;
for(int h=1;h<i;h++){
if(a[h]>a[i]){
dp[i][j][0]=max(dp[i][j][0],dp[h][j][0]+1);
if(j>=1) dp[i][j][0]=max(dp[i][j][0],dp[h][j-1][1]+1);
}
if(a[h]<a[i]){
dp[i][j][1]=max(dp[i][j][1],dp[h][j][1]+1);
if(j>=1) dp[i][j][1]=max(dp[i][j][1],dp[h][j-1][0]+1);
}
}
ans=max(ans,dp[i][j][0]);
ans=max(ans,dp[i][j][1]);
}
}
cout<<ans;
}9.模拟:
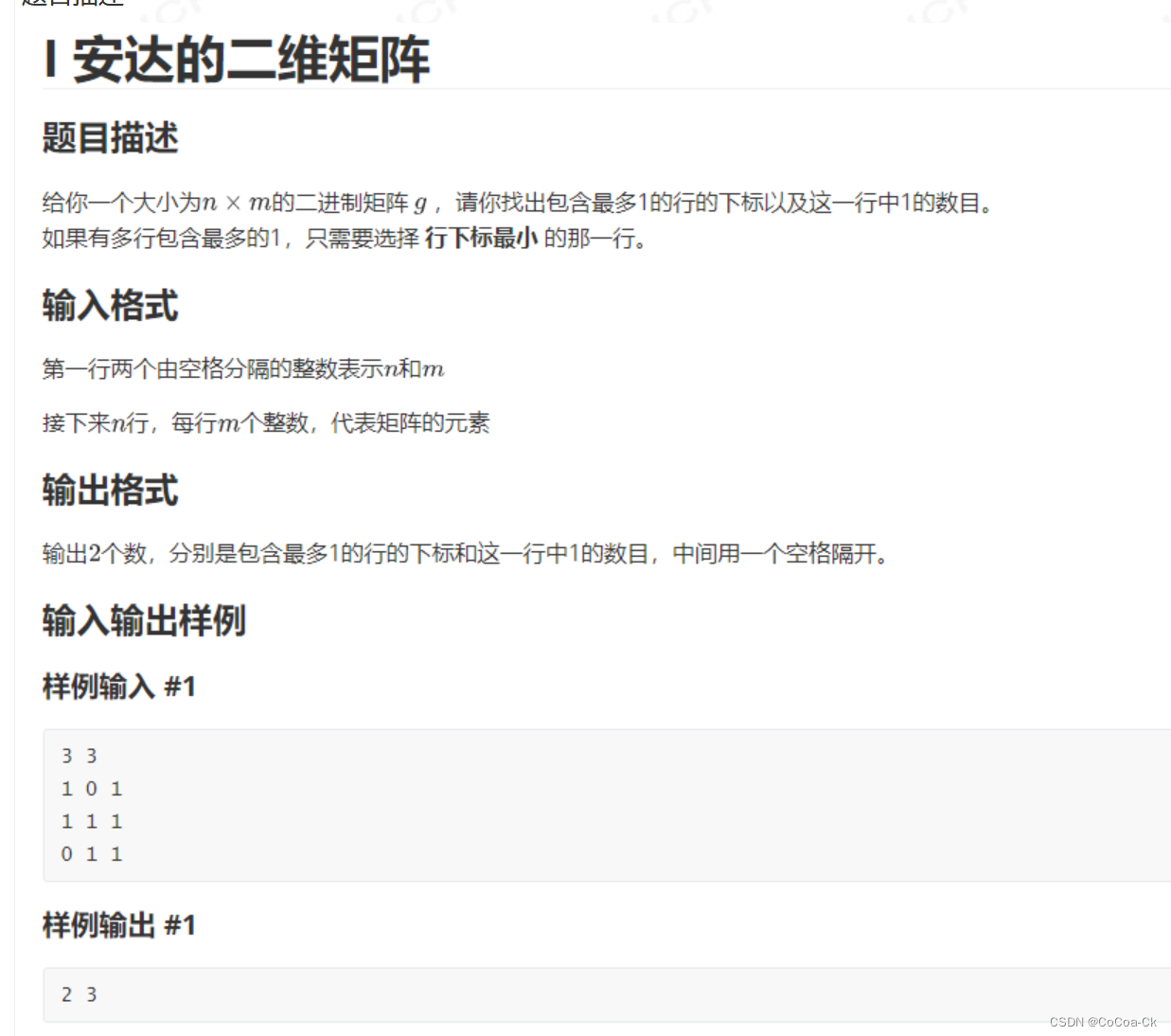
直接按题目意思模拟即可。
10.贪心:
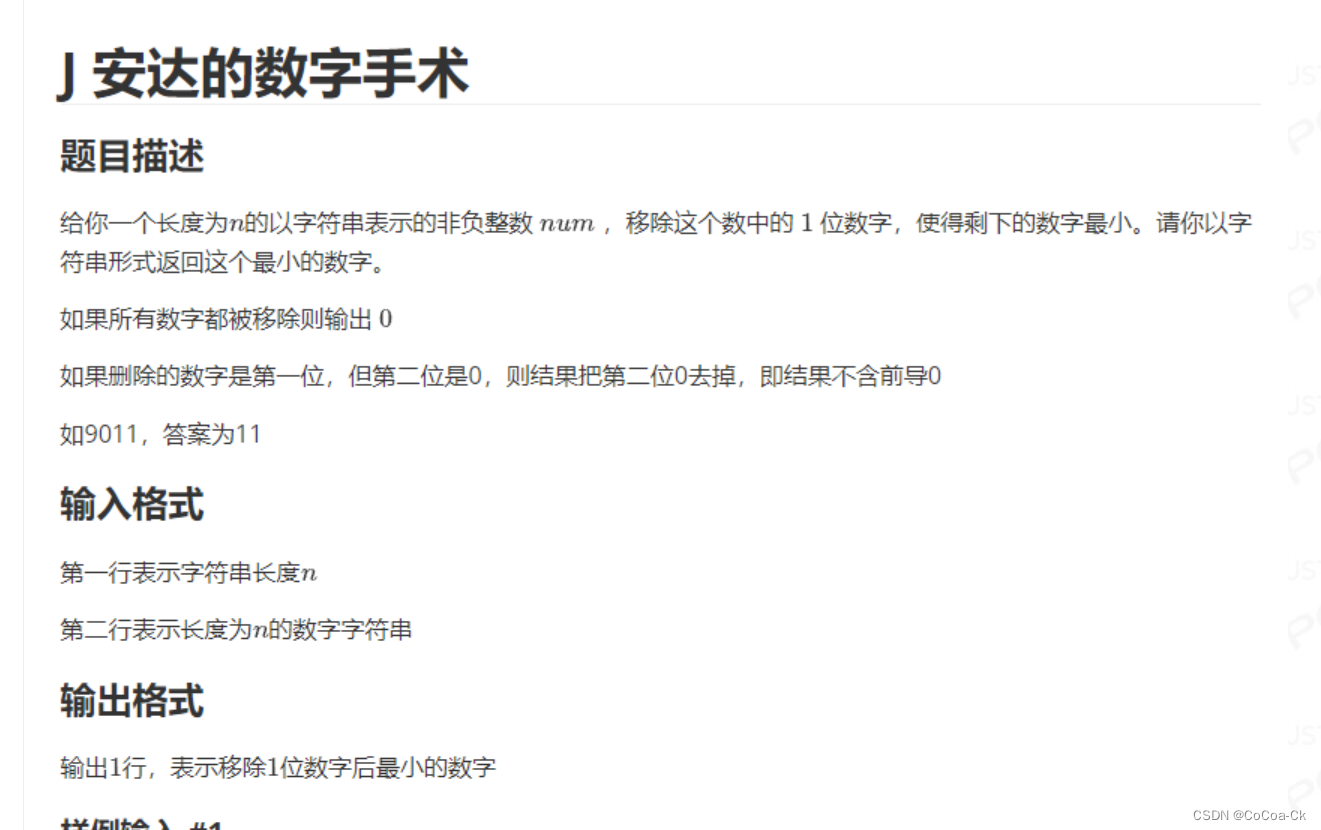
自己写几个找找规律,可以发现删序列出现递减的前一个数字即可,下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
char num[1000100],x;
bool a[1000100];
int n;
int main(){
cin>>n;
for(int i=0;i<=n-1;i++){
scanf(" %c",&x);
num[i]=x;}
if(n==1) cout<<0;
else if(n==2&&num[1]=='0') cout<<0;
else{
int f=0;
for(int i=0;i<n-1;i++){
if(num[i]>num[i+1]&&f==0){
f=1;
a[i]=1;
continue;
}
}
if(f==0) a[n-1]=1;
int kkk=0,cnt=0;
for(int i=0;i<=n-1;i++){
if(a[i]==1) continue;
if(kkk==0&&num[i]=='0') continue;
kkk=1;
cout<<num[i];
cnt++;
}
if(cnt==0) cout<<0;
}
}11.数学
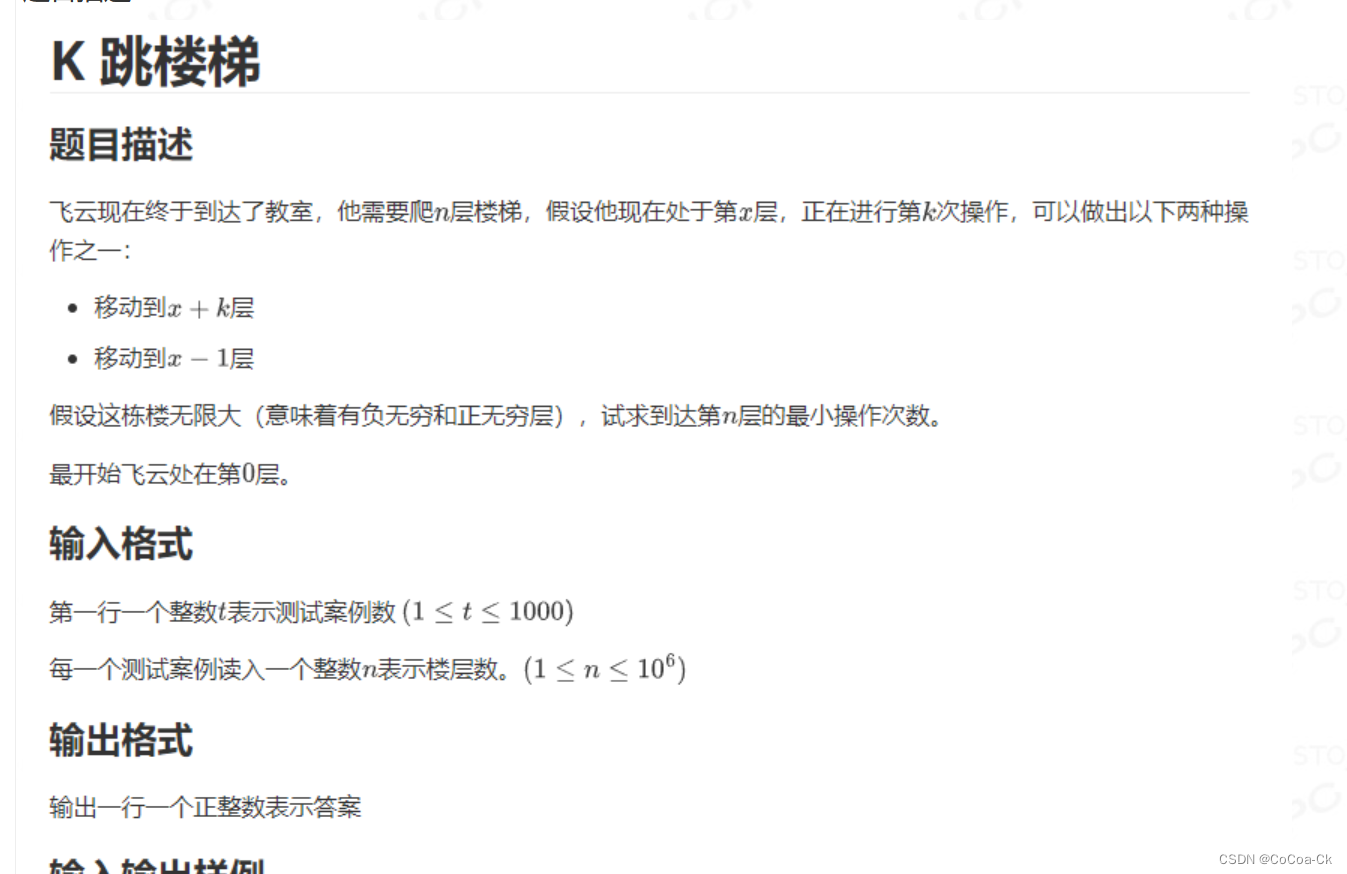
直接BFS就TLE了,我们发现我们按照1,3,6,10.。。取下去,若第一个数==答案或者-2>=答案,我们都可以通过吧一个数改成-1来实现,否则次数+1即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,k,t;
void solve(){
int sum=0,res=0;
for(int i=1;i<=2000;i++){
sum+=i;
if(sum==n||sum-1>n){
res=i;
break;
}
}
cout<<res;
}
int main(){
scanf("%d",&t);
while(t--){
scanf("%d",&n);
solve();
cout<<endl;
}
}12.前缀和+二分:
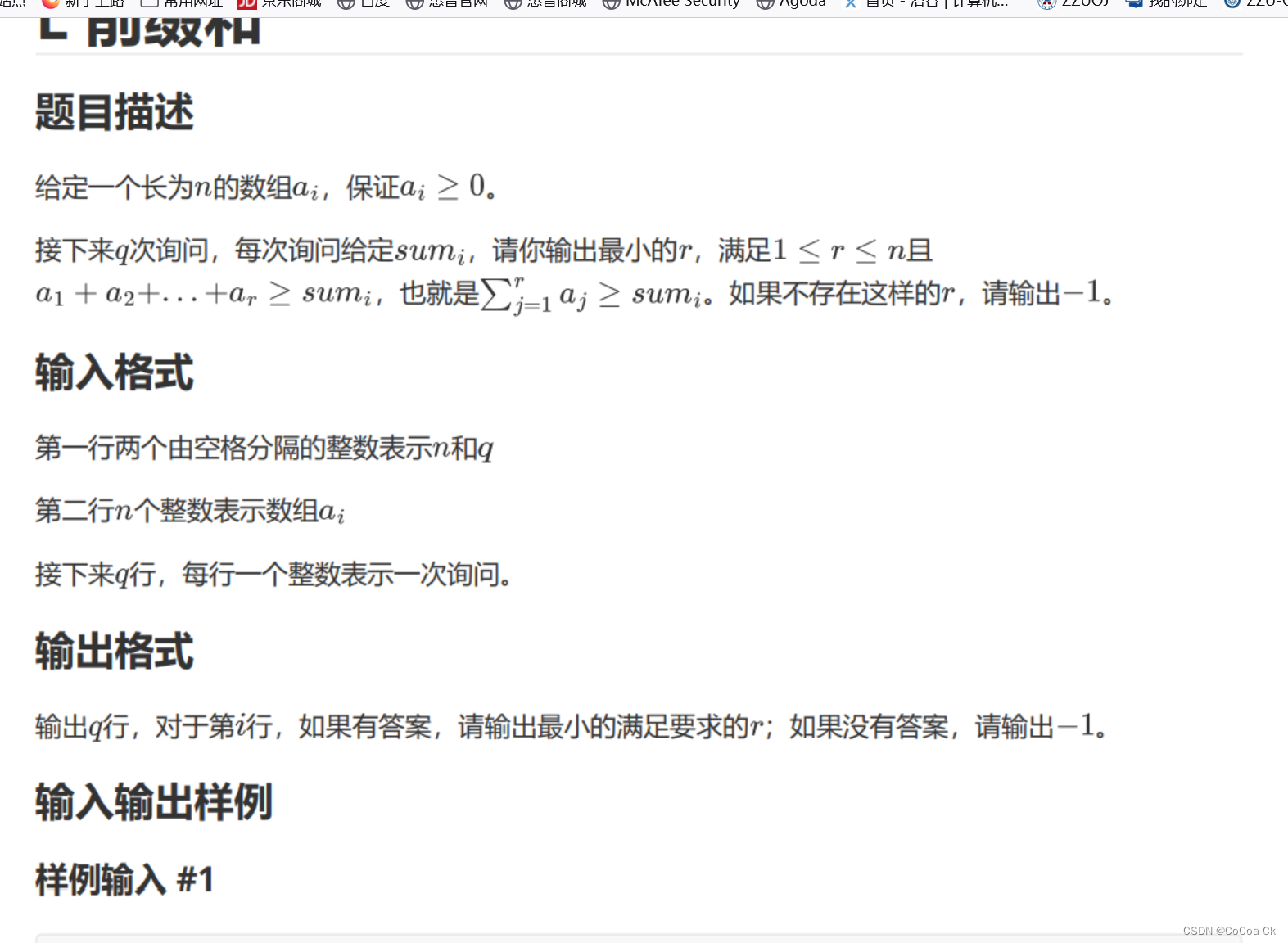
#include<bits/stdc++.h>
using namespace std;
int n,q,a[1000100];
long long sum;
long long ss[1000100];
int main(){
ios::sync_with_stdio(false);
cin>>n>>q;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) ss[i]=ss[i-1]+a[i];
for(int i=1;i<=q;i++){
cin>>sum;
int j=lower_bound(ss+1,ss+n+1,sum)-ss;
if(j==n+1) cout<<-1;
else printf("%d\n",j);
}
}