（ConvE）Convolutional 2D Knowledge Graph Embeddings

news2024/10/5 12:43:38

论文地址：https://arxiv.org/pdf/1707.01476.pdf

一、研究领域

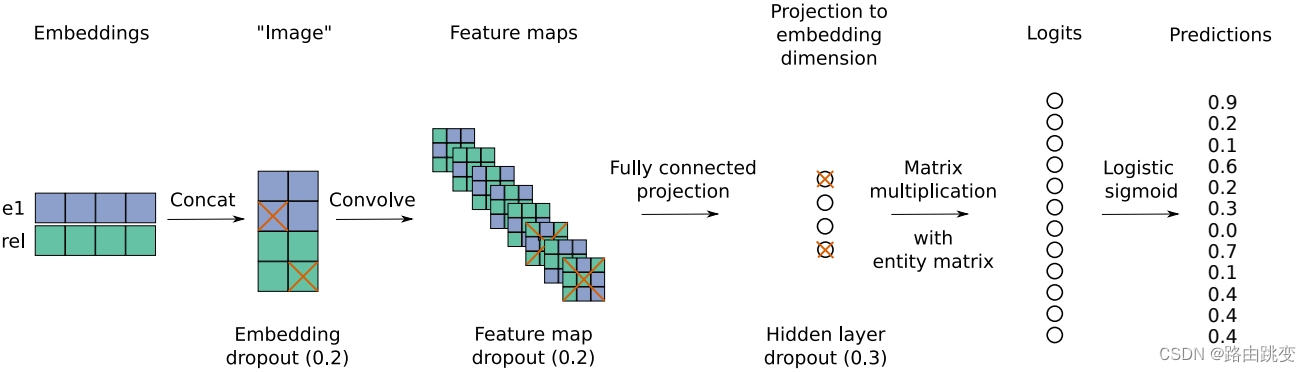
知识图谱受限于知识构建方式的不足，常常伴随着不完备的特点，因此需要知识推理和补齐技术，来根据已有的事实来合理推断出新的事实以补充知识图谱，使其更完备。链路预测任务是知识推理和补齐技术的主要手段，用于预测知识图谱中的实体之间是否存在缺失的关系边，从而达到扩充知识图谱的目的。本文提出的正是应用于知识推理链路预测任务的学习模型——ConvE。

二、论文动机

知识图谱可以包含百万数量级的事实三元组，因此为了应用到实际的生活场景上，链路预测器应该能以合理的方式扩展规模并且保持合适的参数量和计算复杂度。为了解决大规模应用的问题，链路预测模型总是由简单的操作组成，如内积和嵌入空间上的矩阵乘法，以及使用有限的参数，DistMult就是这样一种模型。使用这种简单、浅、快的模型使得其可以扩展到大规模知识图谱上，但付出了模型表达力不足、学习特征能力不足的代价。

而在浅层模型中增加特征数量使得模型更具表达力的唯一方法就是增加embedding的维度，但是这样做又会使得其不能扩展到大规模知识图谱上，因为嵌入参数的总数与知识图谱中实体和关系的数量是成正比的。例如，像DistMult这样的浅模型，当embedding的维度为200时，会使得应用到Freebase时需要33GB的内存来储存它的参数。

为了学习到更多的特征而又不增加embedding的大小需要使用多层的模型，然而，先前的多层知识图谱嵌入架构通常使用全连接层，这使得它们容易过拟合。解决以上问题的方法是使用可以组成深度网络的参数高效、快速的算子。现在考虑卷积（convolution）这个操作，常见于CV领域，它具有参数高效、计算快速的优点，并且由于其广泛的使用，当训练一个多层卷积网络的时候，有效解决它过拟合问题的方法也很多。因此，本文希望提出一个在embedding上使用二维卷积来实现链路预测的模型。