题目链接

[蓝桥杯 2020 省 B2] 平面切分

题目描述

平面上有 $N$ 条直线, 其中第 $i$ 条直线是 $y=A_i\cdot x+B_i$

请计算这些直线将平面分成了几个部分。

输入格式

第一行包含一个整数 $N$。

以下 $N$ 行, 每行包含两个整数 $A_i,B_i$。

输出格式

一个整数代表答案。

输入输出样例

输入

3
1 1
2 2
3 3

输出

6

数据范围

• $1\le N\le 1000$
• $10^{-5}\le A_i,B_i\le 10^5$

解法：计算几何 + 计数

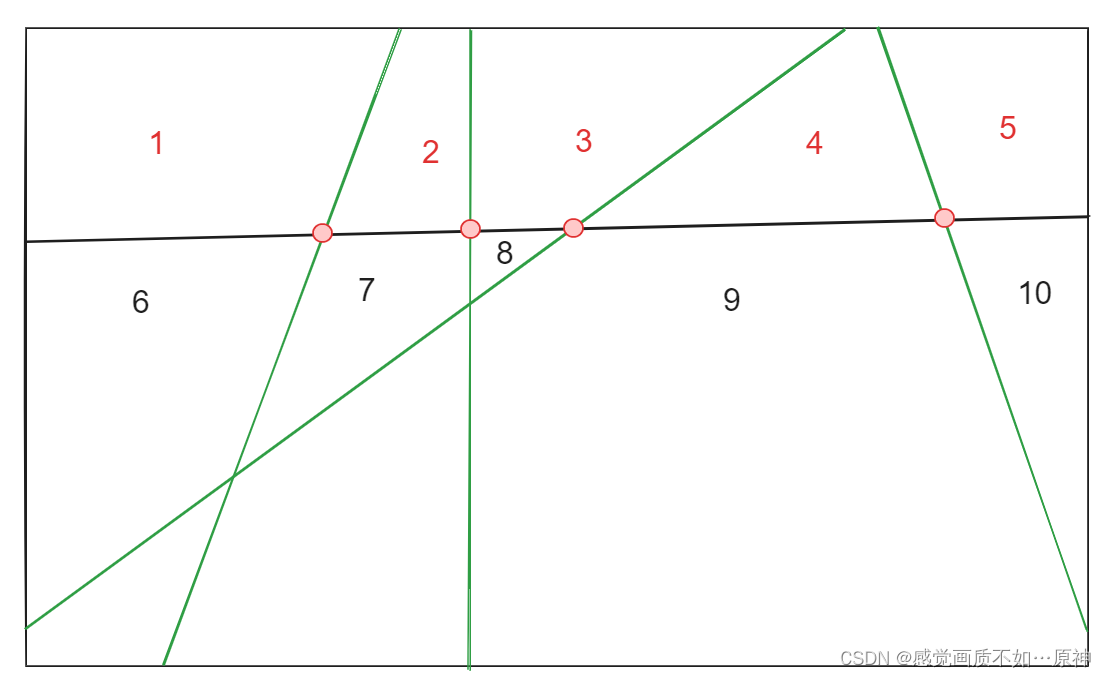
如上图，先有 $4$ 根绿色的线，然后又来了一根黑色的线，与之前绿色的线共有 $4$ 个交点。将原来的 $5$ 个部分，一分为二，即又新增了 $5$ 个部分（分别是 $1,2,3,4,5$）。

我们可以得出一个结论：如果新来的一条直线 与 已有的直线有 $t$ 个交点，那么就会增加 $t+1$ 个部分。

我们直接枚举每一条直线，与前面直线的交点即可。

注意：可能会出现重边的情况，所以需要去重！

时间复杂度：$O(n^2)$

C++代码：

#include <iostream>
#include <set>
#include <vector>

using namespace std;

using LD = long double;
using PII = pair<int,int>;

int main(){
    int n;
    cin>>n;
    
    vector<LD> k, b;
    set<PII> s;
    
    for(int i = 0;i < n;i++){
        int kk,bb;
        cin>>kk>>bb;
        s.insert(make_pair(kk,bb));
    }
    
    for(auto& [kk,bb]:s){
        k.push_back(kk);
        b.push_back(bb);
    }
    n = k.size();
    set<pair<LD,LD>> st;
    
    int ans = 2;
    for(int i = 1;i < n;i++){
        for(int j = i - 1;j >= 0;j--){
            if(k[i] == k[j]) continue; //两条边平行，肯定没有交点
            LD x = (b[i] - b[j]) / (k[j] - k[i]);
            LD y = k[i] * x + b[i];
            st.insert(make_pair(x, y));
        }
        ans += st.size() + 1;
        st.clear();
    }
    
    cout<<ans<<'\n';
    return 0;
}
 
 

Java代码：

import java.util.*;
import java.io.*;

class Pair {
	public double x;
	public double y;
	public Pair(double _x, double _y) {
		this.x = _x;
		this.y = _y;
	}
	
	@Override
	public boolean equals(Object obj) {
		if (this == obj) return true;
        if (obj == null || getClass() != obj.getClass()) return false;
		Pair p = (Pair)obj;
		return (p.x == x) && (p.y == y);
	}

	@Override
	public int hashCode() {
		return Objects.hash(x, y);
	}
	
}

public class Main {
	static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));

	
	public static void main(String[] args) throws Exception 
	{
		int n = Integer.parseInt(in.readLine().trim());
		double[] k = new double[n];
		double[] b = new double[n];
		String[] str;
		
		for(int i = 0;i < n;i++) {
			str = in.readLine().split(" ");
			k[i] = Double.parseDouble(str[0]);
			b[i] = Double.parseDouble(str[1]);
			
			for(int j = i - 1;j >= 0;j--) {
				if(k[i] == k[j] && b[i] == b[j]) {
					n--;
					i--;
					break;
				}
			}
		}
		
		
		Set<Pair> st = new HashSet<>();
		int ans = 2;
		for(int i = 1;i < n;i++) {
			for(int j = i - 1;j >= 0;j--) {
				if(k[i] == k[j]) continue;
				double x = (b[i] - b[j]) / (k[j] - k[i]);
				double y = k[i] * x + b[i];
				st.add(new Pair(x, y));
			}
			ans += st.size() + 1;
			st.clear();
		}
		
		System.out.println(ans);
	}
}