引言

这几道题是周赛里的几道题目，第一道题目我没用这种方法，但还是做出来了，用的一种比较特殊的思考方法，就是把每一个点都判断出来，不满足要求的就舍弃，因为 $n$ 很小，所以就过了。但第二道题就不一样了，还是要有正确的思路，这样一下子就出来了，就不用太多繁琐的细节判断了，不过慢慢积累，下次见到就会了，加油！

---

一、截断数组

标签：贪心

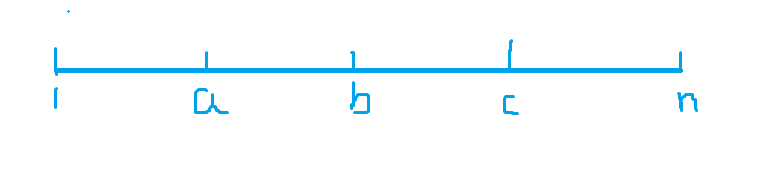
思路：如图所示，如果 $[1,a]$ 中的奇数和偶数的个数一样，那么 $(a,n]$ 中的奇数和偶数的个数也一样，如果 $[1,b]$ 中的奇数和偶数的个数一样，那么 $(a,b]$ 中的奇数和偶数个数也一样，如果 $[1,c]$ 中的奇数和偶数的个数相同，那么可得到划分的区间的奇数和偶数个数都一样。所以我们只要找到左半边奇数和偶数个数相同的点，那么这些点划分出来的区间都是满足要求的。还有一个条件就是截断成本不超过 $B$ ，那么我们只要把这些满足要求的点的花费放到一个集合里，再升序排列，直到超过 $B$ 为止，这时所截断操作的个数是最多的。

题目描述：

给定一个长度为 n 的整数数组 a1,a2,…,an。

如果一个整数数组恰好包含相同数量的奇数元素和偶数元素，就称该数组为一个平衡数组。

给定的数组 a 恰好就是一个平衡数组。

现在，我们可以将该数组从中间截断，从而得到若干个非空子数组。

关于截断操作：

每次操作都需要一定成本，具体来说，将数组从 ai 和 ai+1 之间截断，所需成本为 |ai−ai+1|。
所有进行的截断操作的总成本不得超过 B。
所有截断得到的子数组都必须也是平衡数组。
请你计算，在满足所有要求的前提下，最多可以进行多少次截断操作。

输入格式
第一行包含两个整数 n,B。

第二行包含 n 个整数 a1,a2,…,an。

输出格式
一个整数，表示在满足所有要求的前提下，可以进行的截断操作的最多次数。

数据范围
前 4 个测试点满足 2≤n≤6。
所有测试点满足 2≤n≤100，1≤B≤100，1≤ai≤100。

输入样例1：
6 4
1 2 5 10 15 20
输出样例1：
1
输入样例2：
4 10
1 3 2 4
输出样例2：
0
输入样例3：
6 100
1 2 3 4 5 6
输出样例3：
2

示例代码：

#include <bits/stdc++.h>

using namespace std;

const int N = 110;

int n, B;
int a[N], cost[N];

int main()
{
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    
    cin >> n >> B;
    for(int i = 1; i <= n; ++i) cin >> a[i];
    
    int odd = 0, even = 0, cnt = 0;
    for(int i = 1; i < n; ++i)
    {
        if(a[i] % 2) odd++;
        else even++;
        
        if(odd == even) cost[cnt++] = abs(a[i+1] - a[i]);
    }
    
    sort(cost, cost+cnt);
    
    int res = 0, sum = 0;
    for(int i = 0; i < cnt; ++i)
    {
        sum += cost[i];
        if(sum > B) break;
        res++;
    }
    
    cout << res << endl;
    return 0;
}

---

二、双端队列

标签：分类讨论、贪心

思路：就是分类讨论的一道题。我们用 $a$ 和 $b$ 来表示队头和队尾两个元素， $last$ 代表上一次取的元素。1. $a,b>last$，那么肯定是选小的取出来，不然另一头就永远不会动了。2. $a=b>last$，那么从一边取了之后，另一边是不会再取了，所以我们提前模拟看从哪一边取会取得更多就取哪边。3. $a|b>last$， 那么只能取大的一边了。4. $a,b<=last$ ，结束模拟。

题目描述：

给定一个长度为 n 的双端队列 a1,a2,…,an。

作为双端队列，我们既可以从队列的左端弹出元素，也可以从队列的右端弹出元素。

我们希望弹出尽可能多的元素，并要求所有弹出元素按照弹出顺序进行排列，刚好可以构成一个严格递增的序列。

请你计算，最多可以弹出多少个元素。

输入格式
第一行包含整数 n。

第二行包含 n 个整数 a1,a2,…,an。

输出格式
输出一个整数 k，表示最大弹出元素数量。

数据范围
前 6 个测试点满足 1≤n≤10。
所有测试点满足 1≤n≤2×105，1≤ai≤2×105。

输入样例1：
5
1 2 4 3 2
输出样例1：
4
输入样例2：
7
1 3 5 6 5 4 2
输出样例2：
6
输入样例3：
3
2 2 2
输出样例3：
1
输入样例4：
4
1 2 4 3
输出样例4：
4

示例代码：

#include <bits/stdc++.h>

using namespace std;

int n;
deque<int> q;

int main()
{
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    
    cin >> n;
    while(n--)
    {
        int t; cin >> t;
        q.push_back(t);
    }
    
    int res = 0, last = 0;
    while(q.size())
    {
        int a = q.front(), b = q.back();
        if(a > last && b > last)
        {
            res++;
            if(a < b) q.pop_front(), last = a;
            else if(b < a) q.pop_back(), last = b;
            else 
            {
                deque<int> backup(q);
                int t1 = 0, t2 = 0, t = last;
                while(q.size() && q.front() > last)
                {
                    t1++, last = q.front(), q.pop_front();
                }
                
                q = backup;
                last = t;
                while(q.size() && q.back() > last)
                {
                    t2++, last = q.back(), q.pop_back();
                }
                
                q = backup;
                if(t1 > t2) q.pop_front(), last = a;
                else q.pop_back(), last = b;
            }
        }
        else if(a > last)
        {
            res++;
            q.pop_front();
            last = a;
        }
        else if(b > last)
        {
            res++;
            q.pop_back();
            last = b;
        }
        else break;
    }
    
    cout << res << endl;
    
    return 0;
}

---

三、日期统计

标签：暴力枚举、日期问题

思路：就是暴力枚举，每个区间因为年是给定的，所以时间复杂度只有 $O(N^4)$ ，$N=100$ ，总的时间为 $10^8$ ，一秒就能跑出来，然后用 $set$ 来判重即可。

题目描述：

示例代码：

#include <bits/stdc++.h>

using namespace std;

const int N = 110;

int nums[N];
unordered_set<int> sset;

const int days[13] = {0,31,28,31,30,31,30,31,31,30,31,30,31};

bool is_leap(int y)
{
    if(y % 400 == 0 || y % 4 == 0 && y % 100 != 0) return true;
    return false;
}

int get_month_day(int y, int m)
{
    if(m == 2) return days[m] + is_leap(y);
    return days[m];
}

bool is_vaild(int y, int m, int d)
{
    if(m < 1 || m > 12 || d < 1 || d > 31) return false;
    return d <= get_month_day(y,m);
}

int main()
{
    for(int i = 0; i < 100; ++i) cin >> nums[i];

    int res = 0;
    for(int y1 = 0; y1 < 100; ++y1)
    {
        if(nums[y1] != 2) continue;
        for(int y2 = y1 + 1; y2 < 100; ++y2)
        {
            if(nums[y2] != 0) continue;
            for(int y3 = y2 + 1; y3 < 100; ++y3)
            {
                if(nums[y3] != 2) continue;
                for(int y4 = y3 + 1; y4 < 100; ++ y4)
                {
                    if(nums[y4] != 3) continue;

                    for(int m1 = y4 + 1; m1 < 100; ++m1)
                    {
                        for(int m2 = m1 + 1; m2 < 100; ++m2)
                        {
                            for(int d1 = m2 + 1; d1 < 100; ++d1)
                            {
                                for(int d2 = d1 + 1; d2 < 100; ++d2)
                                {
                                    int y = 2023, m = nums[m1] * 10 + nums[m2], d = nums[d1] * 10 + nums[d2];
                                    int date = y * 10000 + m * 100 + d;
                                    if(sset.count(date)) continue;
                                    sset.insert(date);
                                    if(is_vaild(y,m,d)) res++;
                                }
                            }
                        }
                    }
                }
            }
        }
    }

    cout << res << endl;
    return 0;
}