目录

一、场的概念

二、场的分类

三、数量场（标量场）的等值面

四、矢量场中的矢量线

矢量线方程推导：

---

一、场的概念

场在数学上是指一个向量到另一个向量或数的映射。场指物体在空间中的分布情况。场是用空间位置函数来表征的。在物理学中，经常要研究某种物理量在空间的分布和变化规律。

场https://baike.baidu.com/item/%E5%9C%BA/7451287

二、场的分类

1、数量场（标量场），矢量场；

2、稳定场（恒定场）【不随时间变化的场】，时变场；

三、数量场（标量场）的等值面

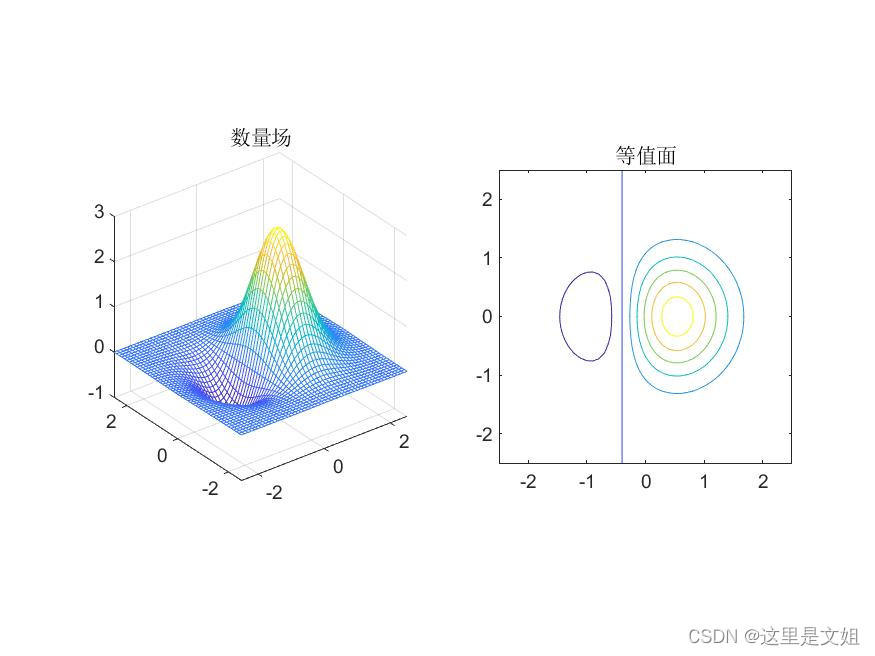
上图中左图是一个数量场的模型，右图是该数量场的等值面。数量场（标量场）是表示只有大小没有方向的场。

数量场（标量场）的数学表达式：

等值面的数学表达式：   ,    

任意常数；

空间中有无穷多个等值面。注意：任意两个等值面不可能相交。

在工程使用中我们通常会让。这样可以方便我们观察沿着不同方向 场的变化。

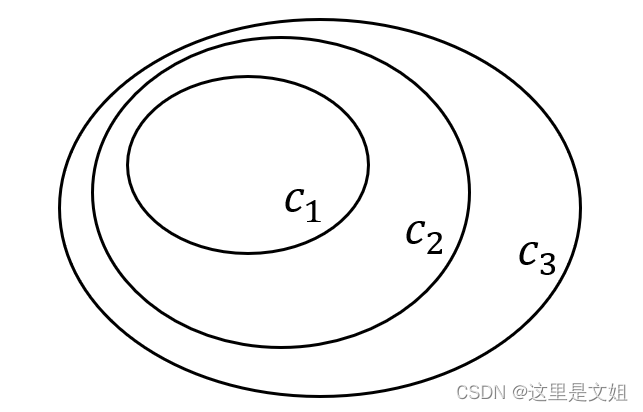
四、矢量场中的矢量线

矢量线数学表达式：

其中为x，y，z方向上的单位矢量。

矢量线是空间中一条有向曲线。其中每个点的方向是矢量线在该点的切线方向。矢量线反应了A的方向在空间中变化的情况。

无穷多根矢量线中，任意两根矢量线是不相交的。

矢量线方程推导：

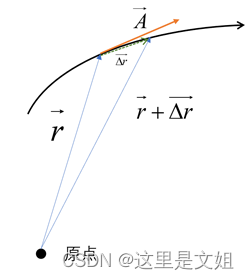
无穷小时，与平行，所以得出矢量线的方程:

矢量线方程式是微分方程，一个微分方程有无穷多个解

矢量场变化快的时候，矢量线密集，矢量场变化慢的时候，矢量线画的稀疏。

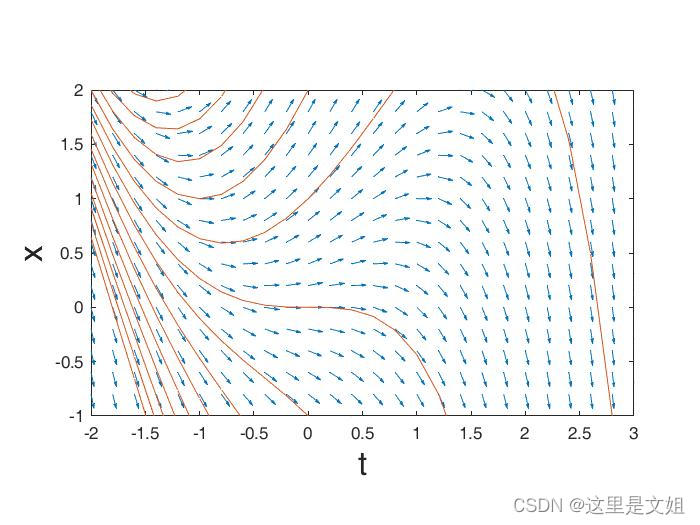
上面图片分别来源：MATLAB quiver函数使用：绘制矢量箭头-CSDN博客

matlab解微分方程：方向场_matble怎么画方向场-CSDN博客