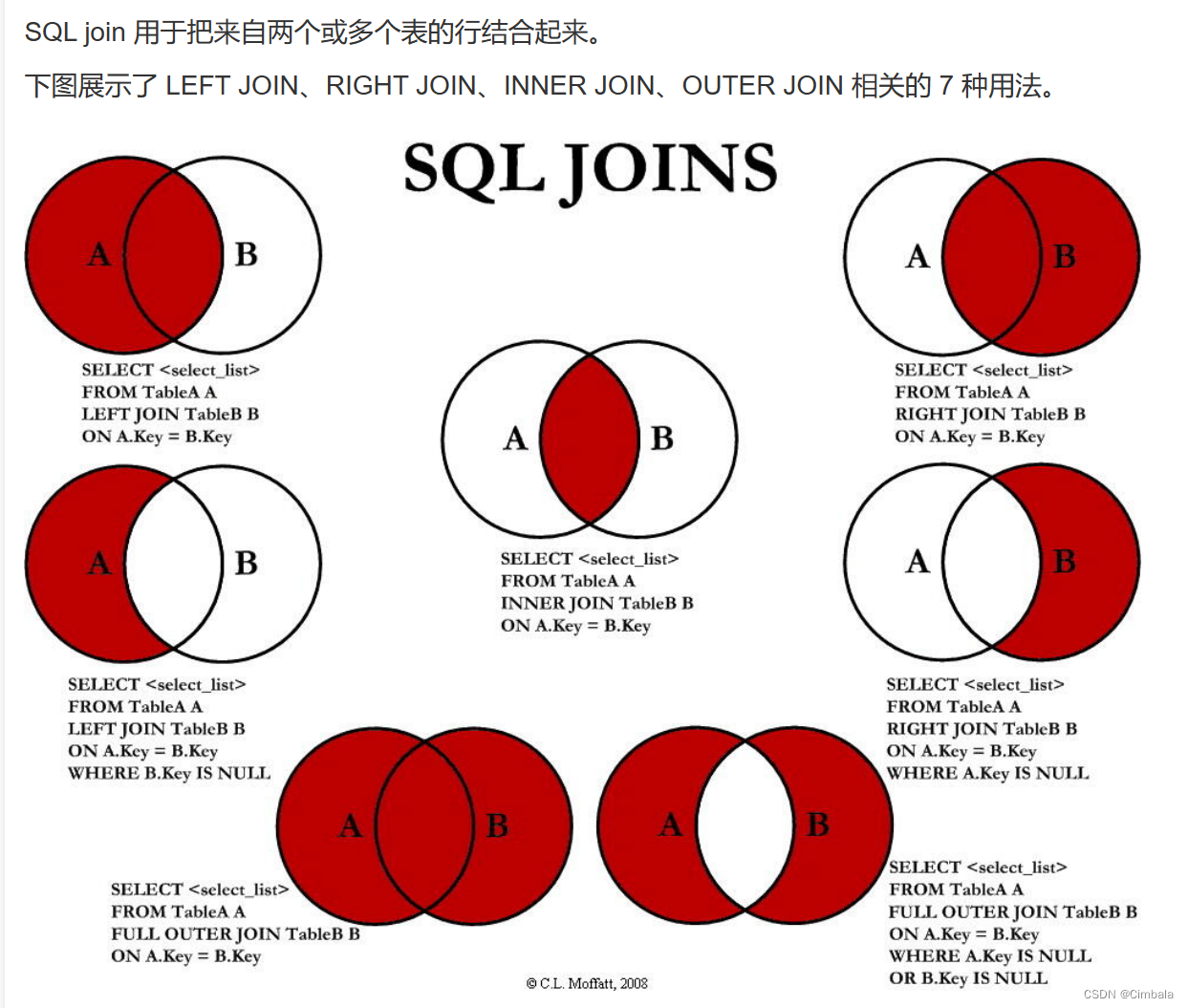
文章目录
- 1. 基本概念
- 1.1 基本术语
- 属性 (Attribute)
- 域 (Domain)
- 元数(Arity) / 目 (Cardinality)/ 度 (Degree)
- 元组
- 候选码 (Candidate Key)
- 主码 (Primary Key)
- 主属性 (Prime Attribute)
- 外码 (Foreign Key)
- 全码 (All-key)
- 笛卡尔积
- 1.2 关系数据库模式
- 关系模式
- 1.3 关系的完整性约束
- 实体完整性 (Entity Integrity)
- 2)参照完整性 (Referential Integrity)
- 3)用户定义完整性 (User Defined Integrity)
- 2. 关系运算
- 2.1 并 (Union )
- 2.2 差 (Difference)
- 2.3 广义笛卡尔积 (Extended Cartesian Product)
- 2.4 投影 (Projection)
- 2.5 选择 (Selection)
- 2.6 交 (Intersection)
- 2.7 连接 (Join)
- 2.7.1 θ连接
- 1)表示一
- 2)表示二
- 3)表示三
- 2.7.2 等值连接 (Equijoin)
- 2.7.3 自然连接 (Natural Join)
- 2.8 除 (Division)
- 2.9 广义投影 (Generalized Projection)
- 2.10 外连接 (Outer Jion)
- 1)左外连接
- 2)右外连接
- 3)全外连接
- 2.11 聚集函数
- 3. 关系数据库设计基本理论
1. 基本概念
1.1 基本术语
属性 (Attribute)
- 概念:在现实世界中,要描述一个事物常常取若干特征来表示,这些特征称为属性
- 如:学生通过学号、姓名、性别、系别、年龄、籍贯等属性来描述
域 (Domain)
- 概念:每个属性的取值范围对应一个值的集合,称为该属性的域
如:学号的域是6位整型数;姓名的域是10位字符;性别的域为{男,女}等
- 第一范式对域的限制:所有的域都应是原子数据 (Atomic Data)
- 原子数据如:整数、字符串
- 非原子数据:集合、记录、数组
元数(Arity) / 目 (Cardinality)/ 度 (Degree)
指的是关系模型中属性的个数(即表中列的个数)
元组
即,一组元,也就是表中的一行。
候选码 (Candidate Key)
若关系中的某一属性或属性组的值能唯一的标识一个元组,则称该属性或属性组为候选码。
主码 (Primary Key)
- 即主键
- 若一个关系有多个候选码,则选定其中一个作为主码。
主属性 (Prime Attribute)
- 主属性:包含在任何候选码中的属性
- 非主属性(Non-Prime Attribute):不包含在任何候选码中的属性
外码 (Foreign Key)
如果关系模式 R 中的属性或属性组不是该关系的码,但它是其他关系的码,那么该属性集对关系模式R 而言是外码。
举例:
客户与贷款之间的借贷联系 c-1(c-id,loan-no)
属性c-id是客户关系中的码,所以c-id 是外码
属性 loan-no是贷款关系中的码,所以loan-no 也是外码。
全码 (All-key)
关系模型的所有属性组是这个关系模式的候选码,称为全码。
示例:
关系模式R(T,C,S), 属性 T 表示教师,属性C 表示课程,属性S 表示学生。
假设一个教师可以讲授多门课程,某门课程可以由多个教师讲授,学生可以听不同教师讲授的不同课程,那么,要想区分关系中的每一个元组,这个关系模式R 的码应为全属性 T、C和 S,即ALL-KEY。
笛卡尔积
- 设D1,D2,D3,…,Dn为任意集合
- 定义D1,D2,D3,…,Dn的笛卡尔积为:D1×D2×D3×…×Dn={(d1,d2,d3…,dn)|di∈Di,i=1,2,3,…,n}
- 集合中的每一个元素(d1,d2,d3…,dn)叫作一个n 元 组,元素中的每一个值di 叫作元组一个分量
- 若Di=(i=1,2,3,…,n) 为有限集,其基数(Cardinal Number, 元组的个数)为 mi(i=1,2,3,…,n), 则 D1,D2,D3,…,Dn, 的基数M为:

1.2 关系数据库模式
模式:关系行数据库的型,是关系数据库结构的描述
- 包括:若干域的定义、以及在这些域上定义的若干关系模式
- 值
- 这些关系模式在某一时刻对应的关系的集合
在数据库中要区分型和值。关系数据库中的型也称为关系数据库模式,是关系数据库结构的描述。
- 这些关系模式在某一时刻对应的关系的集合
关系模式
-
关系模式 (Relation Schema):是关系的描述
-
可以形式化地表示为:R(U,D,dom,F)
- R 表示关系名
- U 是组成该关系的属性名集合
- D 是属性的域
- dom是属性向域的映像集合
- F 为属性间数据的依赖关系集合。
-
通常将关系模式简记为:R(U) 或R(A1,A2,A3,…,An)
- R 为关系名
- A1,A2,A3,…,An为属性名或域名
属性向域的映像常常直接说明属性的类型、长度通常在关系模式主属性上加下画线表示该属性为主码属性。
-
举例:
- 学生关系S 有学号Sno、 学生姓名 Same、 系名 SD、 年龄S A属性
- 课程关系 C 有课程号Cno、 课程名Cname、 先修课程号PCno属性
- 学生选课关系 SC有学号 Sno、 课程号Cno、 成绩Grade属性
- 定义关系模式及主码如下(本题未考虑F 属性间数据的依赖,该问题在后续内容讨论)。
- 学生关系模式S(Sno,Sname,SD,SA)。
- 课程关系模式C(Cno,Cname,PCno),Dom(PCno)=Cno。
- PCno 是先行课程号,来自 Cno域,但由于 PCno属性名不等于Cno值域名,所以要用 Dom来定义。但是,不
能将Pcno直接改为Cno, 因为在关系模型中,各列属性必须取相异的名字。
(3)学生选课关系模式SC(Sno,Cno,Grade)。SC关系中的Sno、Cno又分别为外码。
因为它们分别是S、C关系中的主码。
- PCno 是先行课程号,来自 Cno域,但由于 PCno属性名不等于Cno值域名,所以要用 Dom来定义。但是,不
1.3 关系的完整性约束
-
作用:防止对数据的意外破坏
完整性规则提供了一种手段来保证当授权用户对数据库做修改时不会破坏数据的一致性。
-
举例
某企业实验室管理员的基本薪资小于2000元,则可用完整性规则来进行约束。 -
关系的完整性约束共分为3类:
实体完整性 (Entity Integrity)
- 要求每个数据表:
- 必须有主键
- 主键的所有字段,其属性必须是唯一且非空值。
2)参照完整性 (Referential Integrity)
- 参照完整性规定
- 若 F 是基本关系 R 的外码,它与基本关系S 的主码Ks相对应
- 则对于R 中每个元组在F上的值或者取空值或者等于S 中某个元组的主码值
简单的说,外码要么是空,要么是对应表中某个主码的值
举例:
某企业员工Emp 关系模式和部门 Dept关系模式表示如下:Emp (员工号,姓名,性别,参加工作时间,部门号)Dept (部门号,名称,电话,负责人)Emp和Dept关系存在着属性的引用,即员工关系中的“部门号”值必须是确实存在的部门的部门号。按照关系的完整性规则,员工关系中的“部门号”属性取值要参照部门关系的“部门号”属性取值。如果新入职的员工还未分配具体的部门,那么部门号取空值。
- 表示:
- 主码属性:加实下划线
- 外码属性:加虚下划线
3)用户定义完整性 (User Defined Integrity)
- 概述:
- 针对某一具体的关系数据库的约束条件
- 反映某一具体应用所涉及的数据必须满足的语义要求,由应用的环境决定
例如,银行的用户账户规定必须大于等于100000,小于999999。
2. 关系运算
替换下边这张图
- 关系操作的特点:操作对象和操作结果都是集合。
- 关系代数运算符分类
- 集合运算符:并(∪)、交(∩)、差(-)、笛卡尔积(×)
- 专门的关系运算符:选择(σ)、投影(π)、连接(∞)、除(÷)
- 算术比较符:>、≥、<、≤、=、≠
- 逻辑运算符:非(¬),与(∧)、或(∨)、
2.1 并 (Union )
-
先决条件:关系R 与S 具有相同的关系模式
即R 与S 的元数相同(结构相同)
-
关系R 与 S 的并:由属于R 或属于S 的元组构成的集合组成,记作RUS
-
其形式定义: RUS={t | t ∈ R∨t∈S}
- t 为元组变量
- ∈属于,∉ 不属于
2.2 差 (Difference)
- 先决条件:关系 R 与 S具有相同的关系模式
- 关系R 与 S 的差:由属于 R 但不属于S 的元组构成的集合,记作R-S
- 其形式定义:R-S={t|t∈R∧t ∉ S}
2.3 广义笛卡尔积 (Extended Cartesian Product)
- 条件:关系R有n目,关系S有m目
- 广义笛卡尔积:
- 概述:是一个 (n+m) 列的元组的集合,元组的
- 前 n 列是关系R 的一个元组
- 后m 列是关系S 的一个元组
- 记作:R×S
- 概述:是一个 (n+m) 列的元组的集合,元组的
- 形式定义如下:R×S={t | t=<tn,tm > ∧ tn∈ R ∧ tm∈ S}
- t=<tn,tm> :元组t由两个元素组成,分别是tn和tm
- tn∈ R:tn是关系R中的一个元素
- tm∈ S:tm是关系S中的一个元素
- 如果R 和S 中有相同的属性名,可在属性名前加关系名作为限定,以示区别
- 若R 有K1 个元组,S 有K2个元组,则R 和S的广义笛卡尔积有K1×K2个元组
注意:本书中的<tn,tm>意为元组tn和tm拼接成的一个元组
2.4 投影 (Projection)
- 概述:
- 垂直方向进行运算
- 在关系R中选择出若干属性列A 组成新的关系
- 记作:πA( R)
- 其形式定义:πA( R)={t[A]|t∈R}
2.5 选择 (Selection)
- 概述:
- 水平方向进行运算
- 是从关系 R 中选择满足给定条件的诸元组
- 记作:σF( R)
- 其形式定义如下:σF( R)={t|t∈R∧F(t)= True}
- F 中的运算对象是属性名或常数,由运算符、算术比较符和逻辑运算符构成
示例:σ1≥6( R)表示选取R 关系中第1个属
性值大于等于第6个属性值的元组;σ1>6( R)表示选取R 关系中第1个属性值大于等于6的
元组。
扩展的关系运算可以从基本的关系运算中导出,主要包括:选择、投影、连接、除法、广
义笛卡尔积、外连接。
2.6 交 (Intersection)
- 概述:
- 条件:关系 R 与S 具有相同的关系模式
- 关系 R 与S 的交是由属于 R 同时又属于S 的元组构成的集合
- 记作:R∩S
- 其形式定义如下:R∩S={t|t∈R∧t∈S}
即: R∩S=R-(R-S) 或者 R∩S=S-(S-R)。
2.7 连接 (Join)
2.7.1 θ连接
- 概述:是从R 与S 的笛卡尔积中选取属性满足一定条件的元组
1)表示一
其形式定义如下:
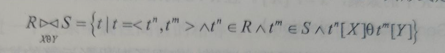
说明:
- ‘XθY’:连接的条件
- θ是比较运算符
- X 和 Y 分别为R 和 S 上度数相等,且可比的属性组
- tn [X] 表示R 中tn元组的相应于属性X 的一个分量
- tm [Y]表示S 中tm元组的相应于属性Y 的一个分量
{t|t=<tn,tm>∧ tn ∈R ∧ tm ∈S ∧tn [X]θ tm [Y] }
2)表示二
θ连接也可以表示为:
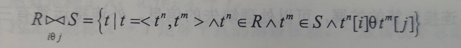
- 说明:
- i=1,2,3,…,n
- j=1,2,3,…,m
- ‘iθj’:从两个关系 R 和S 中选取R 的第i列 和 S 的第j 列之间满足θ运算的元组进行连接
3)表示三
θ连接可以由基本的关系运算笛卡尔积和选取运算导出,因此θ连接可表示为:
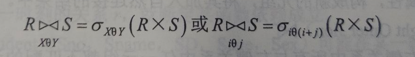
2.7.2 等值连接 (Equijoin)
-
概述:当θ为“=”时,称为等值连接
-
记为:
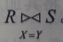
-
其形式定义如下:
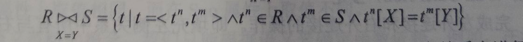
2.7.3 自然连接 (Natural Join)
-
概述:
- 是一种特殊的等值连接
- 要求两个关系中进行比较的分量必须是相同的属性组
- 并且在结果集中将重复属性列去掉。
- 记作:R∞S
-
其形式定义如下:

说明:
- tn 表示 R 关系的元组变量
- tm表示S 关系的元组变量
- R 和 S 具有相同的属性组B,且B=(B1,B2,…,Bx)
- 并假定 R 关系的属性为A1,A2,…,An-k,B1,B2,…,Bk
- S关系的属性为 B1,B2,…,Bk,Bk+1,Bk+2,…,Bm
- 为 S 的元组变量 tm去掉重复属性B 所组成的新的元组变量为tm’
-
自然连接可以由基本的关系运算笛卡尔积和选取运算导出,因此自然连接可表示为:

特别需要说明的是:一般连接是从关系的水平方向运算,而自然连接不仅要从关系的水平方向,而且也要从关系的垂直方向运算。因为自然连接要去掉重复属性,如果没有重复属性,那么自然连接就转化为笛卡儿积。
这一段整理出来
2.8 除 (Division)
- 概述
- 同时从水平方向和垂直方向运算
- 其形式定义:R÷S={tn [X]|tn∈R∧πy(S)⊆Yx}
- 条件:给定关系 R(X,Y) 和 S(Y,Z),X、Y、Z为属性组
- R÷S应当满足元组在X上的分量值x的象集Y,包含关系S 在属性组Y上投影的集合。
- Y,为x在R 中的象集,x=tn[X]。 且R÷S的结果集的属性组为X。
2.9 广义投影 (Generalized Projection)
- 概述:广义投影运算允许在投影列表中使用算术运算,实现了对投影运算的扩充。
- 若有关系R, 条件F1,F2,…,Fn中的每一个都是涉及R 中常量和属性的算术表达式,那么广义投影运算的形式定义为:πF1,F2,…,Fn(R )。
2.10 外连接 (Outer Jion)
- 概述:外连接运算是连接运算的扩展,可以处理缺失的信息
- 外连接运算有三种:
1)左外连接
- Left Outer Jion
- 符号:⋊
- 概念:取出左侧关系中所有与右侧关系中任一元组都不匹配的元组,用空值null充填所有来自右侧关系的属性,构成新的元组,将其加入自然连接的结果中。
2)右外连接
- Right Outer Jion
- 符号:⋉
- 概念:取出右侧关系中所有与左侧关系中任一元组都不匹配的元组,用空值null填充所有来自左侧关系的属性,构成新的元组,将其加入自然连接的结果中。
3)全外连接
- Full Outer Jion
- 符号:⋈
- 概念:完成左外连接和右外连接的操作
2.11 聚集函数
- 概念:聚集函数输入一个值的集合,返回单一值作为结果
例如,集合{2,4,6,8,10,15}。将聚集函数 sum用于该集合时返回和45
- 多重集合:结合中一个值可以出现多次(顺序无关紧要)
有时在计算聚集函数前必须去掉重复值,此时可以将 distinct用连接符附加在函数名后,如count-distinct。
3. 关系数据库设计基本理论
- 设计的目标:生成一组合适的、性能良好的关系模式,以减少系统中信息存储的冗余度,但又可以方便地获
取信息。
3.1 函数依赖
3.1.1 数据依赖
- 数据依赖:
- 是通过一个关系中属性间值的相等与否体现出来的数据间的相互关系
- 是现实世界属性间联系和约束的抽象,是数据内在的性质,是语义的体现
- 函数依赖是一种最重要、最基本的数据依赖
3.1.2 函数依赖
- 概念
- 条件:
- 设R(U) 是属性集 U上的关系模式, X、Y是 U的子集
- 若对 R(U) 的
任何一个可能的关系r,r中不可能存在两个元组 在X 上的属性值相等,而在Y 上的属性值不等人话:在X上相等,在Y上也相等。比如
供应商名 -> 所在地区
- 结论:则称X 函数决定 Y ,或 Y 函数依赖于X
- 记作:X→Y
- 条件:
- 注意
- 条件中关系r是任何可能关系,而不是某一时刻的关系。
- 如:某一时刻,r中的学生年龄都不同,我们并不能得出 “年龄 -> 学号”
- 函数依赖是语义范畴的概念,我们只能根据语义来确定函数依赖
如:在没有同名的情况下 “姓名 -> 年龄”,但有同名时则不成立
3.1.3 非平凡函数
- 概念
- 如果X→Y, 但 Y ⊊ X Y\subsetneq X Y⊊X
- 则称X→Y是非平凡的函数依赖
一般情况下总是讨论非平凡的函数依赖。
3.1.4 平凡依赖
- 概念:
- 如果 X → Y X \rightarrow Y X→Y , 但 Y ⊆ X Y\subseteq X Y⊆X
- 则称X→Y是平凡的函数依赖
3.1.5 完全函数依赖
- 概念
- R(U) 中,如果 X → Y X \rightarrow Y X→Y
- 对于X的任何一个真子集X′, 都有X’ 不能决定Y
- 则称 Y对X完全函数依赖
- 记作:X→Y
- 举例:
- 一个选课关系 SC(学号,课程号,成绩)
- 得到 F= {(学号,课程号)→ 成绩 }
- (学号,课程号)中的任何一个真子集“学号”或“课程号”都不能决定“成绩”
- 即,“成绩”完全依赖于(学号,课程号)
3.1.6 部分函数依赖
- 概念:
- 也称作局部函数依赖
- 如果X→Y, 但 Y 不完全函数依赖于X,
- 记作: X − − > p Y X\stackrel{p}{-\!-\!>}Y X−−>pY
3.1.7 传递依赖
- 概念:在R(U,F) 中,如果X→Y, Y ⊈ X Y\nsubseteq X Y⊈X, Y ↛ X Y\nrightarrow X Y↛X ,Y→Z, 则称Z对X传递依赖。
3.2 多值依赖
1)概念
- 条件:
- 关系模式R(U) 中,X Y Z是 U的子集,Z=U-X-Y
- 当且仅当对 R(U)的任何一个关系 r, 给定一对(x, z) 值,有一组 Y 的值,这组值只由x值决定而与 z 值无关,
- 则称 “Y多值依赖于X”或 “X多值决定 Y”成立。
- 记为: X→→Y。
2)多值依赖性质
多值依赖具有以下6条性质:
- 对称性
即若X→→Y,则X→→Z,其中Z=U-X-Y
- 传递性
即若X→→Y,Y→→Z,则X→→Z-Y。
- 函数依赖可以看成是多值依赖的特殊情况
- 若X→→Y,X→→Z, 则X→→YZ
- 若X→→Y,X→→Z, 则X→→Y∩Z
- 若X→→Y,X→→Z, 则X→→Z-Y
3.3 规范化
- 作用:评价模式规范化的程度
- 包括: INF、2NF、3NF、BCNF、4NF、5NF
- 规范化:通过分解,将一个低一级范式的关系模式转换成若干个高一级范式的关系模式,
3.3.1 1NF(第一范式)
1)概述
- 定义:若关系模式R 的每一个分量都是不可再分的数据项,则关系模式R 属于第一范式。
- 记为:R∈1NF。
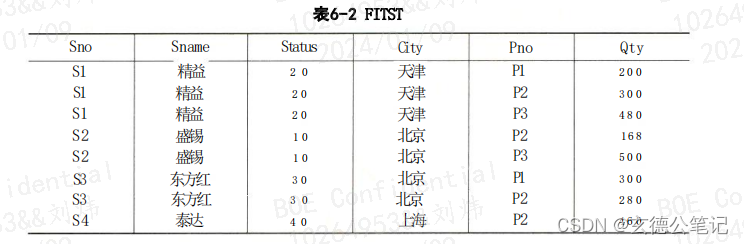
示例:以供应者和它所提供的零件信息为例
- 关系模式:FIRST(Sno,Sname,Status,City,Pno,Qty)
- 函数依赖关系:F={Sno → Sname,Sno → Status,Status → City,(Sno,Pno)→ Qty}
如上可见,每一个分量都是不可再分的了。
2)存在问题
- 冗余度大
如:每个供应者的 Sno、Sname、Status、City反复存储。
- 引起修改操作的不一致性
如:供应者S1 从“天津”搬到“上海”,需要修改每一条数据,否则导致数据修改的不一致性。
- 插入异常
如:主码为Sno、Pno,若供应商未给出Pno则插入异常
- 删除异常
如:供应商 S4 的P2 零件销售完了,并且以后不再销售P 2零件,那么应删除该元组。则表中S4的信息将没有保留。
3.3.2 2NF(第二范式)
1)要求
- 满足1NF
- 每一个非主属性完全依赖于码
2)举例
- 上例不是2NF的原因
- FIRST关系中的码是Sno、Pno
- Status仅依赖于Sno,而不依赖于Pno
- 因此非主属性 Status部分函数依赖于码,故非2N F
- 改造:
- 将FIRST关系分解:
- FIRST1(Sno,Sname,Status,City)
- FIRST2 (Sno,Pno,Qty)
- 符合2NF:两个关系的所有非主属性都依赖于各自的码
- F={Sno → Sname, Sno → Status, Status → City}
- F={(Sno,Pno)→ Qty}
- 将FIRST关系分解:
3.3.3 3NF(第三范式)
1)要求
- 符合2NF
- 消除除了非主属性对码的传递函数依赖
2)举例
- 上例中 FIRS1≠3NF
- F={Sno → Status,Status → City},存在传递依赖
- 改造:
- 将FIRS1分解
- FIRS11(Sno,Sname,Status)
- FIRS12(Status,City)
- 符合第三范式:消除了传递依赖
- F={Sno → Sname, Sno → Status}
- F={Status → City}
- 将FIRS1分解
3.3.4 BCNF(巴克斯范式)
- BCNF(Boyce Codd Normal Form),
【定义6.10】关系模式R∈INF, 若X→Y且Y∈X时,X 必含有码,则关系模式R∈BCNF。
也就是说,当,则称为BCNF。
1)要求
- 满足3NF
- 消除了
主属性对码的部分函数依赖和传递函数依赖
注意:3NF消除的传递依赖是非主属性的。
2)举例
- 条件
- R(Pno,Pname,Mname) 的属性分别表示零件号、零件名、厂商名
- 每种零件号只有一个零件名,但不同的零件号可以有相同的零件名
- 每种零件可以有多个厂商生产,但每家厂商生产的零件零件名不同
- 符合3NF
- 获得函数依赖:
- Pno → Pname
- (Pname,Mname)→ Pno
- 符合3NF:
- 推知R中候选码为 (Pname,Mname) 或 (Pno,Mname)
- 所以所有属性都是主属性
- 说以不存在非主属性依赖,即符合3NF
- 获得函数依赖:
- 不符合BCNF
- 主属性Pname传递依赖于码 (Pname,Mname)。
BCNF消除了主属性的传递依赖
- 主属性Pname传递依赖于码 (Pname,Mname)。
- 改造
- 分解:R1(Pno,Pname) 和 R2(Pno,Mname)
3.3.4 4NF(第四范式)
- 满足条件
- 1NF
- 属性间不允许有非平凡且非函数依赖的多值依赖
- 示例
- 关系模式R∈lNF
- 若对于 R 的每个非平凡多值依赖X→→Y
- 且 Y ⊈ X Y\nsubseteq X Y⊈X
- X必含有码
- 则关系模式R(U,F) ∈ \in ∈ 4NF。
只考虑函数依赖,关系模式最高的规范化程度是BCNF
考虑多值依赖,关系模式最高的规范化程度是4NF