向量基础
- 1、向量和线性组合
- 2、向量的模和点乘
- 3、矩阵
- 4、参考
线性代数的核心是向量的加和乘两种运算的组合,本篇博客为线性代数的一个引子,主要从向量、线性组合和矩阵逐步引出线性代数的相关知识。
1、向量和线性组合
首先介绍的是向量相关,向量是基础。
已知列向量:
υ
=
[
v
1
v
2
]
\boldsymbol{\upsilon}=\left[\begin{matrix} v_1 \\ v_2\end{matrix} \right]
υ=[v1v2],
ω
=
[
w
1
w
2
]
\boldsymbol{\omega}=\left[\begin{matrix} w_1 \\ w_2\end{matrix} \right]
ω=[w1w2];
向量加法: υ + ω = [ v 1 + w 1 v 2 + w 2 ] \boldsymbol{\upsilon}+\boldsymbol{\omega}=\left[\begin{matrix} v_1+w_1 \\ v_2+w_2\end{matrix} \right] υ+ω=[v1+w1v2+w2];
纯量乘法: c υ = [ c v 1 c v 2 ] c\boldsymbol{\upsilon}=\left[\begin{matrix} cv_1 \\ cv_2\end{matrix} \right] cυ=[cv1cv2], c c c是标量;
线性组合:我们将
υ
\boldsymbol{\upsilon}
υ和
ω
\boldsymbol{\omega}
ω的加法运算和标量乘法运算结合起来,得到的结果称为
υ
\boldsymbol{\upsilon}
υ和
ω
\boldsymbol{\omega}
ω的线性组合,即
c
υ
+
d
ω
c\boldsymbol{\upsilon}+d\boldsymbol{\omega}
cυ+dω。
两个向量的线性组合就是线性代数的最简单的形式。
下图展示了向量加法的结果:

Tip:列向量
υ
=
[
a
b
c
]
\boldsymbol{\upsilon}=\left[\begin{matrix} a \\ b \\ c\end{matrix} \right]
υ=⎣⎡abc⎦⎤也可以写为
υ
=
(
a
,
b
,
c
)
\boldsymbol{\upsilon}=( a , b , c )
υ=(a,b,c),这两种形式都是表示列向量,后一种可以节约书写空间。另外,行向量表示为
υ
=
[
a
,
b
,
c
]
\boldsymbol{\upsilon}=[ a , b , c ]
υ=[a,b,c],平躺着并用方括号表示。
2、向量的模和点乘
点乘(内积):点乘为两个向量对应位置上元素乘积的和。
向量
υ
=
(
v
1
,
v
2
,
v
3
,
.
.
.
,
v
n
)
\boldsymbol{\upsilon}=( v_1 , v_2 , v_3,...,v_n )
υ=(v1,v2,v3,...,vn)和向量
ω
=
(
w
1
,
w
2
,
w
3
,
.
.
.
,
w
n
)
\boldsymbol{\omega}=( w_1 , w_2 , w_3,...,w_n )
ω=(w1,w2,w3,...,wn)的点乘表示为:
υ
⋅
ω
=
v
1
w
1
+
v
2
w
2
+
.
.
.
+
v
n
w
n
\boldsymbol{\upsilon} \cdot \boldsymbol{\omega}=v_1w_1+v_2w_2+...+v_nw_n
υ⋅ω=v1w1+v2w2+...+vnwn
向量
υ
=
(
v
1
,
v
2
,
v
3
,
.
.
.
,
v
n
)
\boldsymbol{\upsilon}=( v_1 , v_2 , v_3,...,v_n )
υ=(v1,v2,v3,...,vn)和其自身的点乘为:
υ
⋅
υ
=
v
1
2
+
v
2
2
+
.
.
.
+
v
n
2
=
(
v
1
−
0
)
2
+
(
v
2
−
0
)
2
+
.
.
.
+
(
v
n
−
0
)
2
\boldsymbol{\upsilon} \cdot \boldsymbol{\upsilon}=v^2_1+v^2_2+...+v^2_n=(v_1-0)^2+(v_2-0)^2+...+(v_n-0)^2
υ⋅υ=v12+v22+...+vn2=(v1−0)2+(v2−0)2+...+(vn−0)2
向量的长度(模)
则在
n
n
n维坐标系中,
υ
⋅
υ
\boldsymbol{\upsilon} \cdot \boldsymbol{\upsilon}
υ⋅υ表示点
(
v
1
,
v
2
,
v
3
,
.
.
.
,
v
n
)
( v_1 , v_2 , v_3,...,v_n)
(v1,v2,v3,...,vn)到坐标原点的距离的平方,即向量
υ
\boldsymbol{\upsilon}
υ的长度的平方,所以向量
υ
\boldsymbol{\upsilon}
υ的长度为:
l
e
n
g
t
h
=
∥
υ
∥
=
υ
⋅
υ
=
(
v
1
2
+
v
2
2
+
.
.
.
+
v
n
2
)
1
/
2
\mathbf{length}= \left \|\boldsymbol{\upsilon}\right\|=\sqrt{\boldsymbol{\upsilon} \cdot \boldsymbol{\upsilon}}=(v^2_1+v^2_2+...+v^2_n)^{1/2}
length=∥υ∥=υ⋅υ=(v12+v22+...+vn2)1/2
如下图所示:

单位向量
单位向量是长度等于1的向量,则向量
υ
\boldsymbol{\upsilon}
υ的单位向量
u
\boldsymbol{u}
u为任何非零向量除以该向量的长度,即:
u
=
υ
∥
υ
∥
\boldsymbol{u}=\frac{\boldsymbol{\upsilon}}{ \left \|\boldsymbol{\upsilon}\right\|}
u=∥υ∥υ
下图为单位向量的示意图:

对于非零向量,当向量
υ
\boldsymbol{\upsilon}
υ垂直向量
ω
\boldsymbol{\omega}
ω时,它们的点积为零,即:
υ
⋅
ω
=
0
\boldsymbol{\upsilon} \cdot \boldsymbol{\omega}=0
υ⋅ω=0
可结合勾股定理进行证明。
向量夹角
设向量
υ
\boldsymbol{\upsilon}
υ和向量
ω
\boldsymbol{\omega}
ω的夹角为
θ
\theta
θ,当
υ
⋅
ω
!
=
0
\boldsymbol{\upsilon} \cdot \boldsymbol{\omega}!=0
υ⋅ω!=0时,会有:
{
θ
<
9
0
∘
,
υ
⋅
ω
>
0
θ
>
9
0
∘
,
υ
⋅
ω
<
0
\left\{\begin{array}{cc} \theta<90^{\circ}, & \boldsymbol{\upsilon} \cdot \boldsymbol{\omega}>0\\ \theta>90^{\circ}, & \boldsymbol{\upsilon} \cdot \boldsymbol{\omega}<0 \end{array}\right.
{θ<90∘,θ>90∘,υ⋅ω>0υ⋅ω<0
除此之外,两个单位向量的点乘也表示两个向量夹角
θ
\theta
θ的
c
o
s
i
n
e
cosine
cosine余弦值:
u
⋅
U
=
c
o
s
θ
,
u
⋅
U
≤
1
\boldsymbol{u} \cdot \boldsymbol{U}=cos{\theta},\boldsymbol{u} \cdot \boldsymbol{U}\leq1
u⋅U=cosθ,u⋅U≤1

那么对于非单位向量的向量
υ
\boldsymbol{\upsilon}
υ和向量
ω
\boldsymbol{\omega}
ω的夹角的余弦值应该怎么表示?
综上所述,应该为这两个向量对应的单位向量的点乘,即:
c
o
s
θ
=
(
υ
∥
υ
∥
)
⋅
(
ω
∥
ω
∥
)
=
υ
⋅
ω
∥
υ
∥
∥
ω
∥
≤
1
cos\theta = (\frac{\boldsymbol{\upsilon}}{\left \|\boldsymbol{\upsilon}\right\|}) \cdot (\frac{\boldsymbol{\omega}}{\left \|\boldsymbol{\omega}\right\|})=\frac{\boldsymbol{\upsilon} \cdot \boldsymbol{\omega}}{\left \|\boldsymbol{\upsilon}\right\|\left \|\boldsymbol{\omega}\right\|}\leq1
cosθ=(∥υ∥υ)⋅(∥ω∥ω)=∥υ∥∥ω∥υ⋅ω≤1
由此可引出两个著名的不等式:
柯西-施瓦兹-布尼亚科夫斯基不等式 ∣ υ ⋅ ω ∣ ≤ ∥ υ ∥ ∥ ω ∥ | \boldsymbol{\upsilon} \cdot \boldsymbol{\omega}|\leq{\left \|\boldsymbol{\upsilon}\right\|\left \|\boldsymbol{\omega}\right\|} ∣υ⋅ω∣≤∥υ∥∥ω∥
三角不等式: ∥ υ + ω ∥ ≤ ∥ υ ∥ + ∥ ω ∥ {\left \|\boldsymbol{\upsilon}+\boldsymbol{\omega}\right\|}\leq{\left \|\boldsymbol{\upsilon}\right\|+\left \|\boldsymbol{\omega}\right\|} ∥υ+ω∥≤∥υ∥+∥ω∥
3、矩阵
接下来,我们从向量过度到矩阵,用矩阵表示线性组合。前面介绍了向量之间的运算,那么当一个矩阵乘以一个向量应如何去理解呢?
首先给定三个向量:
u
=
[
1
−
1
0
]
,
υ
=
[
0
1
−
1
]
,
ω
=
[
0
0
1
]
.
\boldsymbol{u}=\left[\begin{matrix} 1 \\ -1 \\ 0\end{matrix} \right],\boldsymbol{\upsilon}=\left[\begin{matrix} 0 \\ 1 \\ -1\end{matrix} \right],\boldsymbol{\omega}=\left[\begin{matrix} 0 \\ 0 \\ 1\end{matrix} \right].
u=⎣⎡1−10⎦⎤,υ=⎣⎡01−1⎦⎤,ω=⎣⎡001⎦⎤.
则这三个三维向量的线性组合为:
x
1
u
+
x
2
υ
+
x
3
ω
x_1\boldsymbol{u}+x_2\boldsymbol{\upsilon}+x_3\boldsymbol{\omega}
x1u+x2υ+x3ω,即:
x
1
[
1
−
1
0
]
+
x
2
[
0
1
−
1
]
+
x
3
[
0
0
1
]
=
[
x
1
x
2
−
x
1
x
3
−
x
2
]
x_1\left[\begin{matrix} 1 \\ -1 \\ 0\end{matrix} \right]+x_2\left[\begin{matrix} 0 \\ 1 \\ -1\end{matrix} \right]+x_3\left[\begin{matrix} 0 \\ 0 \\ 1\end{matrix} \right]=\left[\begin{matrix} x_1 \\ x_2-x_1 \\ x_3-x_2\end{matrix} \right]
x1⎣⎡1−10⎦⎤+x2⎣⎡01−1⎦⎤+x3⎣⎡001⎦⎤=⎣⎡x1x2−x1x3−x2⎦⎤
那么用矩阵重写上面的线性组合为:
A
x
=
[
1
0
0
−
1
1
0
0
−
1
1
]
[
x
1
x
2
x
3
]
=
[
x
1
x
2
−
x
1
x
3
−
x
2
]
=
[
b
1
b
2
b
3
]
=
b
A\boldsymbol{x}=\left[\begin{matrix} 1 & 0 & 0\\ -1 & 1 & 0\\ 0 & -1 & 1\end{matrix} \right]\left[\begin{matrix} x_1 \\ x_2 \\ x_3\end{matrix} \right]=\left[\begin{matrix} x_1 \\ x_2-x_1 \\ x_3-x_2\end{matrix} \right]=\left[\begin{matrix} b_1 \\ b_2 \\ b_3\end{matrix} \right]=\boldsymbol{b}
Ax=⎣⎡1−1001−1001⎦⎤⎣⎡x1x2x3⎦⎤=⎣⎡x1x2−x1x3−x2⎦⎤=⎣⎡b1b2b3⎦⎤=b
从以上两式可以看出,矩阵A乘以向量
x
\boldsymbol{x}
x等同于矩阵
A
A
A的三个列向量的线性组合
x
1
u
+
x
2
υ
+
x
3
ω
x_1\boldsymbol{u}+x_2\boldsymbol{\upsilon}+x_3\boldsymbol{\omega}
x1u+x2υ+x3ω,即
A
x
A\boldsymbol{x}
Ax的结果就是矩阵A的各列的线性组合。
此外,我们也可以使用行的点乘来计算
A
x
A\boldsymbol{x}
Ax:
A
x
=
[
1
0
0
−
1
1
0
0
−
1
1
]
[
x
1
x
2
x
3
]
=
[
(
1
,
0
,
0
)
⋅
(
x
1
,
x
2
,
x
3
)
(
−
1
,
1
,
0
)
⋅
(
x
1
,
x
2
,
x
3
)
(
0
,
−
1
,
1
)
⋅
(
x
1
,
x
2
,
x
3
)
]
=
[
x
1
x
2
−
x
1
x
3
−
x
2
]
=
[
b
1
b
2
b
3
]
=
b
A\boldsymbol{x}=\left[\begin{matrix} 1 & 0 & 0\\ -1 & 1 & 0\\ 0 & -1 & 1\end{matrix} \right]\left[\begin{matrix} x_1 \\ x_2 \\ x_3\end{matrix} \right]=\left[\begin{matrix} (1,0,0) \cdot (x_1,x_2,x_3) \\ (-1,1,0) \cdot (x_1,x_2,x_3) \\ (0,-1,1) \cdot (x_1,x_2,x_3)\end{matrix} \right]=\left[\begin{matrix} x_1 \\ x_2-x_1 \\ x_3-x_2\end{matrix} \right]=\left[\begin{matrix} b_1 \\ b_2 \\ b_3\end{matrix} \right]=\boldsymbol{b}
Ax=⎣⎡1−1001−1001⎦⎤⎣⎡x1x2x3⎦⎤=⎣⎡(1,0,0)⋅(x1,x2,x3)(−1,1,0)⋅(x1,x2,x3)(0,−1,1)⋅(x1,x2,x3)⎦⎤=⎣⎡x1x2−x1x3−x2⎦⎤=⎣⎡b1b2b3⎦⎤=b
线性等式
前面我们是已知
x
1
,
x
2
,
x
3
x_1,x_2,x_3
x1,x2,x3,来计算等号右侧的
b
\boldsymbol{b}
b,那么,如果已知等号右侧的
b
\boldsymbol{b}
b,如何来求
x
\boldsymbol{x}
x呢?
旧问题: 计算线性组合
x
1
u
+
x
2
υ
+
x
3
ω
x_1\boldsymbol{u}+x_2\boldsymbol{\upsilon}+x_3\boldsymbol{\omega}
x1u+x2υ+x3ω为了得出
b
\boldsymbol{b}
b;
新问题:
u
,
υ
,
ω
\boldsymbol{u},\boldsymbol{\upsilon},\boldsymbol{\omega}
u,υ,ω的哪种组合可以生成指定的
b
\boldsymbol{b}
b。
很明显,这是一个互逆的问题。将等式
A
x
=
b
A\boldsymbol{x}=\boldsymbol{b}
Ax=b改写成我们熟悉的方程式组为:
{
x
1
=
b
1
−
x
1
+
x
2
=
b
2
−
x
2
+
x
3
=
b
3
\begin{cases} x_1&&&&&=&b_1&\\ -x_1&+&x_2&&&=&b_2& \\ &-&x_2&+&x_3&=&b_3 \end{cases}
⎩⎪⎨⎪⎧x1−x1+−x2x2+x3===b1b2b3
可轻易对该方程组求解:
{
x
1
=
b
1
x
2
=
b
1
+
b
2
x
3
=
b
1
+
b
2
+
b
3
\begin{cases} x_1=&b_1&\\ x_2=&b_1&+&b_2& \\ x_3=&b_1&+&b_2&+&b_3& \end{cases}
⎩⎪⎨⎪⎧x1=x2=x3=b1b1b1++b2b2+b3
写成矩阵形式为:
x
=
A
−
1
b
\boldsymbol{x}=A^{-1}\boldsymbol{b}
x=A−1b,我们将
A
−
1
A^{-1}
A−1称作
A
A
A的逆矩阵,此时的
A
A
A为可逆矩阵。
多个向量的独立和非独立性
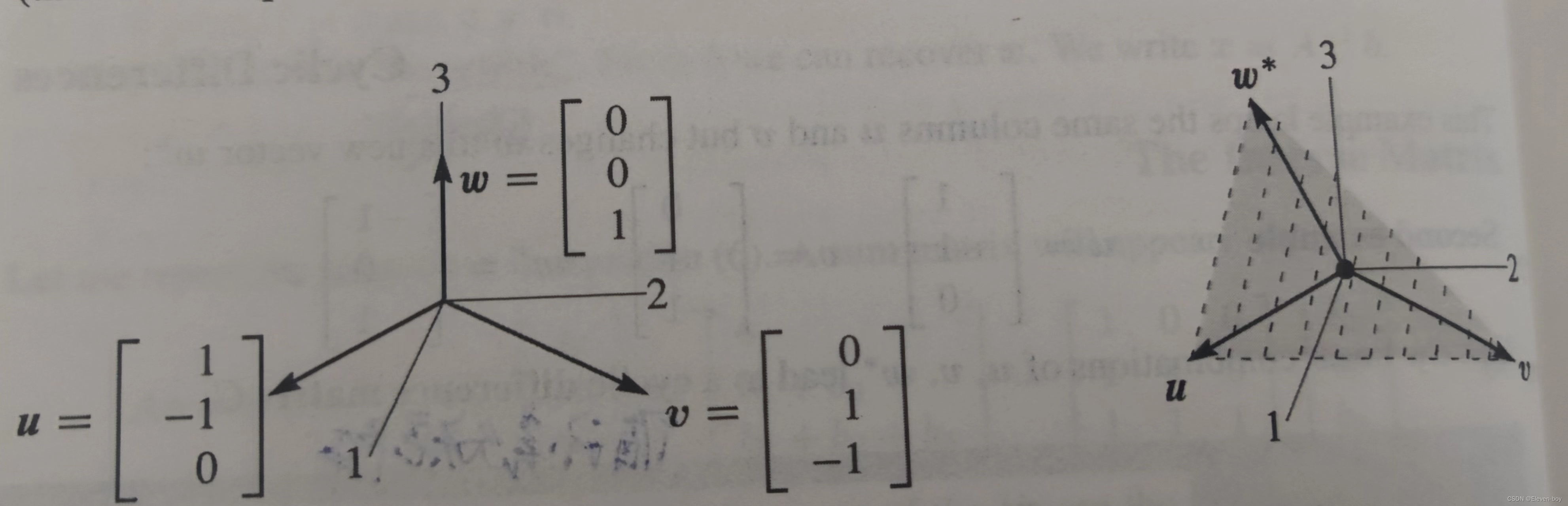
如上图所示,左右两个坐标系里向量
u
、
υ
\boldsymbol{u}、\boldsymbol{\upsilon}
u、υ是一样的,这两个向量的线性组合构成一个同样的二维平面,关键问题是第三个向量是否在这个平面里:
独立性:
ω
\boldsymbol{\omega}
ω不在
u
、
υ
\boldsymbol{u}、\boldsymbol{\upsilon}
u、υ构成的平面中,即:
只有当
x
1
=
0
,
x
2
=
0
、
x
3
=
0
x_1=0,x_2=0、x_3=0
x1=0,x2=0、x3=0时,才满足等式
x
1
u
+
x
2
υ
+
x
3
ω
=
0
x_1\boldsymbol{u}+x_2\boldsymbol{\upsilon}+x_3\boldsymbol{\omega}=\boldsymbol{0}
x1u+x2υ+x3ω=0
如果矩阵
A
A
A的列是独立的,则
A
x
=
0
A\boldsymbol{x}=\boldsymbol{0}
Ax=0只有一个解,
A
A
A被称作可逆矩阵(非奇异矩阵)。
非独立性:
ω
∗
\boldsymbol{\omega^*}
ω∗在
u
、
υ
\boldsymbol{u}、\boldsymbol{\upsilon}
u、υ构成的平面中,即:
存在多组
x
1
,
x
2
,
x
3
x_1,x_2,x_3
x1,x2,x3,满足
x
1
u
+
x
2
υ
+
x
3
ω
∗
=
0
x_1\boldsymbol{u}+x_2\boldsymbol{\upsilon}+x_3\boldsymbol{\omega^*}=\boldsymbol{0}
x1u+x2υ+x3ω∗=0
如果矩阵
C
C
C的列是非独立的,则
C
x
=
0
C\boldsymbol{x}=\boldsymbol{0}
Cx=0存在多个解,矩阵
C
C
C被称作奇异矩阵。
4、参考
[1] Introduction Linear Algebra,Fifth Edition,Giibert Strang.