1 摩擦力特性分析

摩擦力的大小是多种因素共同作用的结果，例如相接触物体的材质、相对速度、润滑情况以及接触面的几何形状、材料和布局等。由于物体的实际表面并非绝对平滑，表现为摩擦表面一些突出的微小的点相互接触，称为“突点”。Stribeck 等研究人员通过观察摩擦现象，发现从静止开始加速直至达到稳态速度时，如图 2-5 所示，摩擦力在特性曲线中主要包括静摩擦、边界润滑、部分流体润滑和完全流体润滑四个阶段[47]。

1. 第一阶段为静摩擦阶段，物体相互接触从而在接触面产生弹性变形—预滑动 位移，随即出现了一种约束力—静摩擦力，与速度无关。
2. 第二阶段为边界润滑阶段，因为接触面间相对运动速度极低，所以在接触面间无法建立液体薄膜。研究人员发现摩擦特性曲线的形状、系统低速爬行问题都和边界润滑密切相关。
3. 第三阶段为部分流体润滑阶段，物体发生相对运动其接触面间形成液体薄膜，由于法向压力的作用，使得部分润滑液被挤出接触面，所以仍存在固体接触区域，摩擦记忆现象在此阶段较为突出。
4. 第四阶段为完全流体润滑阶段，由于接触面间完全形成液体薄膜，不存在固体接触，所以此时摩擦力开始减小，但是粘滞摩擦特性随速度的提高愈发显著，摩擦力随相对运动速度的增大而增大。

1.1 预滑动特性及摩擦滞回

被施加切向力的物体会产生微小的位移，在数百纳米至数十毫米之间，其大小与正压力、摩擦材料、表面形貌等有关，而预滑动摩擦就发生在位移范围内。此时速度几乎为零，但接触面间的关联结由于相互牵扯产生弹性变形，所以存在相对运动的趋势。所以，摩擦力与相对运动速度关系不大，而是与预滑动位移有关。当撤去外力后，位移不能恢复到初始位置，从而形成滞回。

1.2 非局部记忆效应

实验发现，预滑动阶段的摩擦滞回不仅与当前位移有关，而且还取决于之前的位移信息。即系统当前时刻的输出，是当前系统输入和过去时刻系统输入或输出共同作用的结果。

1.3 临界摩擦力

随位移增大，摩擦力也持续增加。直到某一时刻，摩擦从预滑动转为开始宏观滑动，摩擦力在期间有所下降，其最大值为临界摩擦力，与外加作用力的增长速率相关。速度在±5mm/s 之间改变时，摩擦力的变化情况如下图 2-6 所示。

1.4 低速爬行现象

爬行现象分析简图如图 2-7 所示，以速度 v 开始驱动物体 m 时，静摩擦力导
致其仍静止不动，当驱动力超过最大静摩擦力时，物体开始运动，启动瞬间物体加速，弹簧开始减小压缩量。当驱动力降低到与滑动摩擦力相等时，由于物体惯性使得弹簧继续减小压缩量；当弹簧驱动力小于动摩擦力时，物体开始减速。若物体惯性太大则驱动力不能够使物体继续运动从而发生停顿，上述过程重复发生，就导致了系统的爬行现象。

1.5 Stribeck 效应

研究表明，在定常速润滑条件下，当摩擦进入宏观滑动阶段时，随速度的不断增大，摩擦力先下降到一个极小值，然后随速度增大而增大。摩擦力随运动物体速度变化呈现出来的变化规律，即为 Stribeck 效应。

1.6 摩擦滞后特性

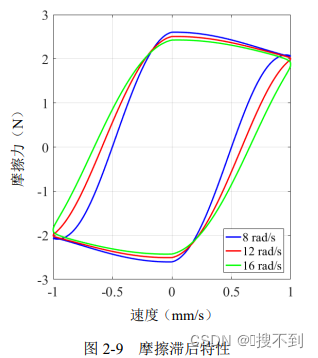
实验中发现，摩擦力在系统加速时要比减速时略大一些，其依赖于加速度的符号及其数值上的变化，说明摩擦力大小不仅与系统速度有关，还与加速度密切相关。不同速度和加速度下的摩擦力变化情况如图 2-9 所示，在系统加减速下摩擦力的不同表现，称为摩擦滞后特性。

1.7 法向与切向摩擦力的耦合

物体在摩擦过程中，接触界面的法向由于不光滑，也存在相对运动。系统变量和摩擦力在法向与切线方向间的耦合关系，是研究摩擦力的关键。

2 摩擦力数学模型

静态模型主要表明摩擦力只与速度有关，动态模型表明摩擦力不仅与速度有关，而且与位移有着密切的关系，可以相对真实且全面地反映摩擦现象，其实际应用价值更好。

2.1 静态摩擦模型

经典的库仑摩擦模型的数学形式。当外力小于静摩擦力时，速度为零，不会产生相对运动；当外力大于静摩擦力时，速度不为零，存在一恒定摩擦力阻碍运动的进行。可知，$F_f$与$v$方向相反，与$F_N$成正比，但该模型不能反映出静摩擦力的大小，如图 2-10 所示。
$\begin{array}{rl}{F}_f(\nu )& =F_c\mathrm{sgn}(\nu )\\ & \\ F_c& =\mu F_N\end{array}$
式中：
$\mu$表示摩擦系数；
$v$表示相对运动速度(m/s)；
$F$