目录
一、背景
二、代码
一、背景
数值方法被用于创建电影、游戏或其他媒体中的计算机图形。例如,生成“逼真”的烟雾、水或爆炸等动画。本文内容是对头发的模拟,要求考虑重力、风力的影响。
假设:
1、人的头部是一个半径为10厘米的球体。
2、每根头发都与球体的表面垂直相交。
3、作用在每根头发上的力包括重力(在-z方向上)和恒定的风力(在+x方向上)。
二、代码
#导入python包
import numpy as np
import matplotlib.pyplot as plt
import scipy.integrate
import scipy.optimize
def rhs_func_wrapper(f_x, f_g):
'''
输入:f_x风力、f_g重力
输出:函数rhs_func,用于包装常微分方程
'''
def rhs_func(s, y):
'''
输入:
s弧度(自变量)
y即[角度θ,梯度u](因变量)
'''
theta = y[0]
u = y[1]
dyds = np.zeros_like(y)
dyds[0] = u #一阶导
dyds[1] = s * f_g * np.cos(theta) + s * f_x * np.sin(theta) #二阶常微分方程,对应方程(3a)
return dyds
return rhs_func
def shot(u0, theta_0, L, rhs_func):
'''
解决边界值问题(BVP)
返回:s弧长、y包含角度和梯度的数组、sol是OdeSolution对象,表示常微分方程的解(描述弧长s和角度θ之间关系)
'''
y0 = np.array([theta_0, u0])
interval = [0, L]
solution = scipy.integrate.solve_ivp(rhs_func,
interval, #rhs_func中参数s的范围
y0, #初始条件
max_step=1e-2, #设置步长
dense_output=True) #用于生成sol,可以用于在任意点插值解
s, y, sol = solution.t, solution.y, solution.sol
return s, y, sol
def shot_error_wrapper(theta_0, L, rhs_func):
'''
计算误差
'''
def shot_error(u0):
s, y, sol = shot(u0, theta_0, L, rhs_func)
phi = y[1, -1] #提取二维数组y中的梯度的最后一个元素,作为误差
return phi
return shot_error
def coordinate_rhs_func_wrapper(theta_s):
'''
计算头发坐标的导数
输入:theta_s表示一个描述弧长s和角度θ之间关系的OdeSolution对象
'''
def coordinate_rhs_func(s, y):
'''
输入:弧长s、y表示坐标(x,z)
'''
dyds = np.zeros_like(y) #初始化一个与y相同大小的数组dyds,用于存储导数
theta = theta_s(s)[0] #计算弧长s对应的角度theta,通过调用theta_s(s)获取,并取得返回值的第一个元素
dyds[0] = np.cos(theta) #求导公式
dyds[1] = np.sin(theta) #求导公式
return dyds
return coordinate_rhs_func
def hair_bvp_2d(theta_0_list, L, R, f_x, f_g=0.1):
'''
输入:theta_0_list初始角度列表,L头发长度,R人头半径,f_x风力,f_g重力(默认为0.1)
'''
rhs_func = rhs_func_wrapper(f_x, f_g)
x_list = [] #初始化两个空列表用于存储解
z_list = []
for theta_0 in theta_0_list: #对于每根头发的初始角度theta_0进行以下步骤
shot_error = shot_error_wrapper(theta_0, L, rhs_func)
u0 = scipy.optimize.brentq(shot_error, -10, 10) #在-10~10区间内找到误差最小的初始梯度u0
s, y, sol = shot(u0, theta_0, L, rhs_func)
coordinate_rhs_func = coordinate_rhs_func_wrapper(sol)
y0 = np.array([R * np.cos(theta_0), R * np.sin(theta_0)]) #设置初始条件
interval = [0, L]
solution = scipy.integrate.solve_ivp(coordinate_rhs_func, interval, y0,
max_step=1e-2)
x_list.append(solution.y[0]) #402个横坐标
z_list.append(solution.y[1]) #402个纵坐标
x = np.array(x_list)
z = np.array(z_list)
return x, z
def plot_hairs(x, z, R, title):
#画人头:半径为10的圆,颜色为blue
theta_list = np.linspace(0, 2 * np.pi, 50)
x_head = R * np.cos(theta_list)
y_head = R * np.sin(theta_list)
plt.plot(x_head, y_head, c='blue')
#依次画每根头发,颜色为gray
for i in range(x.shape[0]):
x_coords = x[i, :]
z_coords = z[i, :]
plt.plot(x_coords, z_coords, c='gray')
ax = plt.gca() #获取坐标轴实例
ax.set_aspect(1) #纵横单位长度比例为1:1
plt.xlabel('x') #横坐标名称
plt.ylabel('z') #纵坐标名称
plt.title(title) #图的名称
plt.show() #打印出来
if __name__ == "__main__":
L = 4 #头发长度:4cm
R = 10 #人的头部,半径10cm
theta_0_list = np.linspace(0, np.pi, 20) #0-π按20等分切分
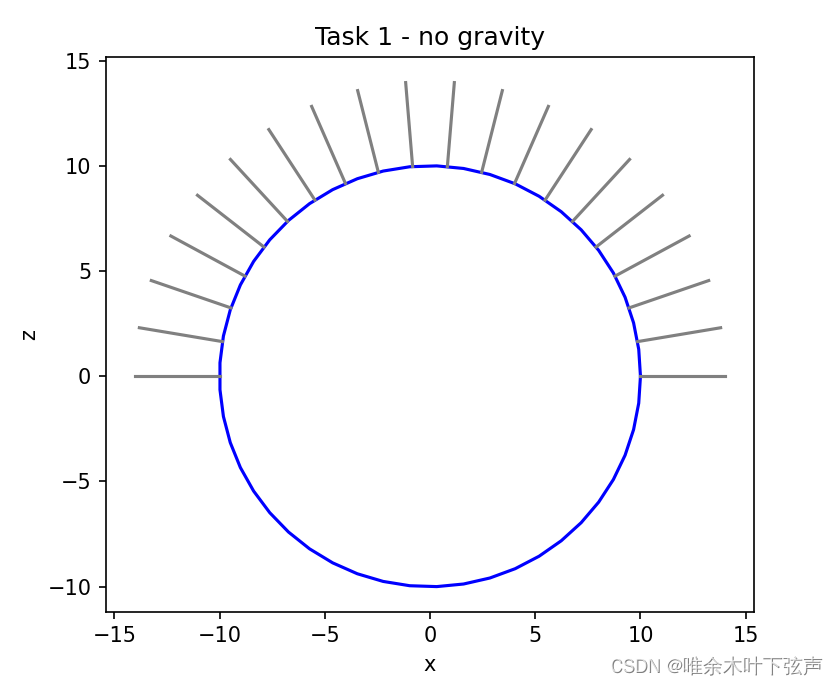
print('Task 1 - no gravity')
x, z = hair_bvp_2d(theta_0_list, L, R, 0, 0)
assert x.shape[0] == 20 and z.shape[0] == 20 and x.shape[1] == z.shape[1] #断言,如果不满足条件,则中断程序
plot_hairs(x, z, R, title='Task 1 - no gravity') #生成图像
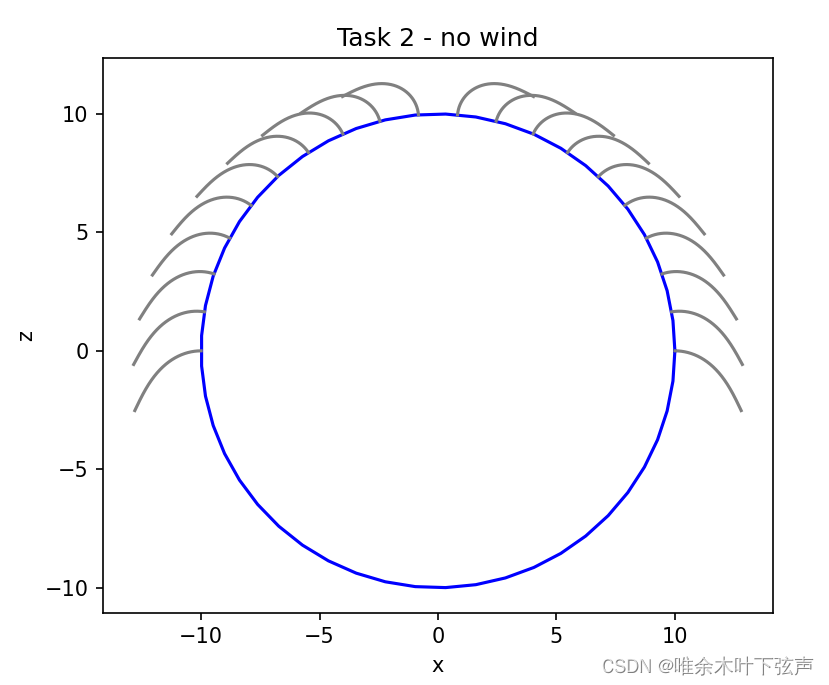
print('Task 2 - no wind')
x, z = hair_bvp_2d(theta_0_list, L, R, 0)
assert x.shape[0] == 20 and z.shape[0] == 20 and x.shape[1] == z.shape[1]
plot_hairs(x, z, R, title='Task 2 - no wind')
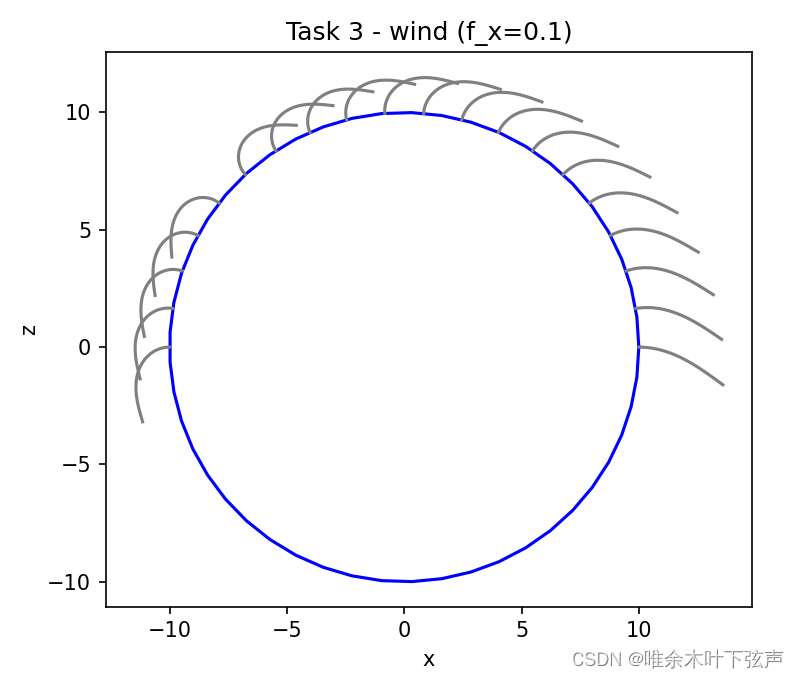
print('Task 3 - wind (f_x=0.1)')
x, z = hair_bvp_2d(theta_0_list, L, R, 0.1)
assert x.shape[0] == 20 and z.shape[0] == 20 and x.shape[1] == z.shape[1]
plot_hairs(x, z, R, title='Task 3 - wind (f_x=0.1)')
运行结果: