目录

快速排序

实现代码​​​​​​​

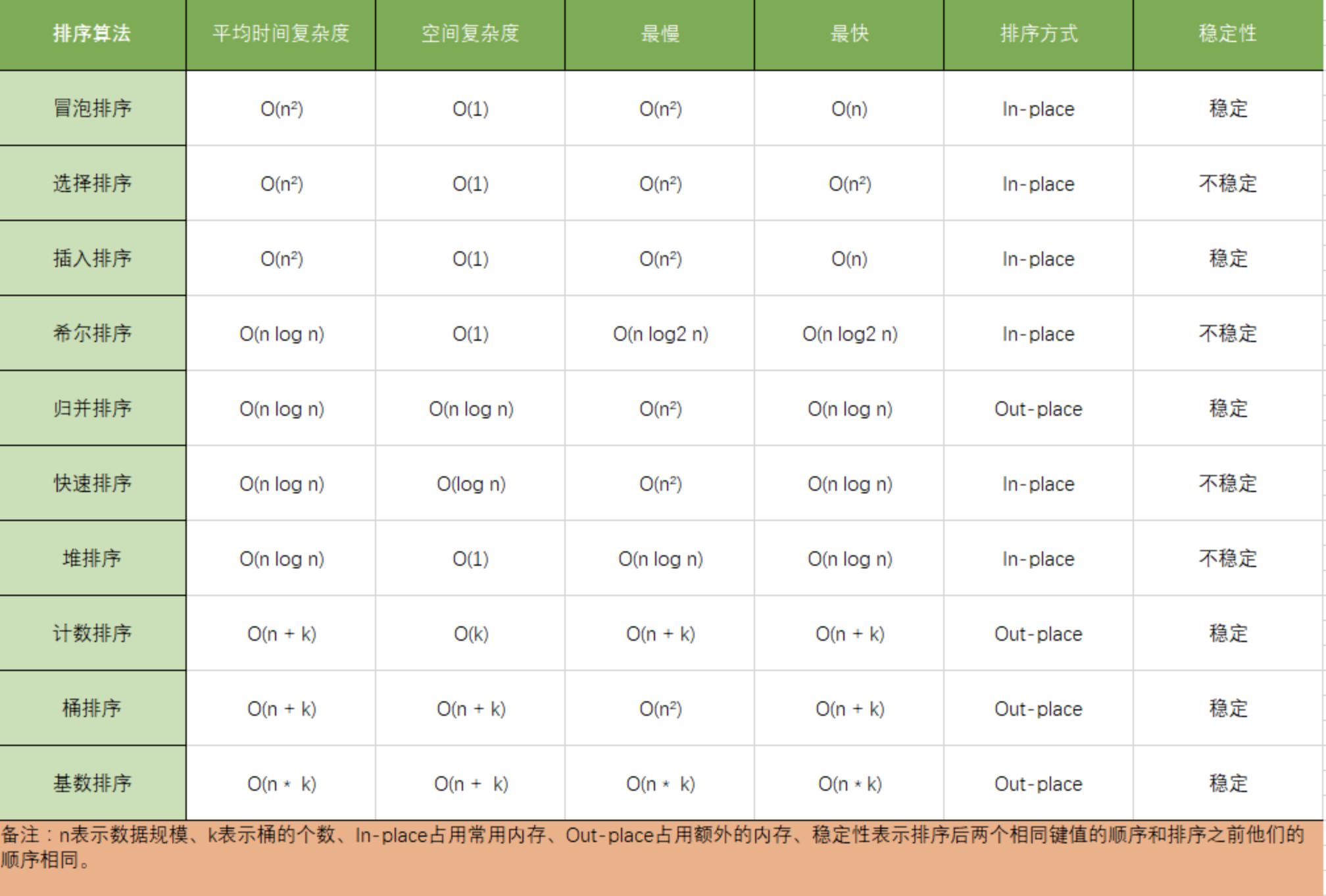
 时间复杂度

快排的优化

随机选择策略

三位取中法

非递归的快排

单向快排

---

快速排序

        快速排序算法是基于分治策略的一个排序算法，其基本思想是对于输入的子数组进行分解、递归求解，最后合并。

分解：以数组中左边第一个数作为基准元素，将数组划分为三段，nums[left,mid-1],nums[mid],nums[mid+1,right]，第一段中所有元素都比nums[mid]（这就是那个基准数）小，第三段中所有元素都大于等于基准数。

递归求解：递归调用快排分别对nums[mid]的左右两段分别排序

合并：当每一小段就地排序都排好序后，整个数组就已经排完了

实现代码

void Print(int* nums, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%-5d", nums[i]);
	}
	printf("\n");
}
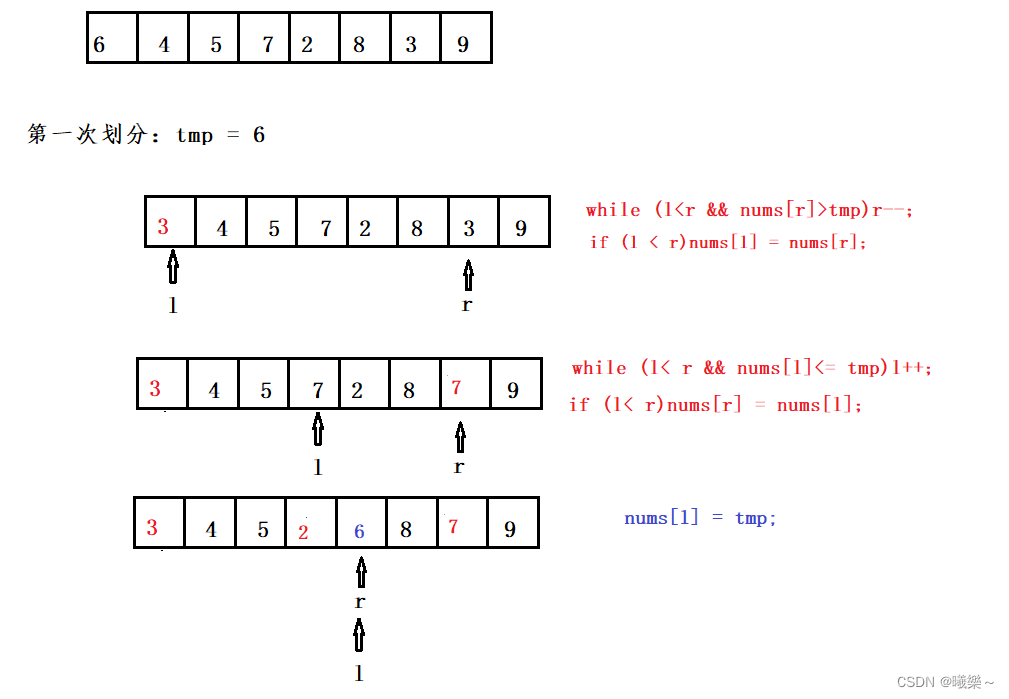
int Partition(int* nums,int left,int right)
{
	int l = left, r = right;
	int tmp = nums[l];
	while (l < r)
	{//确保l，r不错位每个都要判断l<r
		while (l<r && nums[r]>tmp)r--;//先找右边比tmp小的值
		if (l < r)nums[l] = nums[r];
		while (l< r && nums[l]<= tmp)l++;//在找左边比tmp大的值
		if (l< r)nums[r] = nums[l];
	}
	//l,r指针重合
	nums[l] = tmp;
	return l;
}
void QuickSort(int* nums, int left ,int right)
{
	if(left<right)
	{
		int mid = Partition(nums, left, right);//划分函数
		QuickSort(nums, left, mid - 1);
		QuickSort(nums, mid + 1, right);
	}
}

划分时一定要先从右边开始扫描 

 时间复杂度

         一般在问题规模为n时时间复杂度T(n)= Ο(nlogn)。最坏情况,数据从小到大或从大到小有序时T(n) =  Ο(n^2) 。

---

快排的优化

随机选择策略

      在快排的每一步当数组还没有被划分时，在数组中随机选出一个元素作为划分基准，划分基准随机则划分是比较对称的。用stand()指定一个随机起始点，然后将随机数模数组长度。因为这个right - left是相对位置的长度，但使用的下标rapos必须为绝对位置的下标，所以需要+left。

        将随机选择的基准值交换到第一个位置，然后再使用划分函数。

int RandomPartition(int* nums, int left, int right)
{
	srand(time(nullptr));//随机种子
	int rapos = rand() % (right - left + 1)+left;//取模
	std::swap(nums[left], nums[rapos]);//交换两个下标的值
	return Partition(nums, left, right);
}

---

三位取中法

        left ，right ，mid三个位置的元素取中间大小的元素作为基准值。如nums[left] = 12,nums[mid]=8,nums[right]=10;则取nums[right]作为基准。

struct Index
{
	int val;
	int index;
};
int MedionThree(int* nums, int left, int right)
{
	int mid = left + (right - left >> 1);
	struct Index idx[] = { {nums[left],left},{nums[mid],mid},{nums[right],right} };
	for (int i = 0; i < 3; i++)//找到中间大的数放到数组头做基准值
	{
		switch(i)
		{
		case 0:
			if ((idx[i].val - idx[1].val) * (idx[i].val - idx[2].val) < 0) 
			{ std::swap(nums[idx[i].index], nums[left]); }
			break;
		case 1:
			if ((idx[i].val - idx[0].val) * (idx[i].val - idx[2].val) < 0)
			{
				std::swap(nums[idx[i].index], nums[left]);
			}
			break;
		case 2:
			if ((idx[i].val - idx[0].val) * (idx[i].val - idx[1].val) < 0)
			{
				std::swap(nums[idx[i].index], nums[left]);
			}
			break;
		}
	}
	return Partition(nums, left, right);
}

---

非递归的快排

算法递归的部分在于划分后将不同子串输入进去继续划分。非递归时可以将子串的边界装在队列中，之后依次取出作为划分的左右边界。当队列为空，即划分完所有的以后结束。

void QuickSort(int* nums, int left, int right)
{
	queue<int> qu;//队列
	qu.push(left);
	qu.push(right);
	while(!qu.empty())
	{
		int sleft = qu.front(); qu.pop();//取队头，出left
		int sright = qu.front(); qu.pop();
		int mid = Partition(nums, sleft, sright);
		if (sleft < mid - 1)//左边有一个以上元素，仍需划分
		{
			qu.push(sleft);
			qu.push(mid - 1);
		}
		if (mid + 1 < right)
		{
			qu.push(mid + 1);
			qu.push(sright);
		}
	}
}

---

单向快排

 一般的快速排序都是左右两个指针向中间找基准值应放的位置划分的，而单向快速排序是从一边开始的，此方法可以用于单链表的快速排序。

取第一个值为基准值，如上为6，int tmp = 6；

slow为第一个元素的下标，fast为第二个元素的下标（单链表中这里为指针）

fast++，如果元素小于基准值tmp,则slow先++，然后nums[slow],nums[fast]再交换，这样可以保证slow下标左边元素的值都小于等于tmp；

当fast遍历完数组后，nums[left]与nums[slow]交换，此时slow即为mid（划分的中间段）。

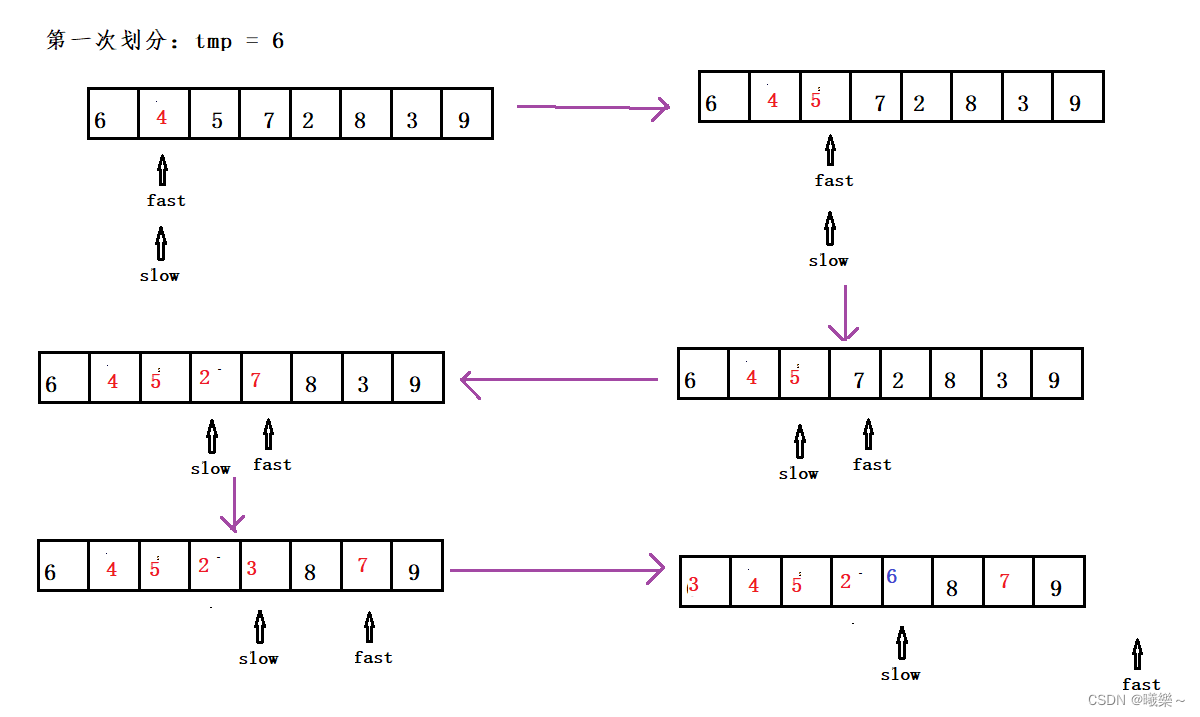
代码：

int Partition(int* nums, int left, int right)
{
	int fast, slow;
	slow = left;
	fast = slow;
	int tmp = nums[left];
	while(left < right)
	{
		fast++;
		if (fast > right)
		{
			std::swap(nums[left], nums[slow]);
			break;
		}
		if (nums[fast] < tmp)
		{
			slow++;
			std::swap(nums[slow], nums[fast]);
		}
	}
	return slow;
}
void QuickSort(int* nums, int left, int right)
{
	if (left < right)
	{
		int mid = Partition(nums, left, right);
		QuickSort(nums, left, mid - 1);
		QuickSort(nums, mid + 1, right);
	}
}