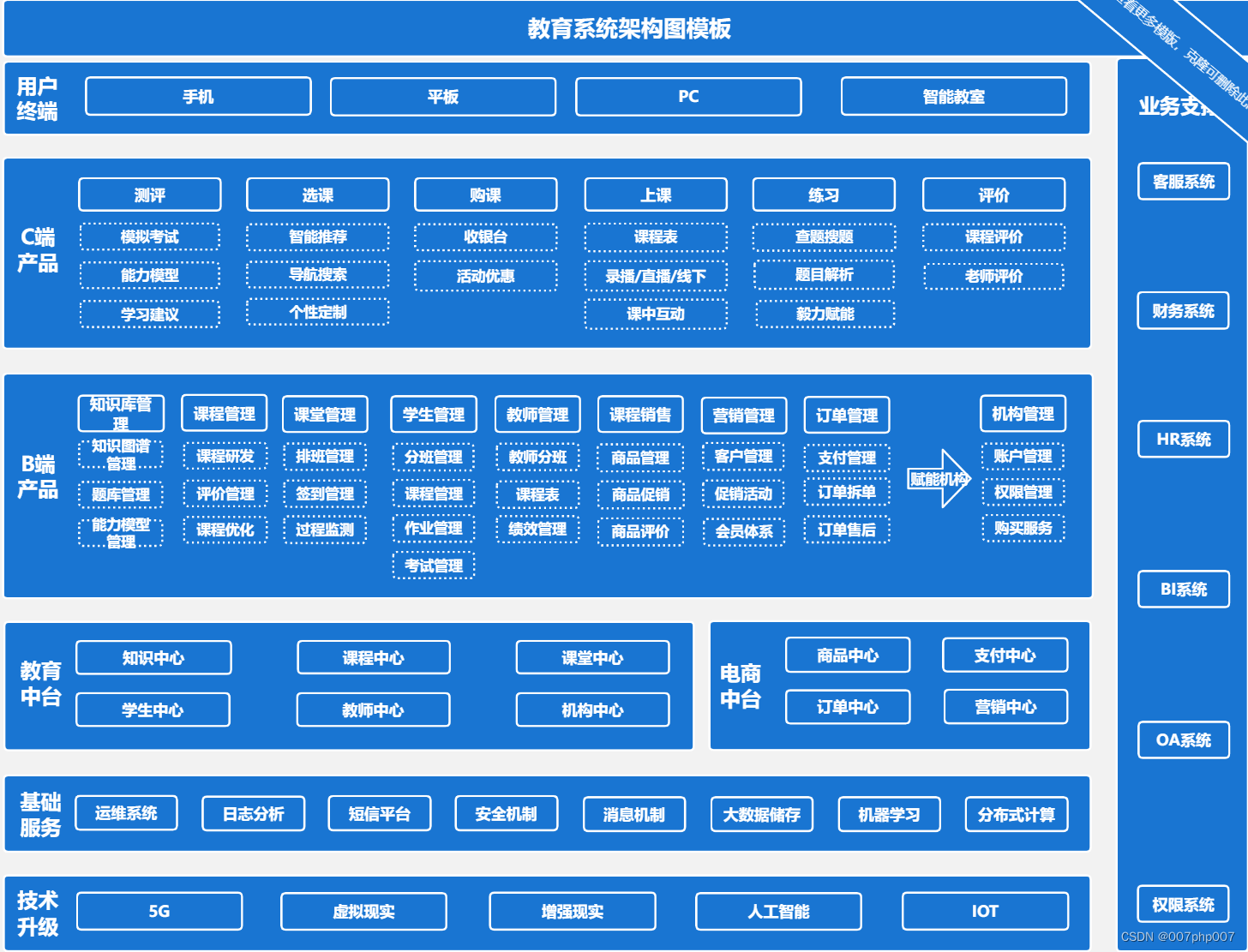
一、定义

1.栈的定义：

栈是只允许在一端进行插入或删除的线性表。首先栈是一种线性表，但限定这种线性表只能在某一端进行插入和删除操作。

• 栈顶（Top）:线性表允许进行插入删除的那一端；
• 栈底 (Bottom) ：固定的，不允许进行插入和删除的另一端；
• 空栈 ：不含任何元素；

栈又有两种书写形式：数组栈和链式栈，两种都可以，非要选一种，数组栈更好，虽然会造成一定的内存空间浪费，但是链式栈太麻烦。

链式栈栈顶的选择：

• 如果用尾做栈顶，尾插尾部删，要设计成双向链表，否则删除数据效率变低；
• 如果用头做栈顶，头插头删就可以设计成单链表。

自己理解了一下栈这个概念，就可以看做一个弹夹式手枪，先放进去的子弹要最后才能被打出来，最后放进去的子弹，是第一个被打出来。

栈的插入操作，叫做进栈，也称压栈、入栈。类似子弹入弹夹。

栈的删除操作，叫做出栈，有点也叫做弹栈。如同弹夹里的子弹出来。

2,进栈出栈的变化形式：

最先进栈的元素，是不是只能是最后出栈呢？我才开始认为这句话没问题，但是在看到书本解析时我才知道这句话是不对的。例如：若3、2、1进栈，那么出栈不止可以3、2、1，也可以是3进，3出，2进，2出，1进，1出，那么出栈就是1、2、3。这样不同的出栈次序约有5种。所以可以做出总结：最先进栈的元素不一定最后出栈。

二、栈的抽象数据类型：

对于栈来说，理论上线性表的操作特性它都具备，可是由于它的特殊性，所以针对它的操作上会有些许变化。特别是插入和删除操作，我们理解为弹和压，更容易理解。

InitStack(*S)//初始化操作，建立一个空栈
DestroyStack(*S)//若栈存在，就销毁它
ClearStack(*S)//将栈清空
StackEmpty(*S)//若栈为空，返回true,否则返回false
GetTop(S,*e)//若栈存在且非空，用e返回S的栈顶元素
Push(*S,*e)//若栈S存在，插入新元素e到栈S中，并成为栈顶元素
Pop(*S,*e)//删除栈S中栈顶元素，并用e返回其值
StackLength(S)//返回栈S的元素个数

/* 链栈结构 */
typedef struct StackNode
{
    SElemType data;
    struct StackNode* next;
}StackNode, * LinkStackPtr;


typedef struct
{
    LinkStackPtr top;
    int count;
}LinkStack;

Status visit(SElemType c)
{
    printf("%d ", c);
    return OK;
}

/*  构造一个空栈S */
Status InitStack(LinkStack* S)
{
    S->top = (LinkStackPtr)malloc(sizeof(StackNode));
    if (!S->top)
        return ERROR;
    S->top = NULL;
    S->count = 0;
    return OK;
}

/* 把S置为空栈 */
Status ClearStack(LinkStack* S)
{
    LinkStackPtr p, q;
    p = S->top;
    while (p)
    {
        q = p;
        p = p->next;
        free(q);
    }
    S->count = 0;
    return OK;
}

/* 若栈S为空栈，则返回TRUE，否则返回FALSE */
Status StackEmpty(LinkStack S)
{
    if (S.count == 0)
        return TRUE;
    else
        return FALSE;
}

/* 返回S的元素个数，即栈的长度 */
int StackLength(LinkStack S)
{
    return S.count;
}

/* 若栈不空，则用e返回S的栈顶元素，并返回OK；否则返回ERROR */
Status GetTop(LinkStack S, SElemType* e)
{
    if (S.top == NULL)
        return ERROR;
    else
        *e = S.top->data;
    return OK;
}

/* 插入元素e为新的栈顶元素 */
Status Push(LinkStack* S, SElemType e)
{
    LinkStackPtr s = (LinkStackPtr)malloc(sizeof(StackNode));
    s->data = e;
    s->next = S->top;	/* 把当前的栈顶元素赋值给新结点的直接后继，见图中① */
    S->top = s;         /* 将新的结点s赋值给栈顶指针，见图中② */
    S->count++;
    return OK;
}

/* 若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR */
Status Pop(LinkStack* S, SElemType* e)
{
    LinkStackPtr p;
    if (StackEmpty(*S))
        return ERROR;
    *e = S->top->data;
    p = S->top;					/* 将栈顶结点赋值给p，见图中③ */
    S->top = S->top->next;    /* 使得栈顶指针下移一位，指向后一结点，见图中④ */
    free(p);                    /* 释放结点p */
    S->count--;
    return OK;
}

Status StackTraverse(LinkStack S)
{
    LinkStackPtr p;
    p = S.top;
    while (p)
    {
        visit(p->data);
        p = p->next;
    }
    printf("\n");
    return OK;
}

三、栈的顺序储存结构及实现：

1.栈的顺序储存结构：

既然栈是线性表的特例，那么栈的顺序储存其实也是线性表顺序储存的简化，我们简称为顺序栈。

顺序表是用数组来实现的，对于栈这种只能一头插入删除的线性表来说，用数组下标为0的一端作为栈底比较好，应为首元素都存在栈底，变化最小，所以让它做栈底。

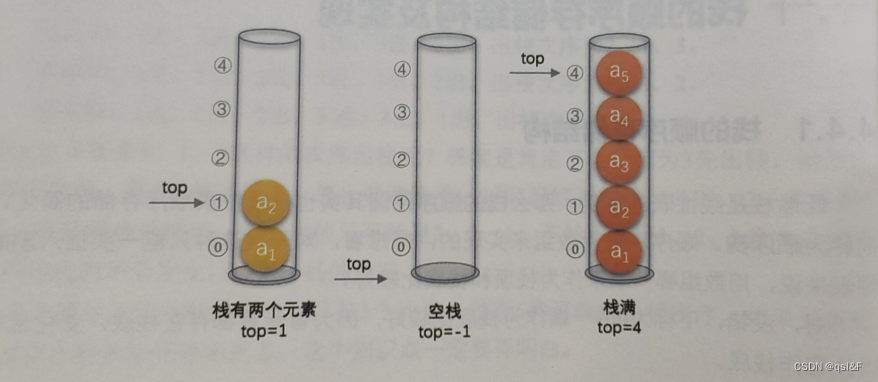
我们定义一个top变量来指示栈顶元素在数组中的位置，它可以变大变小。若储存栈的长度为StackSize，则栈顶位置top必须小于StackSize。当栈存在一个元素时，top等于0，因此通常把空栈的判定条件定为top等于-1。

栈的结构定义：

typedef int SElemType;
//顺序栈结构
typedef struct
{
	SElemType data[MAXSIZE];
	int top;//用于栈顶指针
}SqStack;

若有一个栈，StackSize是5，则栈普通情况、空栈和满栈的情况如下图：

2.栈的顺序储存结构——进栈操作

操作如图所示：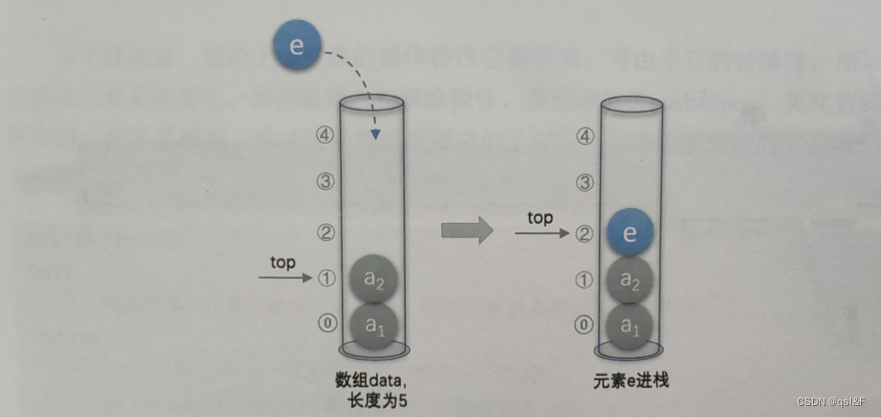

因此对于进栈操作push，其代码如下：

Status Push(SqStack* S, SElemType e)
//Status 是函数的类型，其值是函数结果状态代码，如OK等
{
	if (S->top == MAXSIZE - 1)
	{
		return ERROR;//这个说明栈满，无法再进栈
	}
	S->top++;//栈顶指针增加1
	S->data[S->top] = e; //赋值
	return OK;
}

Status 是函数的类型，其值是函数结果状态代码，如OK等。函数返回值只不过是时函数处理的状态，返回类型Status是一个整型，返回OK代表1，ERROR代表0。

typedef int Status;

3.栈的顺序储存结构——出栈操作

出栈操作pop，代码如下：

Status Pop(SqStack* S, SElemType* e)
{
	if (S->top == -1)
	{
		return ERROR;//空栈
	}
	*e = S->data[S->top];//将要删除的栈顶元素赋值给e
	S->top--;
	return OK;
}

四、两栈共享空间： 

栈的顺序储存还是很方便的，因为它只准栈顶进出元素，所以不存在线性表插入删除时需要移动元素的问题，不过它有一个很大的缺陷，就是必须事先确定数组存储空间大小，万一不够用了，就需要用编程手段来扩展数组的容量，非常麻烦。对于一个栈，我们也只能尽量考虑周全，设计出合适大小的数组来处理，但对于两个相同类型的栈，我们却可以做到最大限度地利用其事先开辟的储存空间来进行操作。

如果我们有两个类型相同的栈，我们为它们各自开辟了数组空间，极有可能是第一个已经满了，再进栈就溢出了，而另一个栈还有很多储存空间空闲，这又是何必呢？我们完全可以用一个数组来储存两个栈，充分利用这个数组占用的内存空间，只不过实现需要一些小技巧。

做法如下图：数组有两个端点，两个栈有两个栈底，让一个栈的栈底为数组的始端，即下标为零处，另一个栈为数组的末端，即下标为数组长度n-1处。这样，两个栈如果增加元素，就是两端点向中间延伸。

其实关键思路是：它们是在数组的两端，向中间靠拢。top1和top2是栈1和栈2的栈顶指针，可以想象，只要它们两不见面，两个栈就可以一直使用。

从这里分析出来，栈1为空时，就是top1等于-1时；而当top2等于n时，即是栈2为空时，那什么时候栈满呢？                              

咱们根据这个图，简单推理一下，就可以发现当栈2为空，也就是top1=n-1时也就是栈一满了；反之，当栈1为空栈时，top2等于0时，栈二满。但跟多情况，其实就是两栈见面之时，也就是两个指针之间相差1时，即top1+1==top2为栈满。（这个式子表达的是指针位置之间的关系）

两栈共享结构代码：

//两栈共享空间结构
typedef struct
{
	SElemType data[MAXSIZE];
	int top1;
	int top2;
}SqDoubleStack;

对于两栈共享push方法，我们除了要插入元素值参数外，还需要有一个判断是栈1还是栈2的栈号参数stackNumber。这个栈号参数我们可以理解为，准备向那个栈里加东西，方便后续操作。

//插入元素e为新的栈顶元素
Status Push(SqDoubleStack* S, SElemType e, int stackNumber)
{
	if (S->top1 + 1 == S->top2)//栈满
	{
		return ERROR;
	}
	else if (stackNumber == 1)//若栈1有元素进栈
	{
		S->data[++S->top1] = e;//先+1再赋值
		return OK;
	}
	else if (stackNumber == 2)//若栈2有元素进栈
	{
		S->data[--S->top2] = e;//先-1再赋值
		return OK;
	}
}

因为在代码开始时已经判断了是否有栈满的情况，所以后面的top1+1或top2-1是不用担心溢出的问题，

对于两栈共享空间pop方法，参数就只是判断栈1，栈2的参数stackNumber，代码如下：

//若栈不空，则删除栈顶元素，用e返回其值，并返回OK；否则返回ERROR
Status Pop(SqDoubleStack* S, SElemType* e, int stackNumber)
{
	if (stackNumber == 1)
	{
		if (S->top1 == -1)//栈1空栈，溢出
		{
			return ERROR;
		}
		*e = S->data[S->top1--];//先赋值，再--
	}
	else if (stackNumber == 2)
	{
		if (S->top2 == MAXSIZE)//说明栈2空栈，溢出
		{
			return ERROR;
		}
		*e = S->data[S->top2++];//先赋值，再++
	}
	return OK;
}

其实，我在学这个两栈共享空间这个概念的时候，我并不能理解它所存在的意义是什么？两个栈都在不停的增长很快就会因为栈满而溢出了。但是当我看过讲解之后，才知道，使用这样的数据结构，通常都是当两个栈的空间需求有相反关系时，也就是一个栈增长时另一个栈在缩短的情况。这样使用两栈共享空间储存方法才有较大意义。所以解决问题要选择适当的方法，不然会让问题复杂化。

五、栈的链式储存结构及实现

1.栈的链式储存结构：

栈的链式储存结构，简称为链栈。想想看栈只是栈顶来做插入和删除工作，那么栈顶放在链表的头部还是尾部呢？而单链表刚好具有头指针，而栈顶指针也是必须，我们可以将其和二为一，所以比较好的方法是把栈顶放在单链表的头部，另外已经有了栈顶在头部了，单链表常用的头结点也就失去了意义，通常对于链栈来说，是不需要头结点的。

对于链栈来说基本上不存在栈满的情况，除非内存已经没有可以使用的空间，如果真的发生，那么此时计算机操作系统已经面临死机崩溃的情况，而不是这个链栈是否溢出的问题。

对于空栈来说，链表原定义是头指针指向空，那么链栈的空其实就是top=NULL的时候。

链栈的结构代码如下：

/* 链栈结构 */
typedef struct StackNode
{
        SElemType data;
        struct StackNode *next;
}StackNode,*LinkStackPtr;


typedef struct
{
        LinkStackPtr top;
        int count;
}LinkStack;

 链栈的绝大部分操作都和单链表相似，只是在插入和删除上，特殊了一些。

2.栈的链式储存结构——进栈操作

对于链栈的进栈push操作，假设元素值为e的新节点是s，top为栈顶指针，代码如下，

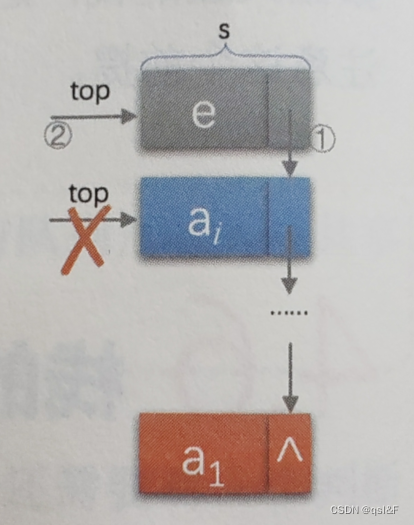
//插入元素e为新的栈顶元素
Status Push(LinkStack* S, SElemType e)
{
	LinkStackPtr s = (LinkStackPtr)malloc(sizeof(StackNode));
	s->data = e;
	s->next = S->top;
	S->top = s;
	S->count++;
	return OK;
}

这一串代码还是需要慢慢理解一下的，我才开始并不能够明白思路，我们先结合图来看一下，首先s是一个新的节点，我们需要给它适当的空间，类型就是LinkStackPtr，大小就是StackNode（一个节点）的大小，这个用法不熟悉的话，需要去了解一下malloc的用法，接着就是给新节点赋值为e，把当前的栈顶元素赋值给新节点的直接后继，再将新的节点s赋值给栈顶指针，这个单单的是看着，有点想不出来，看图！！！将栈顶元素赋值给新节点的直接后继是为了入栈操作，将它接上去，但是这样一操作栈顶处于第二个节点，所以我们需要将刚刚的新节点赋值给栈顶指针，让新节点成为新的栈顶，这样可以理解出，栈顶已经不再是之前的那个栈顶了，最后count++就不用说了，就这样入栈操作完成。

3.栈的链式储存结构——出栈操作

至于链栈的出栈pop操作，也是很简单的，看代码：

StackEmpty(*S)//若栈为空，返回true,否则返回false

//若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK，否则返回ERROK
Status Pop(LinkStack* S, SElemType* e)
{
	LinkStackPtr p;
	if (StackEmpty(*S))//判断是否为空
	{
		return ERROR;
	}
	*e = S->top->data;//用e储存将要删除的节点数据
	p = S->top;//将栈顶节点赋值给p
	S->top = S->top->next; //使得栈顶指针下移一位，指向后一节点
	free(p);//释放节点p
	S->count--;
	return OK;
}

这个操作还是很容易理解的，首先我们创建一个新节点p，这个p不需要提前给它空间，然后再判断链栈S是否为空，这之后我直接使用了之前写的函数，判断其是否为空，如果为空则不能继续进行删除操作，之后就是将要删除的数据储存在e中，要使用指针来进行赋值。接下来将栈顶节点赋值给p，然后将栈顶后移一位，指向后一节点，也就意味着原先的第二个节点变成了栈顶节点。最后释放p节点即可，count--就不用多说什么了。

六、栈的作用

我才学完栈这个概念的时候，感觉其实这些问题用链表和数组都能够轻易解决，那为什么要引入这样的数据结构呢？栈的引入简化了程序设计的问题，划分了不同关注层次，使得思考范围缩小，更加聚焦于我们所要解决的问题。

七、队列的定义

1. 队列是只允许在一段进行插入操作，而在另一端进行删除操作的线性表。
2. 队列是一种先进先出的线性表，简称FIFO。允许插入的一端称为队尾，允许删除的一段称为队头。假设队列是q=（a,b,c.....h,i,j,k），那么a就是队头元素，而k就是队尾元素，这样我们就可以删除时总是从a开始，而插入时，列在最后。这也比较符合我们通常的生活习惯，排在第一个的优先出列，最后来的当然排在队伍最后，如下图所示：

八、队列的抽象数据类型

同样是线性表，队列也有类似线性表的各种操作，不同的就是插入数据只能在队尾进行，删除数据只能在队头进行。

InitQueue(*Q);//初始化操作，建立一个空队列Q
DestoryQueue(*Q);//若队列Q存在，则销毁它
ClearQueue(*Q);//将Q队列清空
QueueEmpty(Q);//若队列Q为空，返回true，否则返回false
GetHead(Q, *e);//若队列Q存在且非空，用e返回队列Q的队头元素
EnQueue(*Q, e);//若队列Q存在，插入新元素e到队列Q中并成为队尾元素
DeQueue(*Q, *e);//删除队列Q中的队头元素，并用e返回其值
QueueLength(Q);//返回队列Q的元素个数

九、循环队列

1.队列顺序储存不足： 

我们假设一个队列有n个元素，则顺序储存的对垒需要建立一个大于n的数组，并把队列的所有元素储存在数组的前n个单元，数组下标为0的一端即是队头。所谓的入队操作，其实就是在队尾追加一个元素。如下图所示：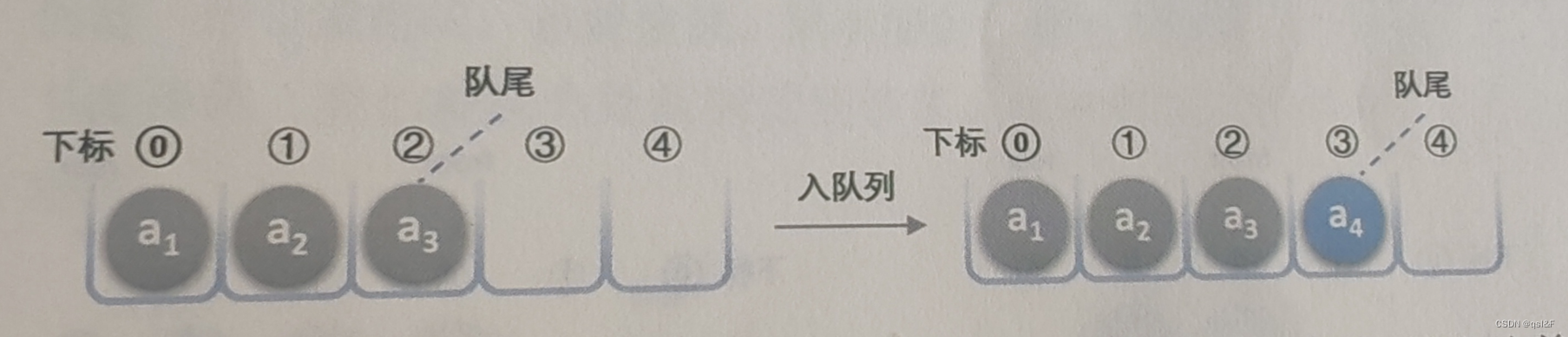

与栈不同的是，队列元素的出列是在队头，即下标为0的位置，那也就意味着，队列中的元素都得向前移动，以保证队列的队头，也就是下表为0的位置不为空。如下图所示：

可是想想，为什么出队列时一定要全部移动呢？如果不去限制队列的元素必须存储在数组的前n个单元这一条件，出队的可能性就会大大增加。也就是说，队头不需要一定在下标为0的位置如下图所示：

为了避免当只有一个元素时，队头和队尾重合使处理变得麻烦，所以引入两个指针，front指针指向队头元素，rear指针指向队尾元素的下一个位置，这样当front等于rear时，此队列不是还剩一个元素，而是空队列。

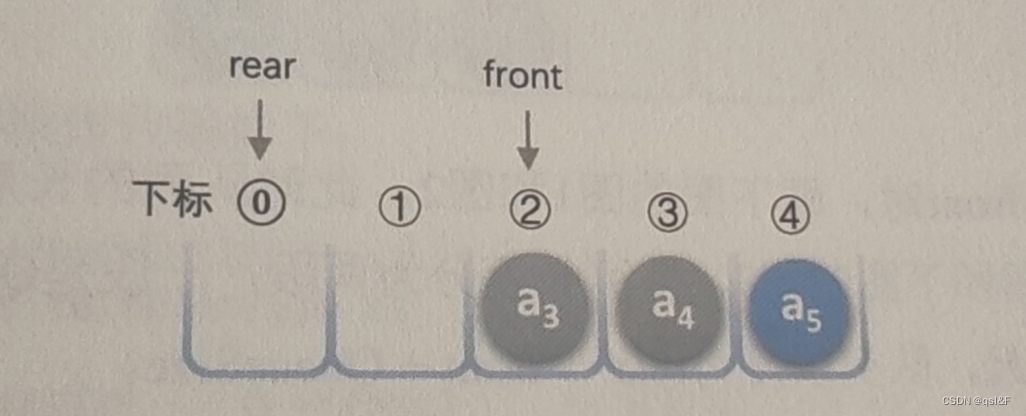
假设长度为5的数组，初始状态，如下图，front和rear指针均指向下标为0位置，而rear指针指向下标为4的位置，如下图所示：

出队a1、a2，则front指针指向下标为2的位置，rear不变，如下图所示，再入队a5，此时front不变，rear指针移动到数组之外，如下图所示：

数组之外又是哪里？问题不止于此，假设这个队列的总个数不超过5个，但目前如果接着入队的话，因数组，，末尾元素已经被占用，再向后加，就会产生数组越界的错误，可实际上，我们的队列在下标为0和1的地方还是空闲的。我们把这种现象叫做“假溢出”。

2.循环队列的定义：

所以解决假溢出的办法就是后面满了，就再从头开始，也就是头尾相接的循环。我们把这队列的这种头尾相接的顺序储存结构称为循环队列。

刚才的例子继续，上图的rear可以改为指向下标为零的位置，这样就不会造成指针指向不明的问题了，如下图所示：

接着入队a6，将它放置于下标为0处，rear指针指向下标为1处，如下图所示，若再有入队a7，则rear指针就与front指针重合，同时指向下标为2的位置，如下图所示：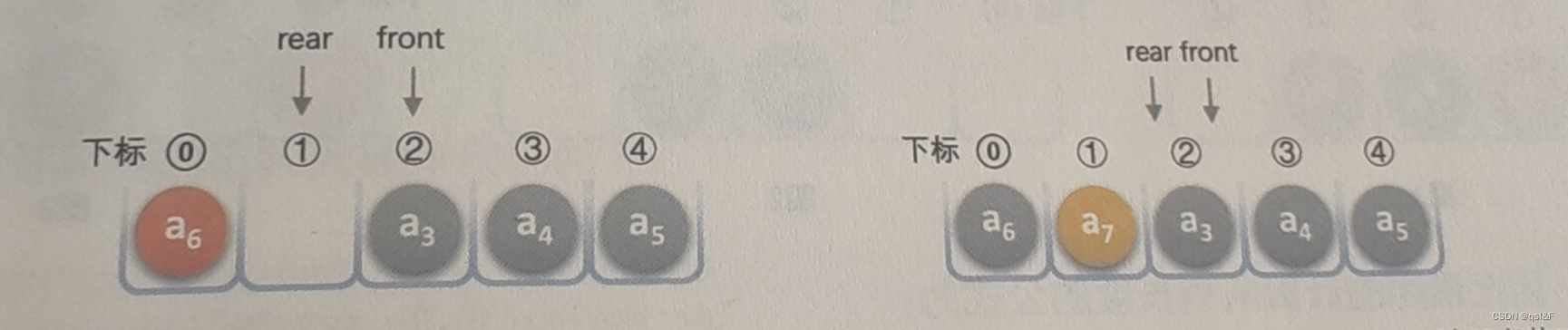

• 此时问题又出来了，我们刚才说，空队列时front等于rear，现在当队列满时，也是front等于rear，那么如何判断此时的队列是空还是满呢？
• 方法一：设置一个标志变量flag，当front=rear，且flag=0时为队列空；当ront=rear且flag=0时为队列满。
• 方法二：当队列空时条件为front=rear，当队列满时，我们修改其中的条件，保留一个元素空间。也就是说队列，满时，数组中还有一个空闲单元。例如下图所示，我们就认为此队列已经满了，也就是说，我们不允许上图的情况出现。

我们重点来讨论第二种方法，由于rear可能比front大，也可能比它小，所以尽管它们只相差一个位置就是满的情况，但也可能是相差整整一圈。所以若队列的最大尺寸为QueueSize，那么队列满的条件是（rear+1）%QueueSize==front（取模“%”的目的就是为了整合rear与front大小为一个问题）。自己尝试着算算就行了，可以理解的。

另外当rear>front时，此时队列的长度为rear-front，如下图所示。所以直接给一个总结性的公式：

（rear-front+QueueSize）%QueueSize，有了这些知识，实现循环队列代码就不难了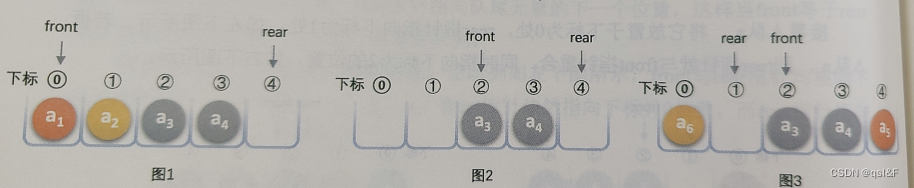

直接写代码：

typedef int Status;
typedef int QElemType;

//循环队列的顺序储存结构
typedef struct
{
	QElemType data[MAXSIZE];
	int front;//头指针
	int rear;//尾指针，若列队不空，指向列队尾元素的下一个
}SqQueue;

Status visit(QElemType e)
{
	printf("%d", e);
	return OK;
}


//初始化一个空队列
Status InitQueue(SqQueue* Q)
{
	Q->front = 0;
	Q->rear = 0;
	return OK;
}

//将Q清为空队列
Status ClearQueue(SqQueue* Q)
{
	Q->front = Q->rear = 0;
	return OK;
}

//若队列Q为空队列，则返回TRUE，否则返回FALSE
Status QueueEmpty(SqQueue Q)
{
	if (Q.front == Q.rear)//空队列的标志
	{
		return ERROR;
	}
	else
	{
		return OK;
	}
}

//返回Q的元素个数，也就是队列当前长度
int QueueLength(SqQueue Q)
{
	return (Q.rear - Q. front + MAXSIZE) % MAXSIZE;
}

//若队列不空，则用e返回Q的队头元素，并返回OK，否则返回ERROR
Status GetHead(SqQueue Q, QElemType* e)
{
	if (Q.front == Q.rear) /* 队列空 */
	{
		return ERROR;
	}
	*e = Q.data[Q.front];
	return OK;
}

//若队列不空，则删除Q中队头元素，用e返回其值
Status DeQueue(SqQueue* Q, QElemType* e)
{
	if (Q->front == Q->rear)			/* 队列空的判断 */
	{
		return ERROR;
	}
	*e = Q->data[Q->front];				/* 将队头元素赋值给e */
	Q->front = (Q->front + 1) % MAXSIZE;	/* front指针向后移一位置， */
	/* 若到最后则转到数组头部 */
	return  OK;
}

//从队头到队尾依次对队列Q中每个元素输出
Status QueueTraverse(SqQueue Q)
{
	int i;
	i = Q.front;
	while ((i + Q.front) != Q.rear)
	{
		visit(Q.data[i]);
		i = (i + 1) % MAXSIZE;//后移一位
	}
	printf("\n");
	return OK;
}

十、队列的链式储存结构及实现：

队列的链式储存结构，其实就是线性表单链表，只不过它只能尾进头出而已，我们把它简称为链队列，为了操作上的方便，我们将队头指针指向链队列的头结点，而队尾指针指向终端节点，如下图所示：

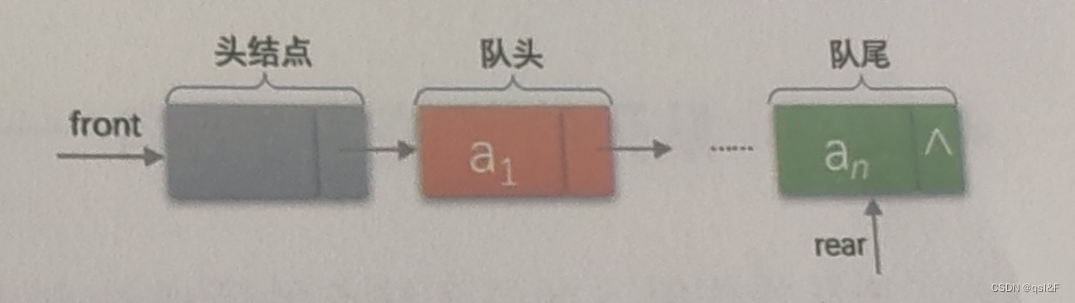
链队列的结构为：

typedef int Status; 

typedef int QElemType; /* QElemType类型根据实际情况而定，这里假设为int */

typedef struct QNode	/* 结点结构 */
{
   QElemType data;
   struct QNode *next;
}QNode,*QueuePtr;

typedef struct			/* 队列的链表结构 */
{
   QueuePtr front,rear; /* 队头、队尾指针 */
}LinkQueue;

1.队列的链式储存结构——入队操作

入队操作，其实就是在链表尾部插入节点，如下图所示：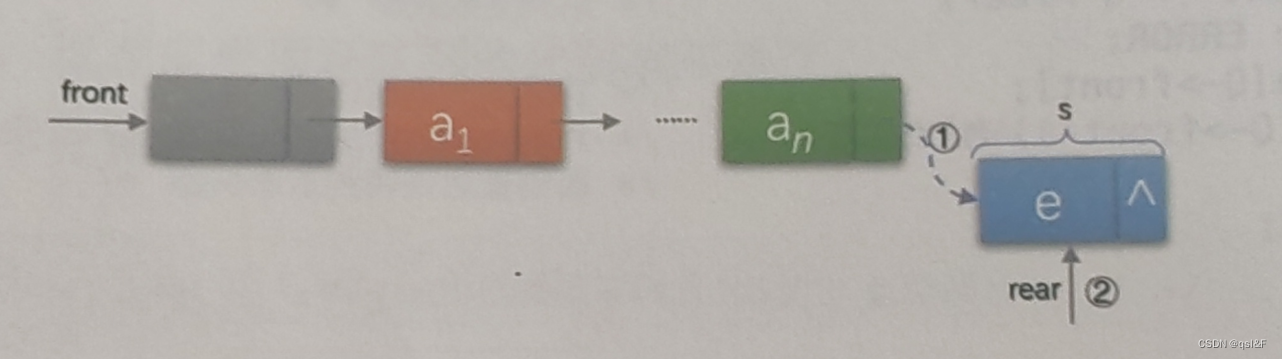

其代码如下：

/* 插入元素e为Q的新的队尾元素 */
Status EnQueue(LinkQueue *Q,QElemType e)
{ 
	QueuePtr s=(QueuePtr)malloc(sizeof(QNode));
	if(!s) /* 存储分配失败 */
		exit(OVERFLOW);
	s->data=e;
	s->next=NULL;
	Q->rear->next=s;	/* 把拥有元素e的新结点s赋值给原队尾结点的后继，见图中① */
	Q->rear=s;		/* 把当前的s设置为队尾结点，rear指向s，见图中② */
	return OK;
}

2.队列链式储存结构——出队操作

出队操作时，就是头结点的后继节点出队，将头结点的后继改为它后面的节点，若链表除头节点外只剩一个元素，则需要将rear指向头结点，如下图所示：

代码如下：

/* 若队列不空,删除Q的队头元素,用e返回其值,并返回OK,否则返回ERROR */
Status DeQueue(LinkQueue *Q,QElemType *e)
{
	QueuePtr p;
	if(Q->front==Q->rear)
		return ERROR;
	p=Q->front->next;		/* 将欲删除的队头结点暂存给p，见图中① */
	*e=p->data;				/* 将欲删除的队头结点的值赋值给e */
	Q->front->next=p->next;/* 将原队头结点的后继p->next赋值给头结点后继，见图中② */
	if(Q->rear==p)		/* 若队头就是队尾，则删除后将rear指向头结点，见图中③ */
		Q->rear=Q->front;
	free(p);
	return OK;
}

3.链队列的操作代码：

typedef int Status; 

typedef int QElemType; /* QElemType类型根据实际情况而定，这里假设为int */

typedef struct QNode	/* 结点结构 */
{
   QElemType data;
   struct QNode *next;
}QNode,*QueuePtr;

typedef struct			/* 队列的链表结构 */
{
   QueuePtr front,rear; /* 队头、队尾指针 */
}LinkQueue;

Status visit(QElemType c)
{
	printf("%d ",c);
	return OK;
}

/* 构造一个空队列Q */
Status InitQueue(LinkQueue *Q)
{ 
	Q->front=Q->rear=(QueuePtr)malloc(sizeof(QNode));
	if(!Q->front)
		exit(OVERFLOW);
	Q->front->next=NULL;
	return OK;
}

/* 销毁队列Q */
Status DestroyQueue(LinkQueue *Q)
{
	while(Q->front)
	{
		 Q->rear=Q->front->next;
		 free(Q->front);
		 Q->front=Q->rear;
	}
	return OK;
}

/* 将Q清为空队列 */
Status ClearQueue(LinkQueue *Q)
{
	QueuePtr p,q;
	Q->rear=Q->front;
	p=Q->front->next;
	Q->front->next=NULL;
	while(p)
	{
		 q=p;
		 p=p->next;
		 free(q);
	}
	return OK;
}

/* 若Q为空队列,则返回TRUE,否则返回FALSE */
Status QueueEmpty(LinkQueue Q)
{ 
	if(Q.front==Q.rear)
		return TRUE;
	else
		return FALSE;
}

/* 求队列的长度 */
int QueueLength(LinkQueue Q)
{ 
	int i=0;
	QueuePtr p;
	p=Q.front;
	while(Q.rear!=p)
	{
		 i++;
		 p=p->next;
	}
	return i;
}

/* 若队列不空,则用e返回Q的队头元素,并返回OK,否则返回ERROR */
Status GetHead(LinkQueue Q,QElemType *e)
{ 
	QueuePtr p;
	if(Q.front==Q.rear)
		return ERROR;
	p=Q.front->next;
	*e=p->data;
	return OK;
}


/* 插入元素e为Q的新的队尾元素 */
Status EnQueue(LinkQueue *Q,QElemType e)
{ 
	QueuePtr s=(QueuePtr)malloc(sizeof(QNode));
	if(!s) /* 存储分配失败 */
		exit(OVERFLOW);
	s->data=e;
	s->next=NULL;
	Q->rear->next=s;	/* 把拥有元素e的新结点s赋值给原队尾结点的后继，见图中① */
	Q->rear=s;		/* 把当前的s设置为队尾结点，rear指向s，见图中② */
	return OK;
}

/* 若队列不空,删除Q的队头元素,用e返回其值,并返回OK,否则返回ERROR */
Status DeQueue(LinkQueue *Q,QElemType *e)
{
	QueuePtr p;
	if(Q->front==Q->rear)
		return ERROR;
	p=Q->front->next;		/* 将欲删除的队头结点暂存给p，见图中① */
	*e=p->data;				/* 将欲删除的队头结点的值赋值给e */
	Q->front->next=p->next;/* 将原队头结点的后继p->next赋值给头结点后继，见图中② */
	if(Q->rear==p)		/* 若队头就是队尾，则删除后将rear指向头结点，见图中③ */
		Q->rear=Q->front;
	free(p);
	return OK;
}

/* 从队头到队尾依次对队列Q中每个元素输出 */
Status QueueTraverse(LinkQueue Q)
{
	QueuePtr p;
	p=Q.front->next;
	while(p)
	{
		 visit(p->data);
		 p=p->next;
	}
	printf("\n");
	return OK;
}