目录
一、引言
二、B树的基本定义
三、B树的性质与操作
1 查找操作
2 插入操作
3 删除操作
四、B树的应用场景
1 数据库索引
2 文件系统
3 网络路由表
五、哪些数据库系统不使用B树进行索引
1 列式数据库
2 图形数据库
3 内存数据库
4 NoSQL数据库
5 分布式数据库
六、总结
一、引言
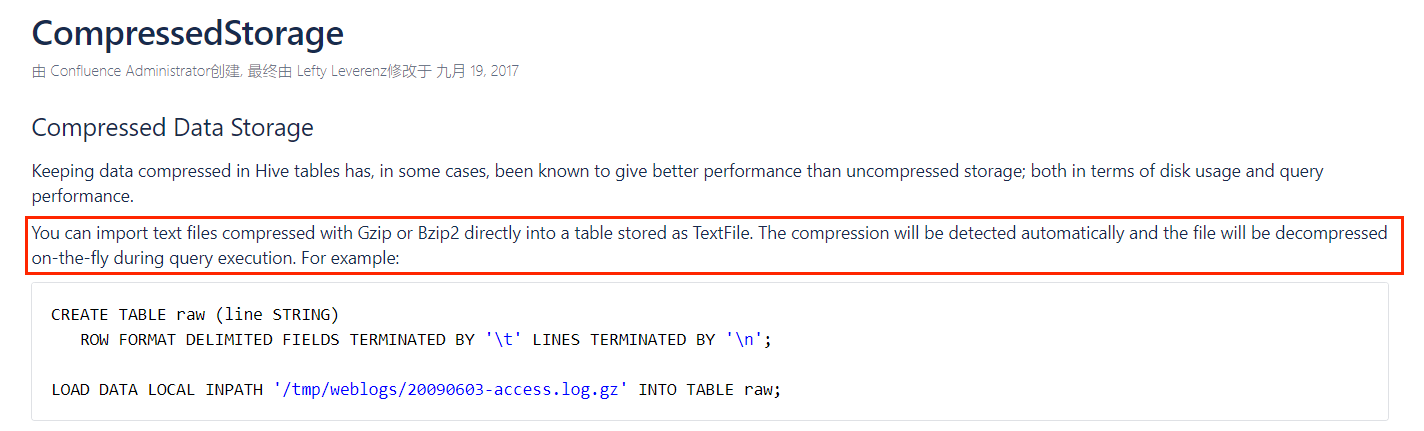
在计算机科学中,B树是一种自平衡的树,它能够保持数据有序,其插入与删除操作都能在对数时间内完成。
B树在数据库和文件系统的实现中尤为关键,因为它们能高效地保持数据有序,同时允许对数级别的插入、删除和查找操作。
B树相对于二叉搜索树的优势在于,它可以有效地利用存储空间,特别是在磁盘或类似的直接存取辅助设备中。
二、B树的基本定义
B树是一种平衡的多路搜索树,它满足以下条件:
- 所有叶子节点位于同一层。
- 每个非叶子节点包含n个关键字(k1, k2, ..., kn),其中n满足ceil(m/2) <= n <= m-1。对于每个关键字ki,ki < ki+1。
- 非叶子节点的子树指针p1, p2, ..., pn。其中所有关键字ki,i的子树指针pi指向的子树中所有关键字的值均大于ki且小于ki+1。
- 非叶子节点的子树个数=关键字个数+1。
- 所有关键字都出现在叶子节点的链表中(稠密索引),且链表中的节点是依次有序的。
其中,m是B树的阶数,它决定了树的最大和最小度数。一个m阶的B树,一个节点最多有m个子节点。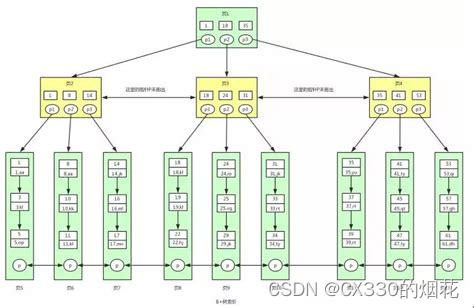
三、B树的性质与操作
B树作为一种自平衡树,其关键性质在于保持树的平衡,以保证查找、插入和删除操作的高效性。
1 查找操作
从根节点开始,根据键值比较进行路径选择,直到找到目标节点或到达叶子节点。B树的查找效率与树的高度相关,由于B树能够降低树的高度,因此查找效率较高。
- 从根节点开始搜索,找到合适的叶子节点进行插入。
- 如果插入后叶子节点关键字数不超过最大度数,则插入完成。
- 否则,需要分裂该叶子节点,并将中间关键字提升到父节点。
- 如果父节点也满了,则需要继续分裂并向上提升关键字,直到根节点或某个非满节点为止。
- 如果根节点也分裂了,则需要创建一个新的根节点,并将两个子树的根节点作为新根节点的子节点。
2 插入操作
当插入一个新元素时,首先找到合适的位置,如果节点未满,则直接插入;如果节点已满,则需要进行分裂操作,将节点中的部分元素移动到新的节点中,并更新父节点。
分裂操作可能导致父节点也满,此时需要递归地进行分裂和更新操作,直到根节点或某个非满节点为止。
- 从根节点开始搜索,找到包含要删除关键字的叶子节点。
- 如果该叶子节点的关键字数大于最小度数,则直接删除该关键字。
- 否则,需要从兄弟节点“借”一个关键字过来,或者与兄弟节点及父节点合并。
- 删除操作可能触发一系列的合并和调整操作,直到满足B树的性质为止
以下是B树插入操作的Python伪代码:
def insert(node, key):
if node is None:
return create_new_node(key)
i = node.find_position(key)
if key == node.keys[i]:
return node # Key already exists, no insertion
if node.is_leaf():
node.insert_non_full(i, key)
if node.is_full():
return split_node(node)
else:
return node
else:
child = node.children[i]
child = insert(child, key)
node.update_keys(i, child)
if child is not None:
return split_node(node) if node.is_full() else node
def split_node(node):
t = node.degree # Assume degree is set for the tree
mid = t - 1
new_node = create_new_node()
new_node.keys = node.keys[mid:]
new_node.children = node.children[mid+1:]
node.keys = node.keys[:mid]
node.children = node.children[:mid+1]
new_node.children[-1] = None if node.is_leaf() else split_node(node.children[mid+1])
node.parent = create_new_node() if node.parent is None else node.parent
node.parent.keys.append(node.keys[mid])
node.parent.children.append(new_node)
return node.parent
3 删除操作
删除操作相对复杂,因为需要保持B树的平衡性。当删除一个元素时,首先需要找到该元素所在的节点。
如果删除后节点不满,且兄弟节点有富余元素,则可以从兄弟节点借元素;如果兄弟节点也无富余元素,则需要进行合并操作,将当前节点与兄弟节点合并为一个新的节点,并更新父节点。合并操作可能导致父节点也不满,此时需要递归地进行合并和更新操作。
- 从根节点开始,根据关键字比较结果选择子节点进行搜索。
- 一直搜索到叶子节点,如果叶子节点包含要搜索的关键字,则搜索成功;否则搜索失败。
四、B树的应用场景
B树在计算机科学中有广泛的应用,特别是在处理大量数据时需要高效查找的场景中。以下是一些典型的应用场景:
1 数据库索引
在关系型数据库中,B树常被用作索引结构,以加快数据的查找速度。通过将数据按照键值排序并存储在B树中,数据库系统可以快速地定位到目标数据的位置。
2 文件系统
在文件系统中,B树也被用于目录结构的组织和查找。通过将目录项按照名称排序并存储在B树中,文件系统可以高效地定位到目标文件或目录。
3 网络路由表
在网络路由中,B树可以用于存储和查找路由信息。通过将IP地址或域名作为键值存储在B树中,路由器可以快速地找到目标地址的下一跳信息。
五、哪些数据库系统不使用B树进行索引
虽然B树及其变种(如B+树、B*树)是许多数据库系统实现索引的首选数据结构,但并非所有数据库系统都使用B树进行索引。以下是一些不使用B树进行索引的数据库系统的例子:
1 列式数据库
列式数据库,如Google的BigTable或Apache的Cassandra,它们的数据存储和索引方式与传统的行式数据库有所不同。这些系统通常基于键值对或列族进行数据存储和检索,因此可能不会使用传统的B树索引。
2 图形数据库
图形数据库,如Neo4j,专注于表示和查询图形结构的数据。它们通常使用专门的图算法和索引结构来加速查询,而不是传统的B树索引。
3 内存数据库
一些内存数据库,如Redis或Memcached,它们的数据主要存储在RAM中,以提供极快的读写速度。这些系统通常使用哈希表或其他内存友好的数据结构来支持快速查找,而不是B树。
4 NoSQL数据库
许多NoSQL数据库,如MongoDB(在某些情况下)和Cassandra,不依赖于传统的B树索引。MongoDB支持多种索引类型,包括哈希索引和地理空间索引,这些索引类型可能不使用B树结构。
5 分布式数据库
分布式数据库系统,如Spanner或CockroachDB,需要处理跨多个物理节点的数据。这些系统通常使用更复杂的索引和分区策略,可能不完全依赖于B树。
需要注意的是,即使某些数据库系统不使用B树进行索引,它们仍然可能使用其他类型的数据结构或算法来实现高效的查询性能。
此外,随着数据库技术的不断发展,新的索引结构和算法也在不断涌现,因此不能一概而论所有数据库系统都不使用B树进行索引。
在选择数据库系统时,了解其索引机制以及它如何支持特定的查询模式和数据访问需求是非常重要的。不同的数据库系统适用于不同的应用场景和工作负载,因此需要根据实际情况进行选择。
六、总结
B树作为一种高效的数据结构,在处理大量数据时具有显著的优势。通过了解其基本概念、性质、操作以及应用场景,我们可以更好地理解和应用B树算法。随着计算机技术的不断发展,B树将在更多领域发挥重要作用。