目录
在正文开始之前,我们先来了解贝叶斯:
贝叶斯公式是由英国数学家贝叶斯提出,它的提出是为了解决后验概率问题,即:事情已经发生,要求这件事情发生的原因是由某个因素引起的概率的问题;
通俗一点讲:就是“执果寻因”的问题
这里我们相应的补充上先验问题的含义:事情还没有发生,要求这件事情发生的概率
一. 贝叶斯公式的推导
根据条件概率公式,我们可以的到
P
(
B
∣
A
)
=
P
(
A
B
)
P
(
A
)
P(B|A)=\frac{P(AB)}{P(A)}
P(B∣A)=P(A)P(AB)
那么,设
P
(
A
)
>
0
P(A)>0
P(A)>0,则会有:
P
(
A
B
)
=
P
(
A
∣
B
)
P
(
B
)
P(AB)=P(A|B)P(B)
P(AB)=P(A∣B)P(B)
由全概率公式
P
(
A
)
=
P
(
A
∣
B
1
)
P
(
B
1
)
+
P
(
A
∣
B
2
)
P
(
B
2
)
+
.
.
.
+
P
(
A
∣
B
n
)
P
(
B
n
)
P(A)=P(A|B_{1})P(B_{1})+P(A|B_{2})P(B_{2})+...+P(A|B_{n})P(B_{n})
P(A)=P(A∣B1)P(B1)+P(A∣B2)P(B2)+...+P(A∣Bn)P(Bn)
那么,当我想求
P
(
B
∣
A
)
P(B|A)
P(B∣A)发生的概率时,我可以得到:
P
(
B
∣
A
)
=
P
(
A
B
)
P
(
A
)
=
P
(
A
∣
B
)
P
(
B
)
P
(
A
∣
B
1
)
P
(
B
1
)
+
P
(
A
∣
B
2
)
P
(
B
2
)
+
.
.
.
+
P
(
A
∣
B
n
)
P
(
B
n
)
P(B|A)=\frac{P(AB)}{P(A)}=\frac{P(A|B)P(B)}{P(A|B_{1})P(B_{1})+P(A|B_{2})P(B_{2})+...+P(A|B_{n})P(B_{n})}
P(B∣A)=P(A)P(AB)=P(A∣B1)P(B1)+P(A∣B2)P(B2)+...+P(A∣Bn)P(Bn)P(A∣B)P(B)
这也就是贝叶斯公式
我们再将公式整合后,就会得到:
P
(
B
∣
A
)
=
P
(
A
B
)
P
(
A
)
=
P
(
A
∣
B
)
P
(
B
)
∑
i
=
1
n
P
(
A
∣
H
i
)
P
(
H
i
)
P(B|A)=\frac{P(AB)}{P(A)}=\frac{P(A|B)P(B)}{\sum_{i=1}^{n}P(A|H_{i})P(H_{i}) }
P(B∣A)=P(A)P(AB)=∑i=1nP(A∣Hi)P(Hi)P(A∣B)P(B)
这里补充一点:
后验概率 P ( B ∣ A ) P(B|A) P(B∣A)
先验概率 P ( A ∣ B ) P(A|B) P(A∣B)后验概率是通过先验概率求出来的
二. 朴素贝叶斯
首先,我们来聊什么是朴素?
“朴素”的贝叶斯认为:事件与事件之间是独立的
- 这里用垃圾邮件来举例是比较容易理解的:
对于一封邮件,如果想要检测是否为垃圾邮件,最简单的做法就是:统计邮件中所有的词,绘制一个词典(可以理解为是一个1维的的向量),对于出现“买”,“优惠”等垃圾邮件高频词的特征标注为1,其他特征标注为0;对于标签值,我们认为 P ( y ) = 1 P(y)=1 P(y)=1时,为垃圾邮件
这样,垃圾邮件问题抽象为数学公式,就变为:
P
(
y
=
1
∣
X
)
=
P
(
X
∣
y
=
1
)
p
(
y
=
1
)
p
(
X
)
P(y=1|X)=\frac{P(X|y=1)p(y=1)}{p(X)}
P(y=1∣X)=p(X)P(X∣y=1)p(y=1)
P
(
y
=
0
∣
X
)
=
P
(
X
∣
y
=
0
)
p
(
y
=
0
)
p
(
X
)
P(y=0|X)=\frac{P(X|y=0)p(y=0)}{p(X)}
P(y=0∣X)=p(X)P(X∣y=0)p(y=0)
请注意:
我们之所以可以将问题抽象成公式的前提是,我们认为词与词之间没有关系,是相互独立的(但事实上,“优惠”后面出现“买”这个字的概率非常高,并不是完全独立的)
所以,对于朴素用人话来讲就是:我天真的认为事件A与事件B没有关系
1. 离散的朴素贝叶斯
朴素贝叶斯导入示例

问题:若有一个输入值,他是黑皮肤,卷头发,那么他来自哪个洲?
那么我们的问题可以抽象为:
P(y=亚|(黑卷)) 或 P(y=非|(黑卷))
是个分类问题呦!!!!
首先,我们需要计算参数,即:
- 亚洲人比例
- 非洲人比例
- 亚洲黑皮肤比例
- 亚洲黄皮肤比例
- 亚洲直发比例
- 亚洲卷发比例
- …
而后,我们需要计算每个特征的条件概率:
- P(黑皮肤|亚洲)= …
- P(黑皮肤|非洲)= …
- P(黄皮肤|亚洲)= …
- P(黄皮肤|非洲)= …
- P(直发|亚洲)= …
- P(直发|非洲)= …
- P(卷发|亚洲)= …
- P(卷发|非洲)= …
在假设条件相互独立的前提下,对于问题我们就得到了:
P
(
非
∣
黑卷
)
=
P
(
黑皮肤
∣
非洲
)
P
(
卷发
∣
非洲
)
p
(
非洲
)
p
(
黑卷
)
P(非|黑卷)=\frac{P(黑皮肤|非洲)P(卷发|非洲)p(非洲)}{p(黑卷)}
P(非∣黑卷)=p(黑卷)P(黑皮肤∣非洲)P(卷发∣非洲)p(非洲)
P ( 亚 ∣ 黑卷 ) = P ( 黑皮肤 ∣ 亚洲 ) P ( 卷发 ∣ 亚洲 ) p ( 亚洲 ) p ( 黑卷 ) P(亚|黑卷)=\frac{P(黑皮肤|亚洲)P(卷发|亚洲)p(亚洲)}{p(黑卷)} P(亚∣黑卷)=p(黑卷)P(黑皮肤∣亚洲)P(卷发∣亚洲)p(亚洲)
最后通过比较概率大小,模型将预测这个人来自…
通过上述例子,我们可以将问题推广,即
P
(
y
∣
x
1
,
x
2
,
.
.
.
,
x
n
)
P(y|x_{1},x_{2},...,x_{n})
P(y∣x1,x2,...,xn)
也就是
P
(
y
∣
x
1
,
x
2
,
.
.
.
,
x
n
)
=
p
(
y
)
P
(
x
1
,
x
2
,
.
.
.
,
x
n
∣
y
)
P
(
x
1
,
x
2
,
.
.
.
,
x
n
)
P(y|x_{1},x_{2},...,x_{n})=\frac{p(y)P(x_{1},x_{2},...,x_{n}|y)}{P(x_{1},x_{2},...,x_{n})}
P(y∣x1,x2,...,xn)=P(x1,x2,...,xn)p(y)P(x1,x2,...,xn∣y)
在朴素的条件下,我们可以将式子化简为
P
(
y
∣
x
1
,
x
2
,
.
.
.
,
x
n
)
=
p
(
y
)
∏
i
=
1
n
P
(
x
n
∣
y
)
P
(
x
1
,
x
2
,
.
.
.
,
x
n
)
P(y|x_{1},x_{2},...,x_{n})=\frac{p(y)\prod_{i=1}^{n} P(x_{n}|y)}{P(x_{1},x_{2},...,x_{n})}
P(y∣x1,x2,...,xn)=P(x1,x2,...,xn)p(y)∏i=1nP(xn∣y)
其中
P
(
x
1
,
x
2
,
.
.
.
,
x
n
)
P(x_{1},x_{2},...,x_{n})
P(x1,x2,...,xn)为常数,因此
P
(
y
∣
x
1
,
x
2
,
.
.
.
,
x
n
)
∝
p
(
y
)
∏
i
=
1
n
P
(
x
n
∣
y
)
P(y|x_{1},x_{2},...,x_{n})\propto p(y)\prod_{i=1}^{n} P(x_{n}|y)
P(y∣x1,x2,...,xn)∝p(y)i=1∏nP(xn∣y)
所以,我们的计算目标就变成了:
y
^
=
a
r
g
max
y
P
(
y
)
∏
i
=
1
n
P
(
x
n
∣
y
)
\hat{y} =arg \max_{y} P(y)\prod_{i=1}^{n} P(x_{n}|y)
y^=argymaxP(y)i=1∏nP(xn∣y)
即:求 P ( y ) ∏ i = 1 n P ( x n ∣ y ) P(y)\prod_{i=1}^{n} P(x_{n}|y) P(y)∏i=1nP(xn∣y)取最大值时,y的取值
其中y的取值在实际中不一定只有两个(亚洲,非洲),所以朴素贝叶斯算法自身就可以做多分类的,而不需要使用OVR或者OVO的方法
离散的朴素贝叶斯训练
朴素贝叶斯的准备过程:
- 构建模型:算出所有的先验概率
朴素贝叶斯的训练过程:
- 计算 p ( y i ) , p ( x j ∣ y i ) p(y_{i}),p(x_{j}|y_{i}) p(yi),p(xj∣yi)
朴素贝叶斯的应用过程:
- 以 p ( x ∣ y i ) p ( y i ) p(x|y_{i})p(y_{i}) p(x∣yi)p(yi)最大项作为x属性的类别
【注意:朴素贝叶斯没有梯度下降过程,只是在计算先验概率】
2. 连续的朴素贝叶斯
对于连续的特征属性
x
i
x_{i}
xi,我们引入密度概率,即高斯朴素贝叶斯:当特征属性为连续值时,分布服从高斯分布,在计算
P
(
x
∣
y
)
P(x|y)
P(x∣y)的时候,可以直接使用高斯分布的概率密度公式:
g
(
x
,
η
,
σ
)
=
1
2
π
σ
e
−
(
x
−
η
)
2
2
σ
2
g(x,\eta ,\sigma )=\frac{1}{\sqrt{2\pi }\sigma} e^{-\frac{(x-\eta )^{2}}{2\sigma ^{2}} }
g(x,η,σ)=2πσ1e−2σ2(x−η)2
P
(
x
i
∣
y
k
)
=
g
(
x
i
,
η
i
,
y
k
,
σ
i
,
y
k
)
P(x_{i}|y_{k})=g(x_{i},\eta _{i,y_{k}},\sigma _{i,y_{k}})
P(xi∣yk)=g(xi,ηi,yk,σi,yk)
假设有一些连续的数据,他们的label值有1,2,3…
训练过程:
特征连续时,取label为1的数据,算 η \eta η均值, σ \sigma σ方差
特征连续时,取label为2的数据,算 η \eta η均值, σ \sigma σ方差
特征连续时,取label为3的数据,算 η \eta η均值, σ \sigma σ方差
…
3. 伯努利朴素贝叶斯
伯努利分布是二项分布的一种特殊情况,可以看作是只进行一次实验的二项分布
-
二项分布是一种离散分布,即标签值为1或0
-
如果接收到了除了1和0以外的数据作为参数,可以通过BernoulliNB把输入数据二元化(取决于binarize 参数设置)
当特征属性服从伯努利分布时,公式为:
P
(
x
k
∣
y
)
=
p
(
1
∣
y
)
x
k
∗
(
1
−
p
(
1
∣
y
)
)
1
−
x
k
P(x_{k}|y)=p(1|y)^{x_{k}}\ast (1-p(1|y))^{1-x_{k}}
P(xk∣y)=p(1∣y)xk∗(1−p(1∣y))1−xk
4. 多项式朴素贝叶斯
在特征服从多项分布时(即特征离散,比如:非洲人、亚洲人的例子),对于朴素贝叶斯而言,我们的预测结果是否准确完全取决于我们的样本是否全面;
当样本存在数据小或是不全面的情况下(比如:未统计到亚洲存在黑皮肤),我们可以用平滑解决:
平滑的主要作用是克服条件概率为0的问题
4.1 Laplace平滑
p
(
y
k
)
=
N
y
k
+
α
N
+
k
∗
α
p(y_{k})=\frac{N_{y_{k}}+\alpha }{N+k\ast \alpha }
p(yk)=N+k∗αNyk+α
p
(
x
i
∣
y
k
)
=
N
y
k
,
x
i
+
α
N
y
k
,
x
i
+
n
i
∗
α
p(x_{i}|y_{k})=\frac{N_{y_{k},x_{i}}+\alpha }{N_{y_{k},x_{i}}+n_{i}\ast \alpha }
p(xi∣yk)=Nyk,xi+ni∗αNyk,xi+α
其中 α = 1 α=1 α=1
4.2 Lidstone平滑
p
(
y
k
)
=
N
y
k
+
α
N
+
k
∗
α
p(y_{k})=\frac{N_{y_{k}}+\alpha }{N+k\ast \alpha }
p(yk)=N+k∗αNyk+α
p
(
x
i
∣
y
k
)
=
N
y
k
,
x
i
+
α
N
y
k
,
x
i
+
n
i
∗
α
p(x_{i}|y_{k})=\frac{N_{y_{k},x_{i}}+\alpha }{N_{y_{k},x_{i}}+n_{i}\ast \alpha }
p(xi∣yk)=Nyk,xi+ni∗αNyk,xi+α
其中 0 < α < 1 0<α<1 0<α<1
三. 概率图模型
上面我们讨论了,当事件与事件相互独立时,朴素贝叶斯多分类任务的思想与算法;但事实是,事件与事件之间并不是完全独立的,比如:垃圾邮件中“优惠”后通常接的是“买”;machine learning中的learning是动名词而不是动词等等
诸如此类的例子,我们都可以将他们归为概率图模型,即:一种用于学习这些带有依赖的模型的强大框架
1. 贝叶斯网络(Bayesian Network)
当多个特征属性之间存在着某种相关关系的时候,朴素贝叶斯算法就无法解决问题了;而贝叶斯网络却是解决这类应用场景的一个非常好的算法
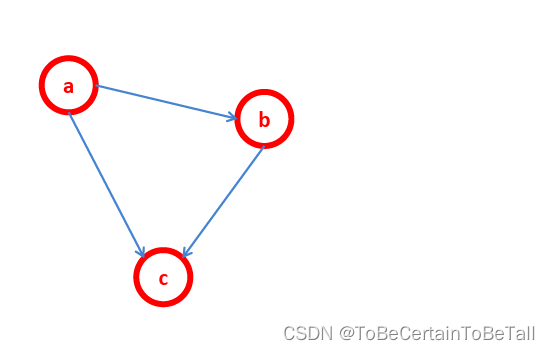
针对上面这个图,我们来做一些概念解释:
贝叶斯网络,即:把研究系统中涉及到的随机变量,根据是否条件独立绘制在一个有向图中,就形成了贝叶斯网络
贝叶斯网络又称有向无环图模型
节点表示随机变量,可以是可观察到的变量、隐变量、未知参数等等
接两个节点之间的箭头表式两个随机变量之间的因果关系,即这两个随机变量之间非条件独立
贝叶斯网络的关键方法是图模型
针对上面这幅图,我们可以得到公式
P
(
a
,
b
,
c
)
=
P
(
a
)
P
(
b
∣
a
)
P
(
c
∣
a
,
b
)
P(a,b,c)=P(a)P(b|a)P(c|a,b)
P(a,b,c)=P(a)P(b∣a)P(c∣a,b)
1.1 全连接贝叶斯网络
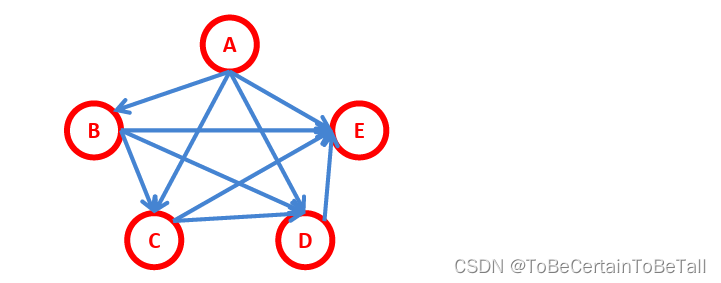
网络拓扑图全连接时,我们可以得到公式
P
(
A
,
B
,
C
,
D
,
E
)
=
P
(
A
)
P
(
B
∣
A
)
P
(
C
∣
A
,
B
)
P
(
D
∣
A
,
B
,
C
)
P
(
E
∣
A
,
B
,
C
,
D
)
P(A,B,C,D,E)=P(A)P(B|A)P(C|A,B)P(D|A,B,C)P(E|A,B,C,D)
P(A,B,C,D,E)=P(A)P(B∣A)P(C∣A,B)P(D∣A,B,C)P(E∣A,B,C,D)
进一步抽象,我们就可以得到数学关系:
P
(
x
1
,
x
2
,
.
.
.
,
x
n
)
=
∏
i
=
2
n
P
(
x
n
∣
x
1
,
x
2
,
.
.
.
,
x
n
−
1
)
P
(
x
2
∣
x
1
)
P
(
x
1
)
P(x_{1},x_{2},...,x_{n})=\prod_{i=2}^{n} P(x_{n}|x_{1},x_{2},...,x_{n-1})P(x_{2}|x_{1})P(x_{1})
P(x1,x2,...,xn)=i=2∏nP(xn∣x1,x2,...,xn−1)P(x2∣x1)P(x1)
1.2 “正常”贝叶斯网络

P
(
x
1
,
x
2
,
x
3
,
x
4
,
x
5
,
x
6
,
x
7
)
=
P
(
x
1
)
P
(
x
2
)
P
(
x
3
)
P
(
x
4
∣
x
1
,
x
2
,
x
3
)
P
(
x
5
∣
x
1
,
x
3
)
P
(
x
6
∣
x
4
)
P
(
x
7
∣
x
4
,
x
5
)
P(x_{1},x_{2},x_{3},x_{4},x_{5},x_{6},x_{7})=P(x_{1})P(x_{2})P(x_{3})P(x_{4}|x_{1},x_{2},x_{3})P(x_{5}|x_{1},x_{3})P(x_{6}|x_{4})P(x_{7}|x_{4},x_{5})
P(x1,x2,x3,x4,x5,x6,x7)=P(x1)P(x2)P(x3)P(x4∣x1,x2,x3)P(x5∣x1,x3)P(x6∣x4)P(x7∣x4,x5)
2. 隐马尔可夫模型(HiddenMarkovModel)
隐马尔科夫模型是一类基于概率统计的模型,是一种结构最简单的动态贝叶斯网,也是有向图模型
在时序数据建模,例如:语音识别、文字识别、自然语言处理等领域广泛应用
-
马尔可夫性质:
随机过程中某一状态 S t S_{t} St发生的概率,只与它的前一个状态有关,而与更前的所有状态无关 -
若某一随机过程满足马尔科夫性质,则称这一过程为马尔科夫过程,或称马尔科夫链
然而现实中,许多现象并不符合这一性质,但是我们可以假设某个事件具有马尔科夫性质,这个性质为很多无章可循的问题提供了一种解法
P ( S t ∣ S t − 1 , S t − 2 , . . , S t − n ) = P ( S t ∣ S t − 1 ) P(S_{t}|S_{t-1},S_{t-2},..,S_{t-n})=P(S_{t}|S_{t-1}) P(St∣St−1,St−2,..,St−n)=P(St∣St−1)
2.1 马尔科夫过程
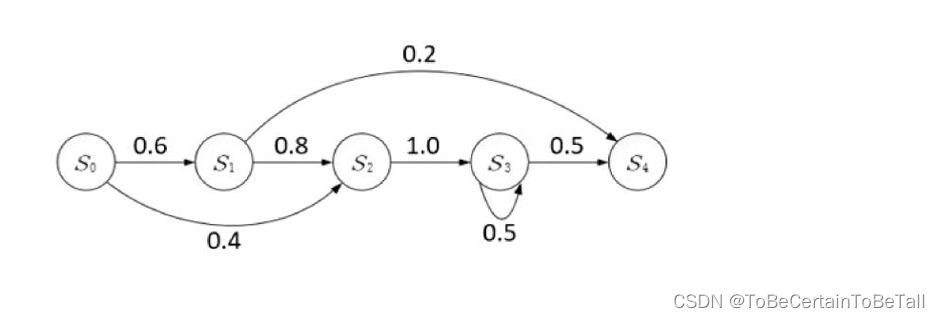
中每一个节点代表相应时刻的状态
有向箭头代表了可能的状态转移,值表示状态转移概率
2.2 隐马尔科夫过程
在一个随机过程中,马尔科夫链虽然无法直接观测到,但可以观测到每个状态的输出结果。这个输出结果只与状态有关,并且是可观测到的。这种过程被称为隐马尔科夫过程,或者称为隐马尔科夫模型。
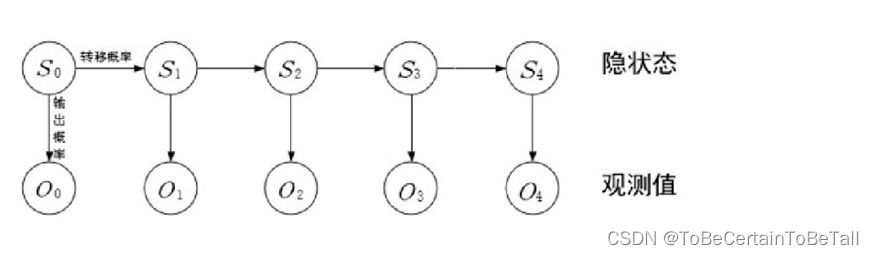
隐马尔科夫模型中,马尔科夫链指的是隐状态S0,S1,…,St 序列
感谢阅读🌼
如果喜欢这篇文章,记得点赞👍和转发🔄哦!
有任何想法或问题,欢迎留言交流💬,我们下次见!
本文相关代码存放位置
【代码实现】
祝愉快🌟!