无约束条件的最优控制问题

设函数 $x(t)$ 在 $[t_0,t_f]$ 区间上连续可到，考虑 Lagrange型性能指标函数 $J[x(t)]={\int }_{t_0}^{t_f}L[x(t),\dot{x}(t),t]dt$

性能指标变分

设宗量函数 $x(t)$, $\dot{x}(t)$ 在极值曲线 $x^{\ast }(t)$, ${\dot{x}}^{\ast }(t)$ 附近发生微小变分 $\delta x(t)$, $\delta \dot{x}(t)$, 即
$$x(t)=x^{\ast }(t)+\delta x(t),\text{\hspace{1em}(4)}$$$$\dot{x}(t)={\dot{x}}^{\ast }(t)+\delta \dot{x}(t),\text{\hspace{1em}(5)}$$则泛函 $J[x(t)]$ 的增量 $\Delta J[x(t)]$ 可表示为
Δ J [ x ( t ) ] = ∫ t 0 t f { L [ x ( t ) + δ x ( t ) , x ˙ ( t ) + δ x ˙ ( t ) , t ] − L [ x ( t ) , x ˙ ( t ) , t ] } d t = ∫ t 0 t f { ∂ L ∂ x δ x + ∂ L ∂ x ˙ δ x ˙ + o [ ( δ x ) 2 , ( δ x ˙ ) 2 ] } d t \begin{aligned} \Delta J[x(t)]&=\displaystyle\int_{t_0}^{t_f}\{L[x(t)+\delta x(t), \dot{x}(t)+\delta \dot{x}(t), t]-L[x(t), \dot{x}(t),t]\}dt\\ &=\displaystyle\int_{t_0}^{t_f}\{\frac{\partial L}{\partial x}\delta x+\frac{\partial L}{\partial \dot{x}}\delta \dot{x}+o[(\delta x)^2, (\delta \dot{x})^2]\}dt \end{aligned} ΔJ[x(t)]​=∫t0​tf​​{L[x(t)+δx(t),x˙(t)+δx˙(t),t]−L[x(t),x˙(t),t]}dt=∫t0​tf​​{∂x∂L​δx+∂x˙∂L​δx˙+o[(δx)2,(δx˙)2]}dt​其中 $$\begin{array}{r}{\int }_{t_0}^{t_f}\frac{\partial L}{\partial \dot{x}}\delta \dot{x}dt=\frac{\partial L}{\partial \dot{x}}\delta x{|}_{t_0}^{t_f}-{\int }_{t_0}^{t_f}\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})\delta xdt\end{array},$$所以$$\delta J={\int }_{t_0}^{t_f}(\frac{\partial L}{\partial x}-\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}}))\delta xdt+\frac{\partial L}{\partial \dot{x}}\delta x{|}_{t_0}^{t_f}.\text{\hspace{1em}(6)}$$由泛函极值的必要条件可得，若泛函$J[x(t)]$ 取得极值，则有$\delta J=0$, 根据（6）式，我们分如下两种情况进行分析。

1. 终端状态固定

此时初始状态 $x(t_0)=x_0$, $x(t_f)=x_f$。则关于初始条件 $x(t_0)$, $x(t_f)$ 的宗量函数 $x(t)$ 在初始状态以及终端状态的变分满足 $\delta x(t_0)=\delta x(t_f)=0$, 所以 （6）式中 $$\frac{\partial L}{\partial \dot{x}}\delta x{|}_{t_0}^{t_f}=(\frac{\partial L}{\partial \dot{x}}{)}_{t=t_f}\delta x(t_f)-(\frac{\partial L}{\partial \dot{x}}{)}_{t=t_0}\delta x(t_0)=0.\text{\hspace{1em}(7)}$$所以在此情况下若要$\delta J=0$，则有
$$\frac{\partial L}{\partial x}-\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})=0,\text{\hspace{1em}(8)}$$上式公式 (8) 称为欧拉-拉格朗日方程。

2. 终端状态不固定

此时初始条件与终端条件可发生变化，则关于初始条件 $x(t_0)$, $x(t_f)$ 的宗量函数 $x(t)$ 在初始状态以及终端状态的变分不再满足 $\delta x(t_0)=\delta x(t_f)=0$, 即 $\delta x(t_0)\ne 0,\delta x(t_f)\ne 0.$ 此时若要求公式 (6) 等于0，则需要求
$$(\frac{\partial L}{\partial \dot{x}}{)}_{t=t_f}\delta x(t_f)=0,\text{\hspace{1em}(9)}$$$$(\frac{\partial L}{\partial \dot{x}}{)}_{t=t_0}\delta x(t_0)=0,\text{\hspace{1em}(10)}$$由 $\delta x$ 的任意性，(9), (10) 等价于$$(\frac{\partial L}{\partial \dot{x}}{)}_{t=t_f}=0,\text{\hspace{1em}(11)}$$$$(\frac{\partial L}{\partial \dot{x}}{)}_{t=t_0}=0.\text{\hspace{1em}(12)}$$公式(11), (12)称为横截条件。
总结：求解无约束条件的泛函极值问题时，若给定了边界条件，则直接应用边界条件，若始端或终端状态的条件未给出，则需要使用始端或终端的横截条件进行求解。求解条件如下表所示：

例题

• 初始与终端状态固定
  求通过点 $(0,0)$, $(1,1)$ 且使 $$J={\int }_0^1(x^2+{\dot{x}}^2)dt$$取极值的最优轨迹。
  解：此处 $L(x(t),\dot{x}(t),t)=x^2+{\dot{x}}^2$, 性能指标函数相应的欧拉-拉格朗日方程为$$\frac{\partial L}{\partial x}-\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})=0.$$则有$$2x-2\frac{d}{dt}(\dot{x})=0,$$ 即 $$x-\ddot{x}=0.$$ 故求得基解为 $e^t$, $e^{-t}$, 则最优轨迹的通解可表示为 $$x(t)=c_1{e}^t+c_2{e}^{-t},\text{\hspace{1em}(13)}$$ 其中 $c_1$ 和 $c_2$ 都为常数。
  将初始条件 $x(0)=0$ 与终端条件 $x(1)=1$ 代入方程 (13) 可得：$$c_1=\frac{1}{e-e^{-1}},c_2=\frac{1}{e^{-1}-e},$$ 故而最优轨迹为 $$x(t)=\frac{e^t-e^{-t}}{e-e^{-1}}.$$
• 终端状态不固定
  求使得性能指标$$J={\int }_0^1({\dot{x}}^2+{\dot{x}}^3)dt$$ 取极值的轨迹 $x^{\ast }(t)$, 并要求 $x^{\ast }(0)=0$, 但对 $x^{\ast }(1)$ 没有限制。
  解： 此处始端状态给定，终端状态未给定，所以需要用到始端状态相关的边界条件，终端状态相关的横截条件。这里 $L(x(t),\dot{x}(t),t)={\dot{x}}^2+{\dot{x}}^3$，该性质指标函数对应的欧拉-拉格朗日函数为$$-\frac{d}{dt}(2\dot{x}+3{\dot{x}}^2)=0,\text{\hspace{1em}(14)}$$以及横截条件$$(2\dot{x}+3{\dot{x}}^2{)}_{t=1}=0.\text{\hspace{1em}(15)}$$由方程 (14) 可知，$2\dot{x}+3{\dot{x}}^2=常数$，则可知 $x^{\ast }(t)$ 为关于 $t$ 的一次函数，设 $x^{\ast }(t)=at+b$, 则由 $x^{\ast }(0)=0$ 可知 $b=0$。由方程(15)可知 $$2a+3a^2=0,\text{\hspace{1em}(16)}$$解得 $a=0$ 或 $a=-\frac{2}{3}$，所以最优轨迹 $x^{\ast }(t)$ 可表示为：
  (i) 若 $a=0$，则 $x^{\ast }(t)=0$;
  (ii) 若 $a=-\frac{2}{3}$，则 $x^{\ast }(t)=-\frac{2}{3}t$.

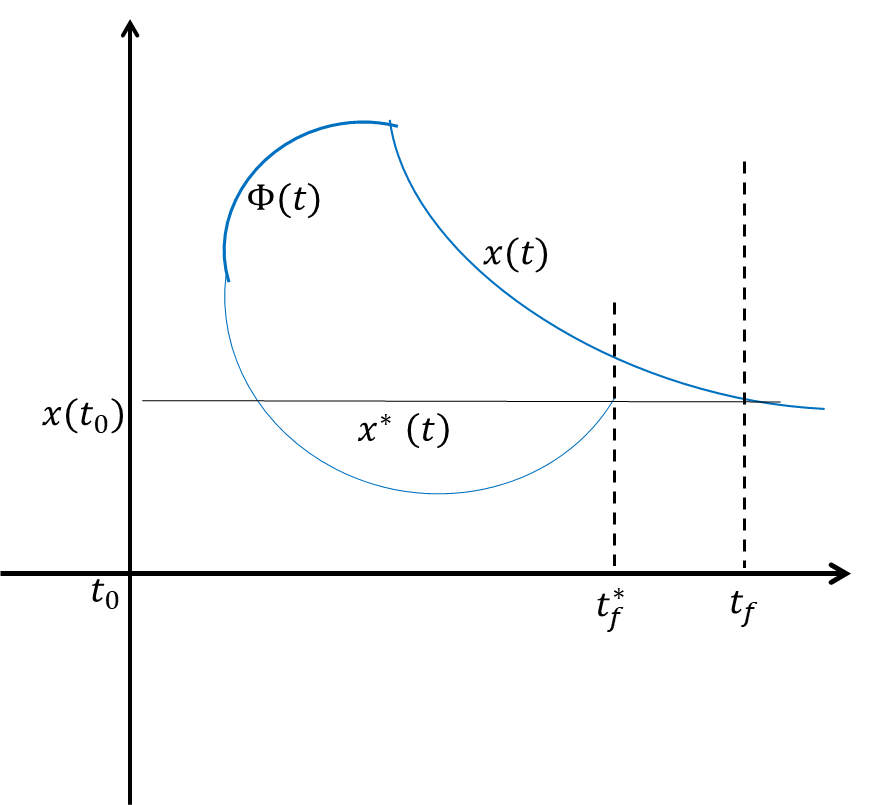
终端时刻不确定的性能指标变分

此时性能指标函数 $J[x(t)]={\int }_{t_0}^{t_f}L[x(t),\dot{x}(t),t]dt$ 类似于一个变上限的积分函数。
类似于终端时刻确定时，设宗量函数 $x(t)$, $\dot{x}(t)$ 在极值曲线 $x^{\ast }(t)$, ${\dot{x}}^{\ast }(t)$ 附近发生微小变分 $\delta \eta (t)$, $\delta \dot{\eta }(t)$, 其中 $\eta (t)$ 是一个连续可导的任意定义区间内的函数，即
$$x(t)=x^{\ast }(t)+\delta \eta (t),\text{\hspace{1em}(14)}$$
$$\dot{x}(t)={\dot{x}}^{\ast }(t)+\delta \dot{\eta }(t),\text{\hspace{1em}(15)}$$
取得状态 $x^{\ast }$ 的时刻为 $t_f^{\ast }$, 状态 $x(t)$ 对应 时刻 $t_f$, 设 $t_f=t_f^{\ast }+\delta \xi (t_f^{\ast })$
则泛函 $J[x(t)]$ 的增量 $\Delta J[x^{\ast }(t)]$ 可表示为
Δ J [ x ∗ ( t ) ] = ∂ J ∂ δ ∣ δ = 0 = ∫ t 0 t f ∗ { L [ x ( t ) , x ˙ ( t ) , t ] − L [ x ∗ ( t ) , x ˙ ∗ ( t ) , t ] } d t + L [ x ∗ ( t f ∗ ) , x ˙ ∗ ( t f ∗ ) , t f ∗ ] ξ ( t f ∗ ) = ∫ t 0 t f ∗ { ∂ L ∂ x δ η + ∂ L ∂ x ˙ δ η ˙ + o [ ( δ η ) 2 , ( δ η ˙ ) 2 ] } d t + L [ x ∗ ( t f ∗ ) , x ˙ ∗ ( t f ∗ ) , t f ∗ ] ξ ( t f ∗ ) \begin{aligned} \Delta J[x^*(t)]&=\frac{\partial J}{\partial \delta}|_{\delta=0}\\ &=\displaystyle\int_{t_0}^{t_f^*}\{L[x(t), \dot{x}(t),t]-L[x^*(t), \dot{x}^*(t),t]\}dt+L[x^*(t_f^*), \dot{x}^*(t_f^*),t_f^*]\xi(t_f^*)\\ &=\displaystyle\int_{t_0}^{t_f^*}\{\frac{\partial L}{\partial x}\delta \eta+\frac{\partial L}{\partial \dot{x}}\delta \dot{\eta}+o[(\delta \eta)^2, (\delta \dot{\eta})^2]\}dt+L[x^*(t_f^*), \dot{x}^*(t_f^*),t_f^*]\xi(t_f^*) \end{aligned} ΔJ[x∗(t)]​=∂δ∂J​∣δ=0​=∫t0​tf∗​​{L[x(t),x˙(t),t]−L[x∗(t),x˙∗(t),t]}dt+L[x∗(tf∗​),x˙∗(tf∗​),tf∗​]ξ(tf∗​)=∫t0​tf∗​​{∂x∂L​δη+∂x˙∂L​δη˙​+o[(δη)2,(δη˙​)2]}dt+L[x∗(tf∗​),x˙∗(tf∗​),tf∗​]ξ(tf∗​)​
其中
$$\begin{array}{r}{\int }_{t_0}^{t_f^{\ast }}\frac{\partial L}{\partial \dot{x}}\delta \dot{\eta }dt=\frac{\partial L}{\partial \dot{x}}\delta \eta {|}_{t_0}^{t_f^{\ast }}-{\int }_{t_0}^{t_f^{\ast }}\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})\delta \eta dt\end{array}.$$
因此 $\delta J$ 取得极值的必要条件为：
（1）欧拉-拉格朗日方程：
$$\frac{\partial L}{\partial x}-\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}})=0,$$
(2) 横截条件：
$$\eta (t)\frac{\partial L}{\partial \dot{x}}{|}_{t_0}^{t_f^{\ast }}+L[x^{\ast }(t_f^{\ast }),{\dot{x}}^{\ast }(t_f^{\ast }),t_f^{\ast }]\xi (t_f^{\ast })=0.$$ 通常，无论边界情况如何，泛函极值都必须满足欧拉-拉格朗日方程，只是在不同的情况下会出现不同的边界情况，以下我们分情况进行讨论。

1. 给定始端状态与终端状态
   
   此时 $x(t_0)=x_0$, $\eta (t_0)=0$, $\eta (t_f^{\ast })=0$, $x(t_f)=x_f$, 则可得边界条件与横截条件为
   $$x(t_0)=x_0,x(t_f)=x_f,L[x(t_f^{\ast }),\dot{x}(t_f^{\ast }),t_f^{\ast }]=0.$$
2. 始端状态给定，终端状态自由
   此时 $x(t_0)=x_0$, $\eta (t_0)=0$, $\eta (t_f^{\ast })\ne 0$, 则可得边界条件与横截条件为
   $$x(t_0)=x_0,\frac{\partial L}{\partial \dot{x}}{|}_{t_f^{\ast }}=0,L[x(t_f^{\ast }),\dot{x}(t_f^{\ast }),t_f^{\ast }]=0.$$
3. 始端状态给定，终端状态有约束（要求 $x(t_f)=C(t_f)$）
   
   $x(t)=x^{\ast }(t)+\epsilon \eta (t)$, $t_f=t_f^{\ast }+\epsilon \xi (t_f^{\ast })$则有
   $$\begin{array}{rl}C(t_f)& =x(t_f)\\ & =x^{\ast }(t_f)+\epsilon \eta (t_f)\\ & =x(t_f^{\ast }+\epsilon \xi (t_f^{\ast }))\\ & =x^{\ast }(t_f^{\ast }+\epsilon \xi (t_f^{\ast }))+\epsilon \eta (t_f^{\ast }+\epsilon \xi (t_f^{\ast }))\\ & =C(t_f^{\ast }+\epsilon \xi (t_f^{\ast }))\end{array}$$
   上式在 $\epsilon =0$ 处取求导可得
   $$\begin{array}{rl}& \eta (t_f^{\ast }+\epsilon \xi (t_f^{\ast })){|}_{\epsilon =0}\\ & =\frac{C(t_f^{\ast }+\epsilon \xi (t_f^{\ast }))-x^{\ast }(t_f^{\ast }+\epsilon \xi (t_f^{\ast }))}{\epsilon }{|}_{\epsilon =0}\\ & =(\dot{C}(t_f^{\ast })-{\dot{x}}^{\ast }(t_f^{\ast }))\xi (t_f^{\ast })\\ & =\eta (t_f^{\ast })\end{array}$$则可得边界条件与横截条件为
   $$\{\begin{array}{l}x(t_0)=x_0,\\ x(t_f)=C(t_f),\\ (\dot{C}(t_f^{\ast })-{\dot{x}}^{\ast }(t_f^{\ast }))\frac{\partial L}{\partial \dot{x}}{|}_{t_f^{\ast }}+L[x^{\ast }(t_f^{\ast }),{\dot{x}}^{\ast }(t_f^{\ast }),t_f^{\ast }]=0.\end{array}$$
4. 始端状态有约束（要求 $x(t_0)=\Phi (t_0)$），终端状态固定
   

$x(t)=x^{\ast }(t)+\epsilon \eta (t)$, $t_0=t_0^{\ast }+\epsilon \xi (t_0^{\ast })$则有
$$\begin{array}{rl}\Phi (t_0)& =x(t_0)\\ & =x^{\ast }(t_0)+\epsilon \eta (t_0)\\ & =x(t_0^{\ast }+\epsilon \xi (t_0^{\ast }))\\ & =x^{\ast }(t_0^{\ast }+\epsilon \xi (t_0^{\ast }))+\epsilon \eta (t_0^{\ast }+\epsilon \xi (t_0^{\ast }))\\ & =C(t_0^{\ast }+\epsilon \xi (t_0^{\ast }))\end{array}$$
上式在 $\epsilon =0$ 处取求导可得
$$\begin{array}{rl}& \eta (t_0^{\ast }+\epsilon \xi (t_0^{\ast })){|}_{\epsilon =0}\\ & =\frac{C(t_0^{\ast }+\epsilon \xi (t_0^{\ast }))-x^{\ast }(t_0^{\ast }+\epsilon \xi (t_0^{\ast }))}{\epsilon }{|}_{\epsilon =0}\\ & =(\dot{C}(t_0^{\ast })-{\dot{x}}^{\ast }(t_0^{\ast }))\xi (t_0^{\ast })\\ & =\eta (t_0^{\ast })\end{array}$$则可得边界条件与横截条件为
$$\{\begin{array}{l}x(t_f)=x_f,\\ x(t_0)=\Phi (t_f),\\ (\dot{\Phi }(t_0^{\ast })-{\dot{x}}^{\ast }(t_0^{\ast }))\frac{\partial L}{\partial \dot{x}}{|}_{t_0^{\ast }}+L[x^{\ast }(t_0^{\ast }),{\dot{x}}^{\ast }(t_0^{\ast }),t_0^{\ast }]=0.\end{array}$$
总结：在终端时刻不确定的条件下，求解无约束条件的泛函极值问题时，若给定了边界条件，则直接应用边界条件，若始端或终端状态的条件未给出，则需要使用始端或终端的横截条件进行求解。求解条件如下表所示：

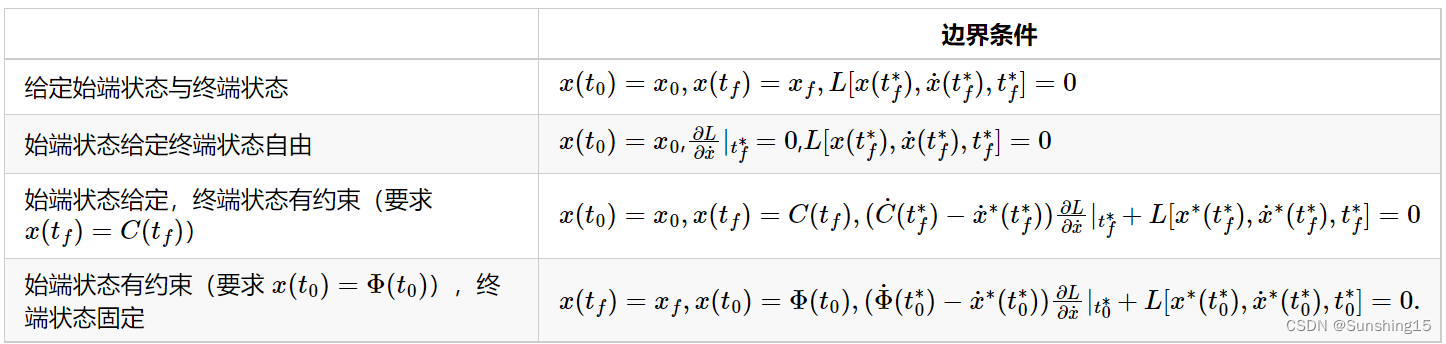
例题

求使性能指标 $$J={\int }_{t_0}^{t_f}(1+{\dot{x}}^2{)}^{\frac{1}{2}}dt$$ 为极小时的最优轨线 $x^{\ast }(t)$。设 $x(0)=1,x(t_f)=C(t_f),C(t_f)=2-t$, $t_f$ 未给定。
解题思路 本题为无约束条件，始端状态时刻给定，终端状态有约束，终端时刻自由的泛函极值问题。
令 $L(x,\dot{x},t)=(1+{\dot{x}}^2{)}^{\frac{1}{2}}$。则可得欧拉-拉格朗日方程为$$\frac{\partial L}{\partial x}-\frac{d}{dt}\frac{\partial L}{\partial \dot{x}}=0,\text{\hspace{1em}(e1)}$$可得$$-\frac{d}{dt}(\frac{\dot{x}}{(1+{\dot{x}}^2{)}^{\frac{1}{2}}})=0,\text{\hspace{1em}(e2)}$$则有$$\frac{\dot{x}}{(1+{\dot{x}}^2{)}^{\frac{1}{2}}}=c,\text{\hspace{1em}(e3)}$$得$${\dot{x}}^2=\frac{c^2}{1-c^2},c^2\ne 1.\text{\hspace{1em}(e4)}$$即 $\dot{x}$ 为常数，进而可知 $x(t)$ 为一次函数形式，设 $$x(t)=at+b,\text{\hspace{1em}(e5)}$$代入初始条件 $x(0)=1$ 可得 $b=1$。由横截条件$$(\dot{c}(t_f)-\dot{x}(t_f))\frac{\partial L}{\partial \dot{x}}|t_f=t_f^{\ast }+L(x(t_f),\dot{x}(t_f),t_f)=0,$$可得$$(-1-a)[\frac{a}{(1+a^2{)}^{\frac{1}{2}}}]+(1+a^2{)}^{\frac{1}{2}}=0,$$整理可得$$a(a-1)(a+2)=0,\text{\hspace{1em}(e6)}$$由（e6）可知 $a=0$, 或 $a=1$ 或 $a=-1$. 经验算可知 $a=-1$ 时，不满足终端约束 $x(t_f)=c(t_f)$,即会有 $-t_f+1=2-t_f$。所以$a=0$, 或 $a=1$。
（1）当 $a=0$ 时，最优轨迹为 $x(t)=1$, 代入条件 $x(t_f)=c(t_f)$，得最优时刻为 $t_f^{\ast }=1$。
（2）当$a=1$ 时，最优轨迹为 $x(t)=t+1$, 代入条件 $x(t_f)=c(t_f)$，得最优时刻为 $t_f^{\ast }=\frac{1}{2}$。