Problem - C - Codeforces
通用领域
医学
计算机
金融经济
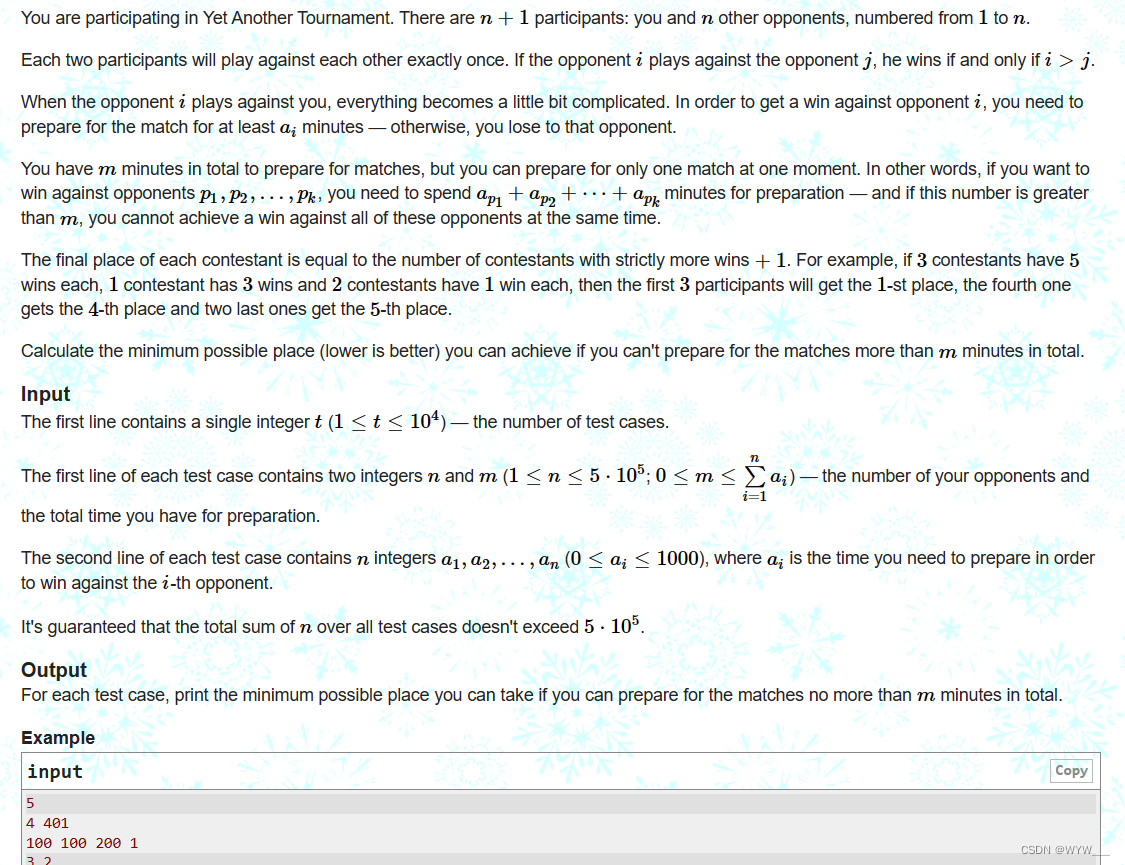
你正在参加另一场比赛。有n+1个参与者:你和其他n个对手,编号从1到n。
每两名参与者将相互竞争一次。如果对手i和对手j比赛,他获胜当且仅当i>j。
当我的对手和你对弈时,一切都变得有点复杂。为了赢下对手i,你需要准备至少ai分钟的比赛——否则,你会输给对手。
你总共有m分钟的时间准备比赛,但你一次只能准备一场比赛。换句话说,如果你想赢下对手p1,p2,…,pk,你需要花ap1+ap2+⋯⋯apk分钟来准备-如果这个数字大于m,你无法同时赢下所有这些对手。
每位选手的最终名次等于获胜次数加1的选手数。例如,3个选手各5胜,1个选手3胜,2个选手各1胜,则前3名获得第一名,第4名获得第四名,最后2名获得第五名。
计算如果你准备比赛的总时间不能超过m分钟,你可以达到的最小可能位置(越低越好)。
输入
第一行包含一个整数t(1≤t≤104)——测试用例的数量。
每个测试用例的第一行包含两个整数n和m(1≤n≤5⋅105;0≤m≤∑i=1nai) -你的对手数量和你准备的总时间。
每个测试用例的第二行包含n个整数a1,a2,…,an(0≤ai≤1000),其中ai是为了战胜第i个对手而需要准备的时间。
它可以保证所有测试用例的n之和不超过5⋅105。
输出
对于每个测试用例,如果你准备比赛的总时间不超过m分钟,打印出你可以参加比赛的最小地点。
例子
inputCopy
5
4 401
100 100 200 1
3 2
1 2 3
5 0
1 1 1 1 1 1
4 0
0 1 1 1
4 4
1 2 2 1
outputCopy
1
2
6
4
1
请注意
在第一个测试案例中,你可以为所有对手做准备,因此你将赢得4场比赛并获得第一名,因为你的所有对手赢得的比赛不超过3场。
在第二个测试案例中,您可以针对第二个对手进行准备并获胜。结果,你会有1胜,对手1胜1负,对手2胜1负,对手3胜3负。所以,对手3将获得第一名,其他所有参与者,包括你,获得第二名。
在第三个测试案例中,你根本没有时间准备,因此你将输掉所有游戏。因为每个对手都至少赢了1次,所以你将获得最后一名(第6名)。
在第四个测试案例中,你没有时间准备,但你仍然可以战胜第一个对手。结果是,对手1没有胜利,你1次胜利,其他所有人至少2次胜利。所以你的位置是4。
题解:
由于下标大的一定可以赢下标小的,下标1~n每个人最少赢的场数为i-1,最多赢的场数是赢了我+1
变为i,我们先假设他们都赢了我,赢得场数为i
我们应该想想把分配时间,分配给哪几个人
先不管其他因素,要想我单纯赢得场数最多,应该取需要时间最少的那几个人
我们就先对时间进行排序,
但是通过样例2发现,取第二个人是最优的(赢得场数相同的人名次是一样的)
3 2
1 2 3
所以还要考虑其他因素,假如排完后,最多前w个人的时间相加是 <= m,
那我们先考虑前w个人,如果前w个人出现他的原本编号为w + 1,由于我们是假设都赢过我的,但是这个人现在被我赢了,所以,他赢得场数变成了w,我的名次就更进一步了,
接下来我们在考虑,w 后面的人如果出现一个人原本的编号是w+1,我们看看如果我们不赢第w个人,而赢这个人是否时间足够,如果足够,我赢得场数还是w,但是就像刚才分析的,那个人赢的场数就变成了w,我的名次更进一步,
#include<iostream>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<map>
#include<cstring>
#include<cmath>
#include<stack>
#include<set>
using namespace std;
#define int long long
typedef pair<int,int> PII;
const int N = 2e5 + 10;
PII a[500005];
int n,m;
void solve()
{
cin >> n >> m;
for(int i = 1;i <= n;i++)
{
cin >> a[i].first;
a[i].second = i;
}
sort(a+1,a+1+n);
int w = 0;
for(int i = 1;i <= n;i++)
{
if(m - a[i].first >= 0)
{
m -= a[i].first;
w++;
}
else
{
break;
}
}
int f = 0;
for(int i = 1;i <= w;i++)
{
if(a[i].second == w+1)
{
f = 1;
break;
}
}
for(int i = w + 1;i <= n;i++)
{
if(a[i].second == w+1)
{
if(m - a[i].first + a[w].first >= 0)
{
f = 1;
break;
}
}
}
if(f)
w++;
cout << n - w + 1<<'\n';
}
//1 -7 1 -7
signed main(){
// ios::sync_with_stdio(false);
// cin.tie(0);
// cout.tie(0);
int t = 1;
cin >> t;
while(t--)
{
solve();
}
}
//3 3 2 2 1 0
//1 2 1 1 1 0