ps：先自我检讨...自从世界杯开始后，就一直摆烂到现在。直到打了今年的第一场cf，看见打的这么菜，真是想remake/。后面我会陆陆续续的补完前段时间没有打的比赛...
Dashboard - Educational Codeforces Round 141 (Rated for Div. 2) - Codeforces
A:构造
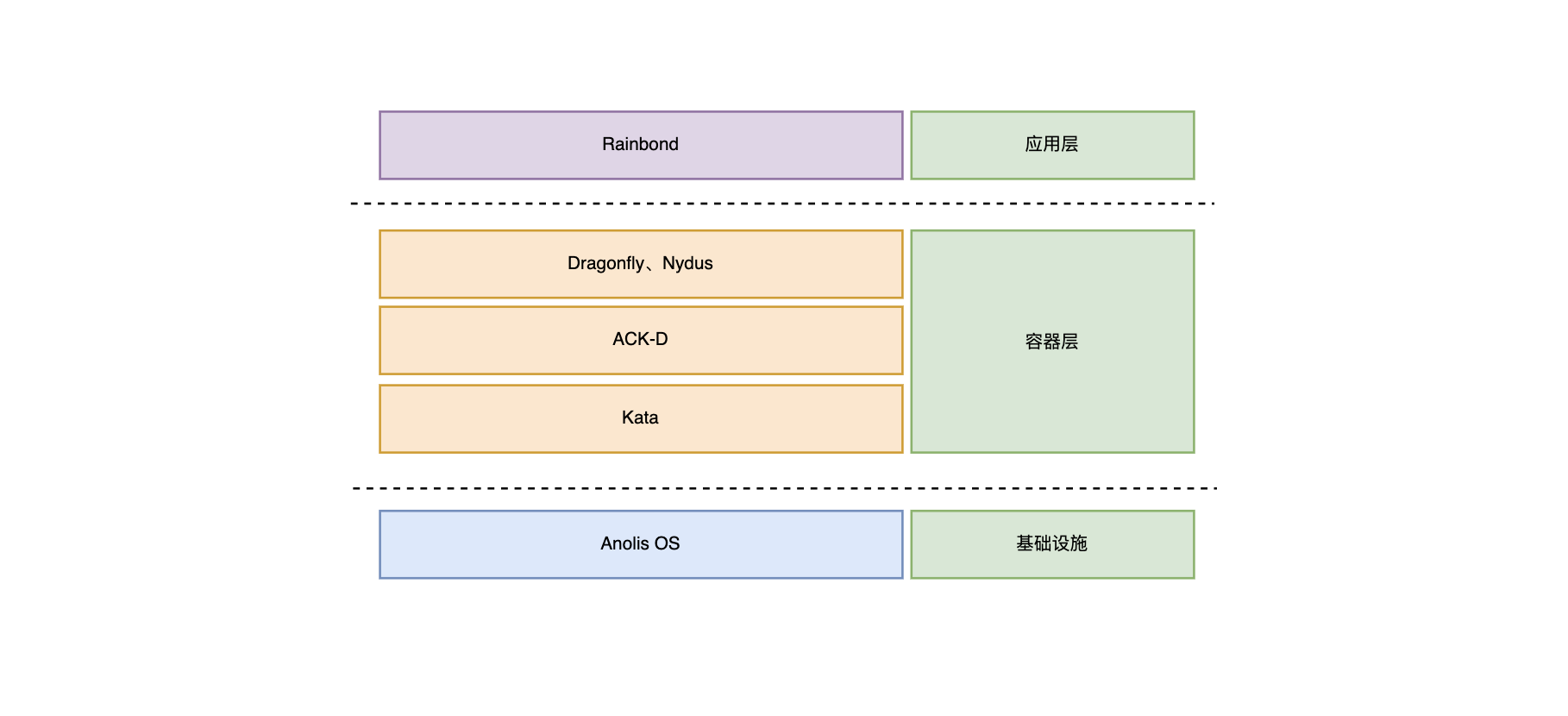
题意：给定一个长度为 n 的数组，将该数组重新排列使得数组内的每一个数都不等于其前面的所有数字之和。
方法：这里很容易想到用降序排列构造数组。因为是降序，那么前面的一段和就不可能等于后面的某一个数。然后我们用条件去判断一下这个构造数组是否可行即可。
代码：
#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=51;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}// a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%p
int a[N],b[N],sum[N];
inline void solve() {
int n;cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+1+n,greater<int>());
int i=1,j=n,l=0;
while(i<=j){
b[++l]=a[i],i++;
b[++l]=a[j],j--;
}
for(int i=1;i<=n;i++) sum[i]=sum[i-1]+b[i];
for(int i=1;i<=n;i++){
if(sum[i-1]==b[i]){
cout<<"NO\n";return;
}
}
cout<<"YES\n";
for(int i=1;i<=n;i++) cout<<b[i]<<" ";
cout<<"\n";
}
signed main(){
fast;int T;cin>>T;
while(T--) solve();
}B:构造
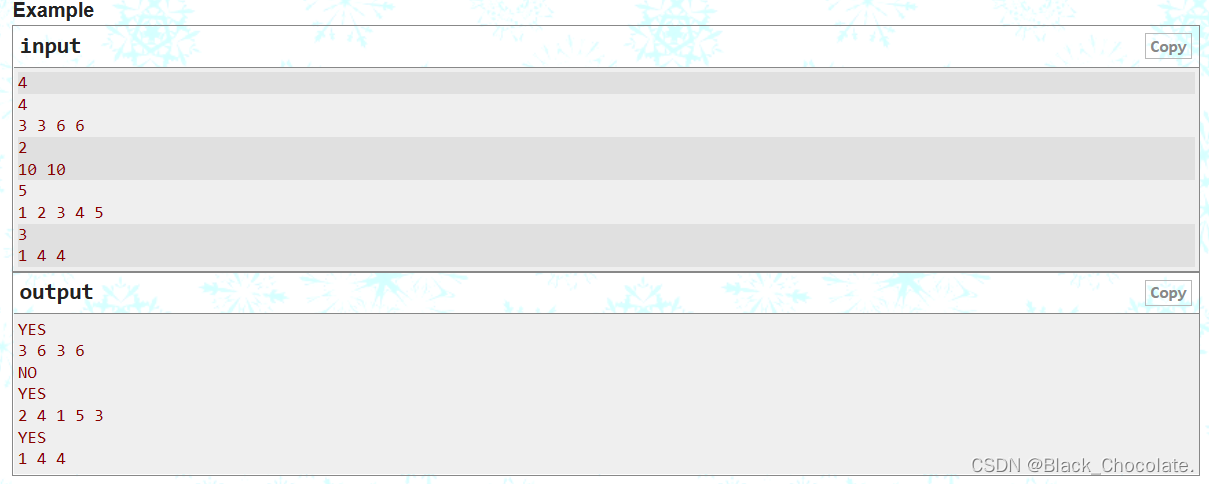
题意：请构造一个长宽为 n 的矩阵，要求矩阵内所有的数字是 [1,n^2] 的排列，且要求矩阵内每两个相邻数之间的绝对值之差的种类数量最多，输出该矩阵。
ps：一开始把题读错了...呜呜呜
方法：因为是构造，这道题很难解释的通。只能说是，如果想到了，那么会很简单。想不到就只能gg了。我们发现，只要构造一个差为[1,n-1]的蛇形矩阵即可。
简单蛇形矩阵图：
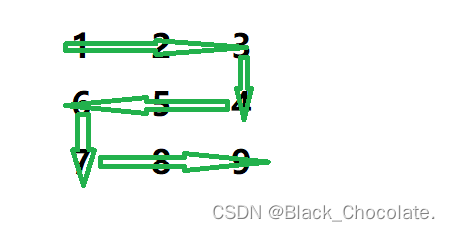
方向可自定义，但是满足蛇形的就可以
代码：各位可以通过代码找构造出矩阵的规律哦
#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e6+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}// a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%p
int a[N],b[N],sum[N],mp[51][51];
inline void solve() {
int n;cin>>n;
int l=1,r=n*n;
int cnt=0;
for(int i=1;i<=n;i++){//行
if(i&1){//奇数行
for(int j=1;j<=n;j++,cnt++){
if(cnt&1) mp[i][j]=r--;
else mp[i][j]=l++;
}
}
else{//偶数行
for(int j=n;j>=1;j--,cnt++){
if(cnt&1) mp[i][j]=r--;
else mp[i][j]=l++;
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)
cout<<mp[i][j]<<" ";
cout<<"\n";
}
}
signed main(){
fast;int T;cin>>T;
while(T--) solve();
}C:贪心（也可以二分）
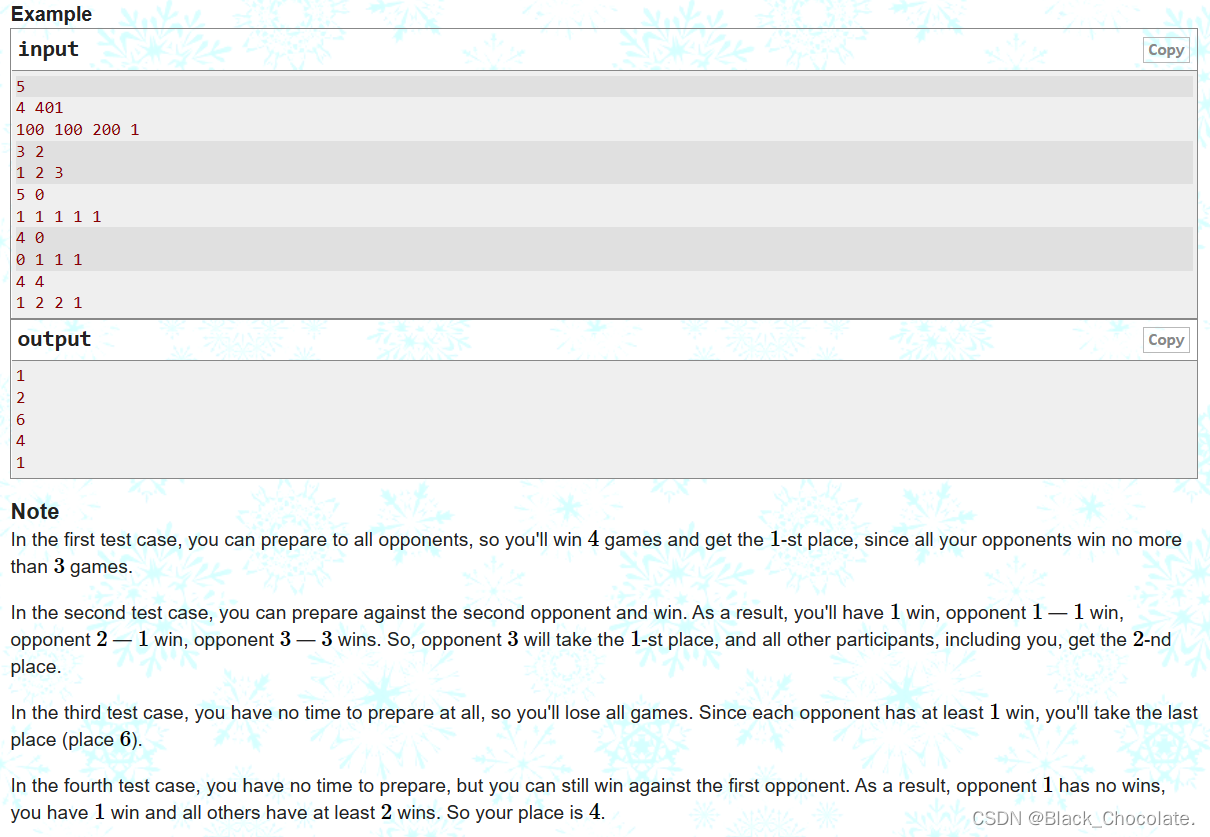题意： 有n名玩家，战斗力分别为 [1,n] ，自己也是一名玩家，一共有 n+1 名玩家。对于 n 名玩家来说， i 能击杀 j 当且仅当 i>j 。对于每一位玩家我们都有一个准备值 ai ，我们想要击败该名玩家需要花费 ai 的时间去准备。刚开始我们拥有的时间为 m ，每名玩家都和其余所有玩家进行一轮对局，最终按照胜场数量对所有玩家进行排名，求我们合理分配时间会获得的最高排名。
方法：根据题意，我们可以知道。一名玩家的胜场在[0,n-1]。假设我们自己的胜场是x，那么我们可以击败前x名玩家，如果我们想要自己的胜场是x+1，那么我们只有赢了第x+1名玩家，我们才会多得胜场。
贪心策略：在有限的时间内，尽可能击杀更多的对手。对此，我们应该先保证在胜场的情况下去贪心。我们先计算出最多能够击杀多少名玩家，然后判断这些玩家中能否包括x+1，如果包括了，我们就可以使得自己的排名上升。
计算最多胜利的场数，按照ai_i排序，然后标记所有可能被击杀的玩家。
答案：
//注意：想想排名是怎么计算的哦
#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e6+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}// a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%p
int n,m,k,a[N],b[N];
bool st[N];//记录可以击杀下标为i的对手
struct Node{
int id,v;
bool operator<(const Node&A)const{
return v<A.v;
}
}w[N];
inline void solve() {
cin>>n>>m;
memset(st,false,sizeof st);
for(int i=1;i<=n;i++){
cin>>a[i];
w[i]={i,a[i]};
}
sort(w+1,w+1+n);//按照准备值由小到大排，以获得最大击杀数
int cur=m,wins=0;//cur：当前值 wins：获胜场数
for(int i=1;i<=n;i++){
auto [id,v]=w[i];
if(cur>=v) cur-=v,wins++,st[id]=true;
else{//记录完所有能够击杀的对手后
int j=i;//在保证赢的场次下，将所有可能获胜的玩家进行标记
while(j<=n&&cur+w[i-1].v>=w[j].v) st[w[j++].id]=true;
break;
}
}
cout<<n-wins+1-st[wins+1]<<"\n";
}
signed main(){
fast;int T;cin>>T;
while(T--) solve();
}
