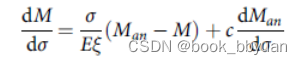用ode45解微分方程遇到的实际问题

news2024/9/28 15:30:03

最近在用ode45解微分方程数值解，试图复现论文中的图。一般来说说微分方程（组）只要按照响应的条件去撰写好对应的回调函数即可，基本没什么难度，但对于本文遇到的的这个问题，可能还需要一些技巧去实现解法，这篇文章就来说说我们其中遇到的几个问题。

一、问题提出和简单分析：

方程的条件和初值如下：

常系数和初始变量：

模型参数：Ms=1.6x10^6；a=1000；alpha=0.001；,mu0=4πx10^7 ；c=0.1；gamma1=7x10^-18；gamma1_p=-1x10^-25 ；gamma2 =-3.3x10^-30 ；gamma2_p=2.1x10^-38 ；E=2.02x10^11 ；ksi=2000 ；H=40 ；

自变量σ区间为[0,300]MPa 注意：1MPa=1×106 Pa ，代入公式计算的时候注意这一点，上面的模型参数都是在Pa的基础上赋值的。

M初始值分别为： M(0)=0 ;M(0)=10000 ;M(0)=20000;M(0)=30000;M(0)=40000;

简单的分析，这应该是一个二元一阶常系数微分方程组，只有dM和dMan需要关注，其他变量，Heff，Hsigma都是与Man有关，Man是比较关键的变量，但是Man和dMan的表达都没有直接形式，这个需要注意。Hsigma是搭桥，基本联通Heff和Hman，Heff和Man相互纠缠。

二、解决初值问题

我们在带入ode45的表达式中，初值是一个必要的参数。

题目中给了M的初始值，但是Man没有给出，这个得想办法求出来。通过观察应该是由原方程组的前三个式子组成的方程来求解。

也即解决由这三个式子在sigma=0的条件下，Man的值

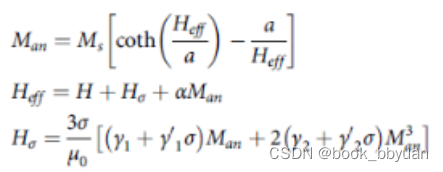
第三个式子由于sigma为零，Hsigma=0，另外Man 和Heff 这俩显然是个超越方程，估计没有解析解，我们求数值解。

我们使用fsolve解数值解，因为不知道初值，随便定了Man和Heff为1，Hsigma为0

% Man ,Heff,Hsigma 初值，sigma=0 下
[x,fval,exitflag]=fsolve(@myfun,[1 1 0]);

myfun中关键代码如下：

eq1 = Man -( Ms*(coth(Heff/a)-a/Heff));
eq2 = Heff- (H+Hsigma+alpha*Man);
eq3 = Hsigma - (3*sigma/mu0*((gamma1 + gamma1_p*sigma)*Man + 2*(gamma2 + gamma2_p*sigma)*Man*Man*Man));

F = [eq1;eq2;eq3];

结果是找不到，这说明初值没有选定，找了几个初值都不行，看来要具体分析一下Man和Heff的关系了，这边使用画图法，实际曲线来看看两者到底交叠在哪个点上，根据eq1和eq2，我们稍微变动一下，画出 Man和Heff的走势曲线

Ms = 1.6e6;
a = 1000;
H = 40;
alpha = 0.001;
Heff = [1:500];

for i = 1:length(Heff)
    
    Man1(i) =( Ms*(coth(Heff(i)/a)-a/Heff(i)));
    Man2(i) = (Heff(i)- H)/alpha;

end

plot(Heff,Man1,'r');
hold on
plot(Heff,Man2,'b');

大概交叉在Heff = 86，Man=46000，左右，【这种初值靠你随便指定手写，估计是不可能的】，好了初值问题选定，现在终于可以迈入第下一步了！, 这一步算出来的 Man的初值是 45666.419496657

二、dMan的确定

[x,y] = ode45(@(x,y)f(x,y,st),[t(1),t(end)],y0,nstep);

其中y是[M0,Man0], 在回调函数内部，大致的结构如下

 function dydt = f(x,y,st)  
    sigma = x;
    dydt = zeros(size(y));
   
    %y(1), y(2)
    %M, Man

    Man = y(2);
    
    %想办法求出来 dMan_dt

    dydt(2)= dMan_dt;       
    dydt(1) = sigma /(E*ksi) * (y(2) - y(1)) + c* dydt(2);

end

这里面的步骤很有讲究，你要先取出积分自变量x也就是t，也是sigma，另外y的值y(1) = M,y(2)=Man, 但是M的值基本用不上，sigma、Man的值要用在求dMan_dt上，算出来的dydt(2) 又要被dydt(1)用，所以写在最后面。

dMan不知道，是不是可以对前面三个式子都对sigma求导，解一个 [Man,Heff,dHsigma,dMan,dHeff,dHsigma,sigma] 这么一个五元的方程组（Man和sigma能知道），还得是数值解。这个最麻烦的就是初值，Heff的初值还好办，那些微分式子的初值很难估计。

求dMan_dsigma 非常关键。上述办法估计行不动，需要变通一下思维。经过前面的分析，Heff和Man相互嵌套，可以利用这点，

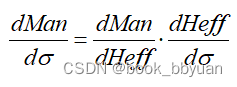dMan_dHeff, 它出来的结果基本都是Man的函数，另外Heff的微分也都是sigma和Man，这就好办了, 也就是找到了下面的这个函数关系，最重要的是Man和sigma都是已知！

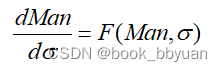
只是链式微分式子比较可怕

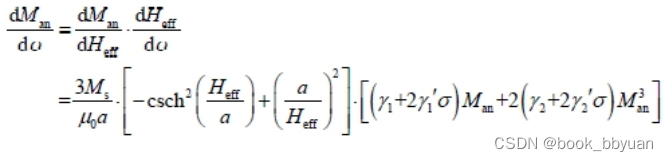
没有关系，我们交给Matlab吧

    Hsigma = (3*sigma/mu0*((gamma1 + gamma1_p*sigma)*Man + 2*(gamma2 + gamma2_p*sigma)*Man*Man*Man));
    Heff = H + Hsigma + alpha *Man;
    pp = (gamma1 + 2*gamma1_p*sigma)*Man + 2*(gamma2 + 2*gamma2_p*sigma)*Man*Man*Man;
    dMan_dt = 3*Ms/(mu0*a)*( -(csch(Heff/a))^2 + (a/Heff)^2) *pp;

至此已经解决掉这些问题了，我们最后看看图像如何；

三、心心念念的图