解法一：

根据题目的题目描述进行模拟，遇到偶数$i$将$arr[i]=prem[i/2]$,遇到奇数$i$,将$arr[i]=prem[(n-1+i)/2]$

• 时间复杂度: $O(n^2)$, 最多会循环n次
• 空间复杂度：$O(n)$

class Solution {
    public int reinitializePermutation(int n) {
        int[] prem = new int[n], arr = new int[n];
        for (int i = 0; i < n; i++) prem[i] = i;
        int i, step = 1;
        while (true) {
            for (i = 0; i < n; i++) arr[i] = i % 2 == 0 ? prem[i / 2] : prem[(n - 1 + i) / 2];
            for (i = 0; i < n && arr[i] == i; i++); 
            if (i == n) return step;
            for (i = 0; i < n; i++) prem[i] = arr[i];
            step++;
        }
    }
}

class Solution {
public:
    int reinitializePermutation(int n) { 
        vector<int> prem(n), arr(n);
        for (int i = 0; i < n; i++) prem[i] = i;
        int i, step = 1;
        while (true) {
            for (i = 0; i < n; i++) arr[i] = i % 2 == 0 ? prem[i / 2] : prem[(n - 1 + i) / 2];
            for (i = 0; i < n && arr[i] == i; i++); 
            if (i == n) return step;
            for (i = 0; i < n; i++) prem[i] = arr[i];
            step++;
        }
    }
};

解法二：模拟优化

对于解法一来说我们枚举了所有位置进行交换，但其实我们不用枚举所有位置。通过分析可以发现，所有的数交换后会构成一个环，每个环经过它长度的交换后就回会到最初的状态，那么我们求出最大的环的长度(可以发现必然是所有环的最小公倍数），经过在这个长度的交换，所有数必然回到最初的位置。

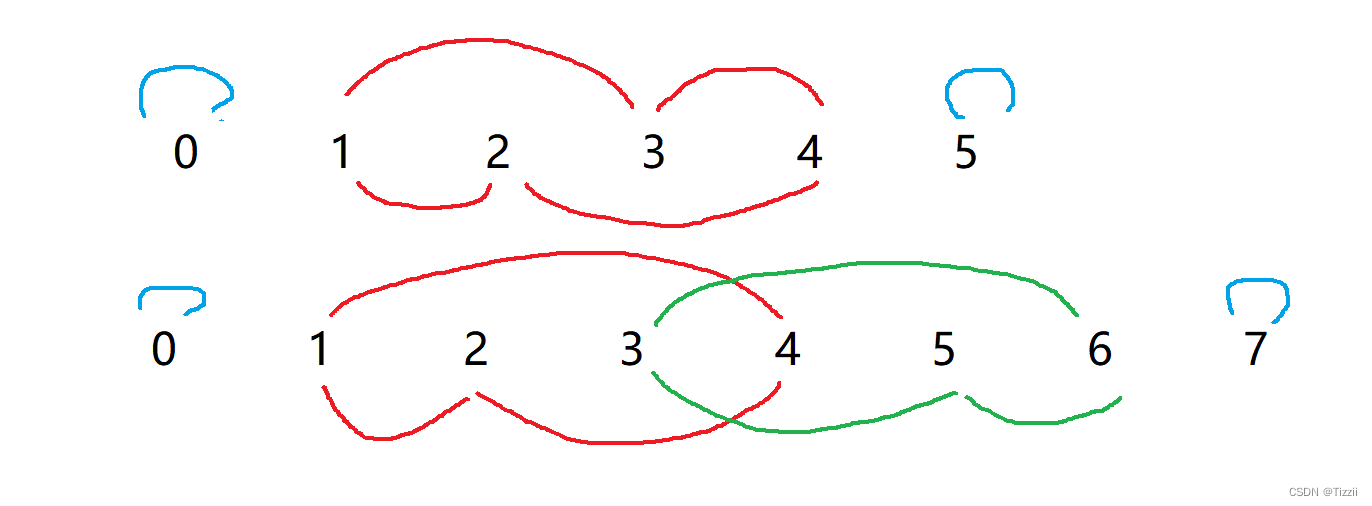
从观察可以发现，1或者n-2必然在最长的环中，因此我们模拟1或者n-2进行交换的次数就是最终的答案。

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

class Solution {
    public int reinitializePermutation(int n) { 
        int i = 1, step = 1;
        while (true) {
            i = i % 2 == 0 ? i / 2 : (n - 1 + i) / 2;
            if (i == 1) return step;
            step++;
        } 
    }
}

class Solution {
public:
    int reinitializePermutation(int n) { 
        int i = 1, step = 1;
        while (true) {
            i = i % 2 ? (n - 1 + i) / 2 : i / 2;
            if (i == 1) return step;
            step++;
        } 
    }
};