2D 小波分解是图像处理中的一种流行技术,使用不同的滤波器将图像分解为不同的频率分量(“近似”和“细节”系数)。该技术对于各种图像处理任务特别有用,例如压缩、去噪、特征提取和边缘检测。
在本文中,我们将演示如何在 Google Colab 中使用 Python 下载高分辨率样本卫星图像,执行 2D 小波分解,可视化高频和低频分量,并使用逆小波方法重建图像,机器学习(ML)算法和耦合线性回归优化模型。为了提高 ML 模型的复杂性,我们将从输入中消除主要组件,并仅使用细节组件重新训练 ML 模型。在整个过程中,我们将评估每种方法在重建阶段的性能,并将 ML 模型的输出可视化。
目录
- 🌟简介
- 🌐 在 Google Colab 中下载卫星图像
- ⚙️ 应用小波分解
- 🔄 使用小波逆变换重建图像
- 🔄 使用 ML 算法重建图像
- 🔄 使用线性回归模型重建图像
- 🔄 使用耦合线性回归模型和优化算法重建图像
- 📈 评估不同的重建方法
- 🔃 使用没有近似系数的 ML 重建图像
- 📄 结论
🌟简介
小波分解的过程包括对图像应用一系列高通和低通滤波器,将图像分离成不同的频率分量。通常,分解分多个阶段完成,在每个级别生成一组近似系数和细节系数。近似系数代表图像的低频分量,而细节系数则捕获高频分量。
小波分解通常与其他技术(例如机器学习)结合使用,以增强图像的分析和处理。通过利用小波的多分辨率功能,研究人员和从业人员可以为各种图像相关任务开发更有效和高效的算法。
总体而言,小波分解已成为图像处理领域的重要工具,并在卫星图像分析、医学成像、信号处理等各个领域都有应用。如果您有兴趣探索 2D 小波分解和 ML 算法在无人机图像中缩小地表温度的主要应用之一
🌐 在 Google Colab 中下载卫星图像
第一步涉及找到下载高分辨率图像的方法。为此,强烈推荐使用 Google 地图的高分辨率航空和卫星图像,尤其是在城市地区。使用 Qiusheng Wu 创建的库可以简化此步骤。确保您已安装必要的组件,包括“segment-geospatial”、“leafmap”和“localtileserver”。接下来,定义所需感兴趣区域 (AOI) 的纬度和经度并继续绘制多边形:
%pip install segment-geospatial leafmap localtileserver
import os
import leafmap
from samgeo import SamGeo, tms_to_geotiff
m = leafmap.Map(center=[37.716956, -120.951107], zoom=20, height="800px")
m.add_basemap("SATELLITE")
m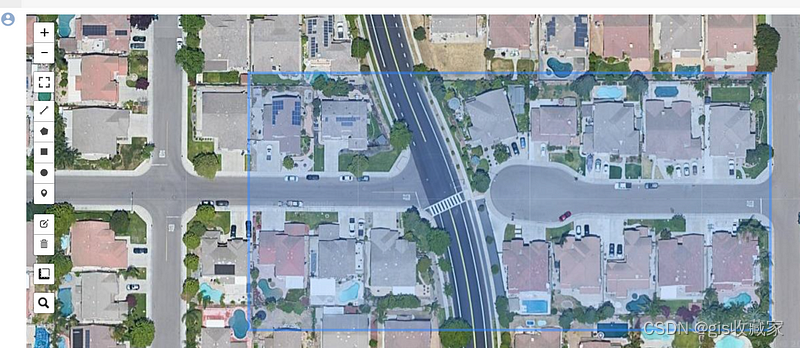
bbox = m.user_roi_bounds()
image = "satellite.tif"
tms_to_geotiff(output=image, bbox=bbox, zoom=20, source="Satellite", overwrite=True)在最后三行中,将感兴趣区域 (AOI) 的边界分配给“bbox”变量,设置输出名称,然后执行“tms_to_geotiff”以指定名称保存卫星图像,在本例中为“satellite” .tif”。
⚙️ 应用小波分解
为了对 2D 图像执行小波分解,我们将使用 Rasterio 库读取下载的图像,并使用 Daubechies 小波家族的一个成员(例如 db1)和“对称”模式实现 2D 分解。
Daubechies 小波是正交小波族,广泛应用于信号处理和图像压缩。“DB”后面的数字表示小波函数中消失矩的数量。小波的消失矩越多,它就越平滑。
另一方面,模式是指执行小波分解的具体方式。该模式可以确定如何计算小波系数以及分解过程如何处理图像的边缘和边界。不同的模式可能导致小波分解输出的变化,特别是在图像的边缘。
小波分解后,原始图像将被划分为不同的频率分量。近似系数表示为cA,而cH、cV和cD分别称为水平、垂直和对角线细节系数。这些系数中的每一个都捕获有关水平、垂直和对角边缘的信息。图像分解后,将绘制每个子带:
import pywt
import rasterio
import numpy as np
import matplotlib.pyplot as plt
# Load GeoTIFF image
with rasterio.open('satellite.tif') as src:
img = src.read(1)
# Perform 2D wavelet decomposition
coeffs = pywt.dwt2(img, 'db1', mode='symmetric')
# Extract detail and approximation coefficients
cA, (cH, cV, cD) = coeffs
# Plot the decomposed coefficients
fig, ax = plt.subplots(2, 2, figsize=(10, 10))
ax[0, 0].imshow(cA, cmap='seismic')
ax[0, 0].set_title('Approximation Coefficient')
ax[0, 1].imshow(cH, cmap='seismic')
ax[0, 1].set_title('Horizontal Detail Coefficient')
ax[1, 0].imshow(cV, cmap='seismic')
ax[1, 0].set_title('Vertical Detail Coefficient')
ax[1, 1].imshow(cD, cmap='seismic')
ax[1, 1].set_title('Diagonal Detail Coefficient')
plt.show()
在上图中,图像的主要部分已保持在近似系数内,而其余元素代表各种方向边缘特征。