给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
创建一个根节点,其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示例 1:
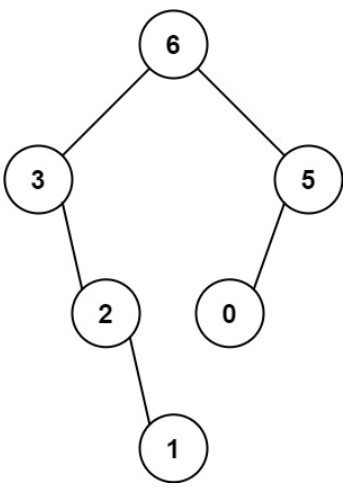
输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。
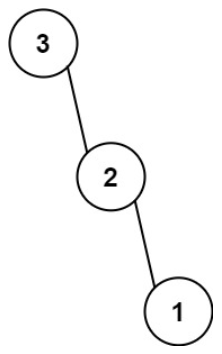
示例 2:
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
输入:nums = [3,2,1]
输出:[3,null,2,null,1]
提示:
1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同
法一:递归构建:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
return build(nums, 0, nums.size() - 1);
}
private:
TreeNode *build(vector<int> &nums, int begin, int end)
{
if (begin > end)
{
return nullptr;
}
int max = -1;
int maxIndex = -1;
for (int i = begin; i <= end; ++i)
{
if (nums[i] > max)
{
max = nums[i];
maxIndex = i;
}
}
TreeNode *node = new TreeNode(max);
node->left = build(nums, begin, maxIndex - 1);
node->right = build(nums, maxIndex + 1, end);
return node;
}
};
如果nums的长度为n,此算法时间复杂度为O(n 2 ^2 2),空间复杂度为O(1)。
法二:单调栈,单调栈用于在线性时间内寻找数组中每个元素左边第一个大(小)于该值的值,或右边第一个大(小)于该值的值。简单介绍一下单调栈,我们遍历nums中的每个元素,每遍历到一个元素,如果栈顶的元素小于当前遍历到的元素,就做出栈操作,直到栈顶元素值大于当前遍历到的元素,或栈为空,这些出栈元素右边第一个大于它们的值就是当前遍历到的元素,做完出栈操作后,栈顶元素就是当前元素的左边第一个大于当前元素的值,然后再把当前遍历到的元素入栈:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
stack<int> s;
vector<TreeNode *> nodeArr(nums.size(), nullptr);
TreeNode *root = nullptr;
for (int i = 0; i < nums.size(); ++i)
{
nodeArr[i] = new TreeNode(nums[i]);
while (!s.empty() && nums[s.top()] < nums[i])
{
nodeArr[i]->left = nodeArr[s.top()];
s.pop();
}
if (!s.empty())
{
nodeArr[s.top()]->right = nodeArr[i];
}
s.push(i);
if (s.size() == 1)
{
root = nodeArr[i];
}
}
return root;
}
};
如果nums的长度为n,此算法时间复杂度为O(n),空间复杂度为O(n)。
法三:线段树,线段树可以logn的效率查找某区间内的最大值,将其与法一中找区间最大值的部分替换,可将找极值的时间复杂度降为logn。线段树的核心在于把数组的每一段的最大值以树来存储,如找数组3、2、1、6、0、5的极值,我们递归地处理它,第一步将其分为两部分,分别为3、2、1和6、0、5,然后极值为这两部分极值中较大的那个,继续递归处理,直到只有单个元素,此时我们就可以知道当前区间的极值了,因为只有一个元素,极值就是它本身,然后递归向上返回,即可求得每一段的极值:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
// 线段树需要开4倍内存
nodeArr.resize(nums.size() * 4 , nullptr);
buildSegmentTree(1, nums.size(), 1, nums);
return buildAns(1, nums.size());
}
private:
TreeNode *buildAns(int left, int right)
{
if (left > right)
{
return nullptr;
}
pair<int, int> max = search(left, right, 1);
int maxIndex = max.first;
int maxValue = max.second;
TreeNode *node = new TreeNode(maxValue);
node->left = buildAns(left, maxIndex - 1);
node->right = buildAns(maxIndex + 1, right);
return node;
}
class Node
{
public:
Node(int left, int right, int maxValue, int maxIndex)
: left(left),
right(right),
maxValue(maxValue),
maxIndex(maxIndex)
{
}
int left;
int right;
int maxValue;
int maxIndex;
};
vector<Node *> nodeArr;
void buildSegmentTree(int left, int right, int x, vector<int> &nums)
{
if (left > right)
{
return;
}
// 如果是叶子结点
if (left == right)
{
nodeArr[x] = new Node(left, right, nums[left - 1], left);
return;
}
int mid = left + (right - left) / 2;
buildSegmentTree(left, mid, 2 * x, nums);
buildSegmentTree(mid + 1, right, 2 * x + 1, nums);
if (nodeArr[2 * x]->maxValue > nodeArr[2 * x + 1]->maxValue)
{
nodeArr[x] = new Node(left, right, nodeArr[2 * x]->maxValue, nodeArr[2 * x]->maxIndex);
}
else
{
nodeArr[x] = new Node(left, right, nodeArr[2 * x + 1]->maxValue, nodeArr[2 * x + 1]->maxIndex);
}
}
pair<int, int> search(int left, int right, int x)
{
if (left == nodeArr[x]->left && right == nodeArr[x]->right)
{
return {nodeArr[x]->maxIndex, nodeArr[x]->maxValue};
}
int mid = (nodeArr[x]->left + nodeArr[x]->right) / 2;
// 如果要查找的范围在当前节点表示范围中点的左边(包括mid,因为建线段树时mid属于左边子树)
// 说明要查找的范围在左子树上
// 之所以与mid做对比,是因为子树的每个节点的范围就是按mid分的
if (right <= mid)
{
return search(left, right, 2 * x);
}
// 如果要查找的范围在当前节点表示范围中点的右边,说明要查找的范围在右子树上
// 此处要用>而非>=,因为mid属于右子树,left只有完全属于右子树时,才只在右子树上查
if (left > mid)
{
return search(left, right, 2 * x + 1);
}
// 如果跨mid,就从两个子树中找
pair<int, int> leftMax = search(left, mid, 2 * x);
pair<int, int> rightMax = search(mid + 1, right, 2 * x + 1);
if (leftMax.second > rightMax.second)
{
return leftMax;
}
else
{
return rightMax;
}
}
};
如果nums的长度为n,此算法时间复杂度为O(nlogn),空间复杂度为O(n)。
法四:ST表,类似法三,ST表能以O(1)的时间查找某一段的极值。ST表的建表用时为O(nlogn),而线段树的建树用时为O(n),但查询时,ST表比线段树快得多。线段树可以动态更改节点值,而ST表不支持,因此ST表更适用于值不会被修改的情况。简单介绍一下ST表,它是一个二维数组,a[i][j]表示从i开始的2的j次方个元素的极值是多少,在查询时,我们把查询区间分为有重叠部分的两段,然后取两段的极值做对比。为什么要取两段?因为二维数组里存的是从要查询的区间开始的、长为2的幂的区间的极值,我们查询的区间长度很有可能不是2的幂,因此需要分为两部分,这两部分一定会有重叠,这也隐含着ST表适用于那种有重叠部分也不影响结果的问题,如极值、求最大公约数等:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
// 由于nums中元素个数最大为1000,因此2的10次方即可完全覆盖
int exp = log(nums.size()) / log(2);
vector<vector<pair<int, int>>> st(nums.size(), vector<pair<int, int>>(exp + 1, {-1, -1}));
for (int i = 0; i < st.size(); ++i)
{
// 初始化,从i开始,长为2的0次方(即1)的极值为它自己
st[i][0] = {nums[i], i};
}
// j最大为9,我们只会用到2的9次方的值,因为查找时我们会把区间分为两段
for (int j = 1; j < st[0].size(); ++j)
{
// 循环条件部分保证了不会索引超出
for (int i = 0; i + (1 << (j - 1)) < nums.size(); ++i)
{
// st[i][j - 1]是2的j-1次方个数字,为第一段
// st[i + (1 << (j - 1))][j - 1]也是2的j-1次方个数字,从第一段的后面一个位置开始
// 注意st[i + (1 << (j - 1))][j - 1]中的i + (1 << (j - 1))部分是循环条件
st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}
}
return build(0, nums.size() - 1, nums, st);
}
private:
TreeNode *build(int left, int right, vector<int> &nums, vector<vector<pair<int, int>>> &st)
{
if (left > right)
{
return nullptr;
}
// 以2为底,范围内数字个数的对数,将结果再去掉小数,这是最大的两段长度
int num = log(right - left + 1) / log(2);
// 两段会有交叉,如果left为0,right为5,则num为2
// 此时会取从0开始的4个数字的极值和从1开始的4个数字的极值两者更大值
const pair<int, int> &target = max(st[left][num], st[right - (1 << num) + 1][num]);
int maxValue = target.first;
int maxIndex = target.second;
TreeNode *node = new TreeNode(maxValue);
node->left = build(left, maxIndex - 1, nums, st);
node->right = build(maxIndex + 1, right, nums, st);
return node;
}
};
此算法时间复杂度为O(nlogn),用于建表;空间复杂度为O(nlogn)。