一、样本数据描述
城镇居民人均消费支出水平包括食品、衣着、居住、生活用品及服务、通信、文教娱乐、医疗保健和其他用品及服务支出这八项指标来描述。表中列出了2016年我国分地区的城镇居民的人均消费支出的原始数据,数据来源于2017年的《中国统计年鉴》,现要求对下面的数据进行聚类分析。
x1:食品烟酒支出,x2:衣着支出,x3:居住支出,x4:生活用品和服务支出,
x5:交通通信支出,x6:教育文化娱乐支出,x7:医疗保健支出,x8:其他用品和服务支出
City,X1,X2,X3,X4,X5,X6,X7,X8
北京,8070.4,2643,12128,2511,5077.9,4054.7,2629.8,1140.6
天津,8679.6,2114,6187.3,1663.8,3991.9,2643.6,2172.2,892.2
河北,4991.6,1614.4,4483.2,1351.1,2664.1,1991.3,1549.9,460.4
山西,3862.8,1603,3633.8,951.6,2401,2439,1651.6,450.1
内蒙古,6445.8,2543.3,4006.1,1565.1,3045.2,2598.9,1840.2,699.9
辽宁,6901.6,2321.3,4632.8,1558.2,3447,3018.5,2313.6,802.8
吉林,4975.7,1819,3612,1107.1,2691,2367.5,2059.2,534.9
黑龙江,5019.3,1804.4,3352.4,1018.9,2462.9,2011.5,2007.5,468.3
上海,10014.8,1834.8,13216,1868.2,4447.5,4533.5,2839.9,1102.1
江苏,7389.2,1809.5,6140.6,1616.2,3952.4,3163.9,1624.5,736.6
浙江,8467.3,1903.9,7385.4,1420.7,5100.9,3452.3,1691.9,645.3
安徽,6381.7,1491,3931.2,1118.4,2748.4,2233.3,1269.3,432.9
福建,8299.6,1443.5,6530.5,1393.4,3205.7,2461.5,1178.5,492.8
江西,5667.5,1472.2,3915.9,1028.6,2310.6,1963.9,887.4,449.6
山东,5929.4,1977.7,4473.1,1576.5,3002.5,2399.3,1610,526.9
河南,5067.7,1746.6,3753.4,1430.2,1993.8,2078.8,1524.5,492.8
湖北,6294.3,1557.4,4176.7,1163.8,2391.9,2228.4,1792,435.6
湖南,6407.7,1666.4,3918.7,1384.1,2837.1,3406.1,1362.6,437.4
广西,5937.2,886.3,3784.3,1032.8,2259.8,2003,1065.9,299.3
海南,7419.7,859.6,3527.7,954,2582.3,1931.3,1399.8,341
重庆,6883.9,1939.2,3801.1,1466,2573.9,2232.4,1700,434.4
四川,7118.4,1767.5,3756.5,1311.1,2697.6,2008.4,1423.4,577.1
贵州,6010.3,1525.4,3793.1,1270.2,2684.4,2493.5,1050.1,374.6
云南,5528.2,1195.5,3814.4,1135.1,2791.2,2217,1526.7,414.3
陕西,5422,1542.2,3681.5,1367.7,2455.7,2474,2016.7,409
甘肃,5777.3,1776.9,3752.6,1329.1,2517.9,2322.1,1583.4,479.9
青海,5975.7,1963.5,3809.4,1322.1,3064.3,2352.9,1750.4,614.9
宁夏,4889.2,1726.7,3770.5,1245.1,3896.5,2415.7,1874,546.6
新疆,6179.4,1966.1,3543.9,1543.8,3074.1,2404.9,1934.8,581.5
广东,9421.6,1583.4,6410.4,1721.9,4198.1,3103.4,1304.5,870.1
西藏,8727.8,1812.5,3614.5,983.0,2198.4,922.5,585.3,596.5
二、读入数据
df<-read.csv('f:/桌面/人均消费支出.csv')
head(df)
head(df)
city x1 x2 x3 x4 x5 x6 x7 x8
1 北京 8070.4 2643.0 12128.0 2511.0 5077.9 4054.7 2629.8 1140.6
2 天津 8679.6 2114.0 6187.3 1663.8 3991.9 2643.6 2172.2 892.2
3 河北 4991.6 1614.4 4483.2 1351.1 2664.1 1991.3 1549.9 460.4
4 山西 3862.8 1603.0 3633.8 951.6 2401.0 2439.0 1651.6 450.1
5 内蒙古 6445.8 2543.3 4006.1 1565.1 3045.2 2598.9 1840.2 699.9
6 辽宁 6901.6 2321.3 4632.8 1558.2 3447.0 3018.5 2313.6 802.8
三、使用系统聚类法进行聚类分析
使用R语言中的hclust()进行聚类分析,调用格式为
hclust(d,method='comlete',member=NULL)
默认使用最长距离法,还可以使用下面几种方法:
1、类平均法(average linkage)2、重心法(centroid method)3、中间距离法(median method)4、最长距离法(complete method)5、最短距离法(single method)6、离差平方和法(ward method)7、密度估计法(density method)
attach(df)
df.hc<-hclust(dist(df[,2:9])) #将聚类结果保存在变量df.hc中
plot(df.hc,hang=-1) #绘制树状聚类图,使用默认的最长距离法进行聚类分析。
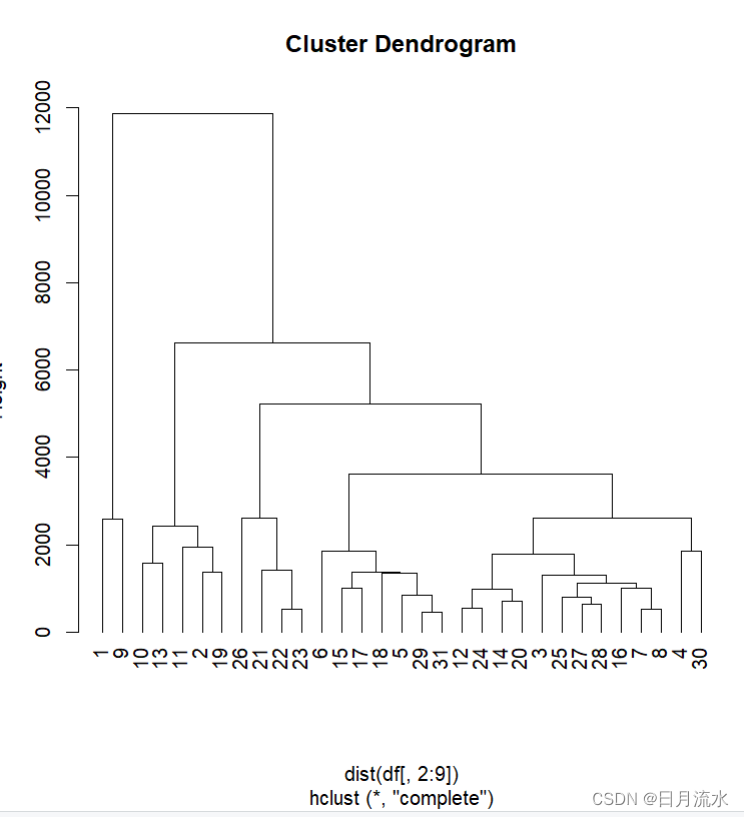
将样本数据分为3类
re<-rect.hclust(df.hc,k=3)
得到把分类框起来的聚类图:
 从聚类图中可以看到:北京上海为第一类,江苏福建浙江天津广东为第二类,其余为第三类。
从聚类图中可以看到:北京上海为第一类,江苏福建浙江天津广东为第二类,其余为第三类。
df.id<-cutree(df.hc,k=3)
df.id
df.id [1] 1 2 3 3 3 3 3 3 1 2 2 3 2 3 3 3 3 3 2 3 3 3 3 3 3 3 3 3 3 3 3
得到了31个样本具体的分类数据。
四、使用模糊聚类的方法进行聚类分析
row.names(df)<-df[,1]
df<-df[,-1]
library(cluster)
fy<-fanny(df,3)
运行得到:
summary(fy)
Fuzzy Clustering object of class 'fanny' :
m.ship.expon. 2
objective 15896.27
tolerance 1e-15
iterations 49
converged 1
maxit 500
n 31
Membership coefficients (in %, rounded):
[,1] [,2] [,3]
北京 51 25 25
天津 65 17 17
河北 10 45 45
山西 14 43 43
内蒙古 13 44 44
辽宁 24 38 38
吉林 9 46 46
黑龙江 9 45 45
上海 49 25 25
江苏 54 23 23
浙江 69 16 16
安徽 8 46 46
福建 58 21 21
江西 9 46 46
山东 10 45 45
河南 9 45 45
湖北 8 46 46
湖南 13 43 43
广东 67 16 16
广西 10 45 45
海南 17 41 41
重庆 11 45 45
四川 13 44 44
贵州 7 46 46
云南 7 46 46
西藏 27 36 36
陕西 7 46 46
甘肃 5 47 47
青海 7 47 47
宁夏 14 43 43
新疆 8 46 46
Fuzzyness coefficients:
dunn_coeff normalized
0.4172668 0.1259002
Membership coefficients (in %, rounded):运行得到了模糊矩阵的系数,也就是各样品的分类系数,那么如果该样本在这三个类中的某类系数最大,该样本就属于该类。
Closest hard clustering:为按照分类系数在各类取值的大小得到的聚类结果。很明显该聚类结果和系统聚类法得到的结果存在显著差异。
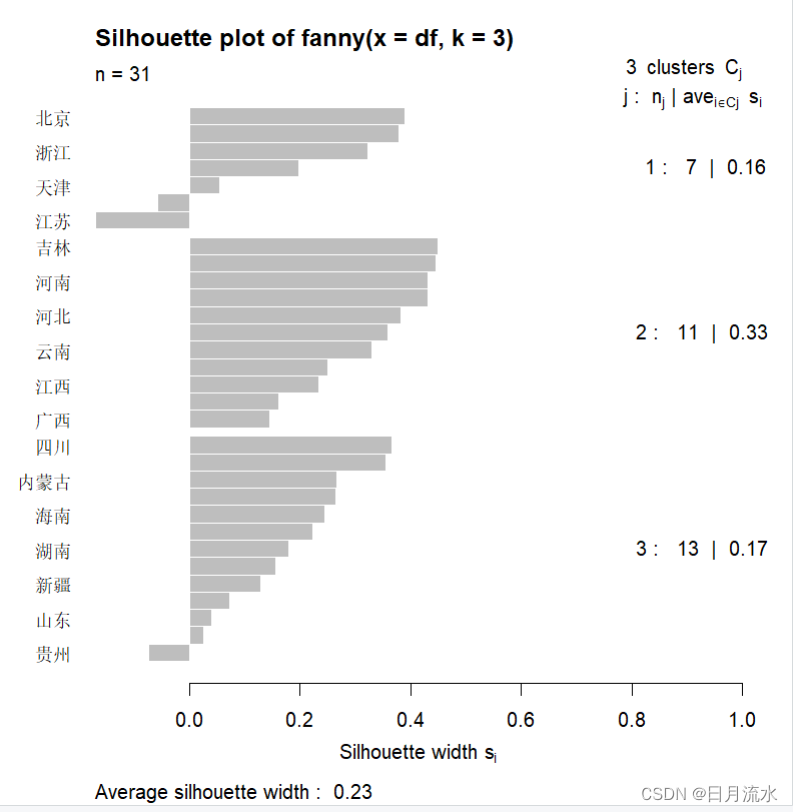
plot(fy)
运行得到:
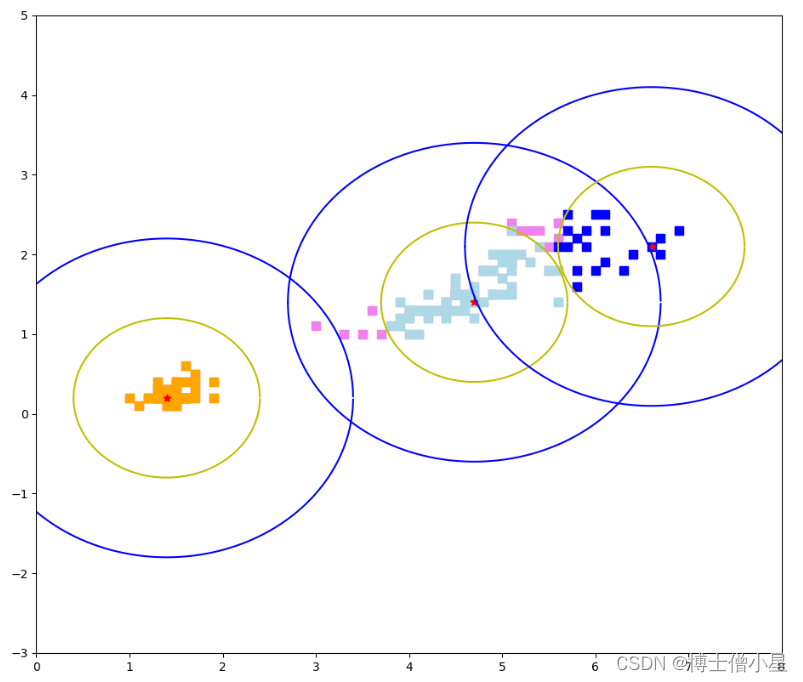
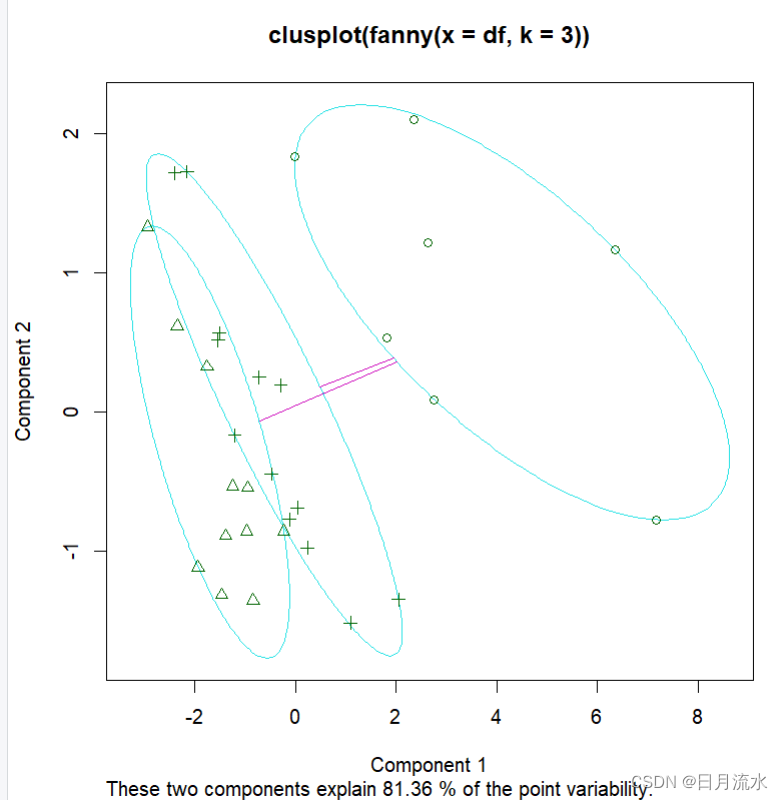
1、样本的主成分分类图
31个样本在两个主成分得分绘制在直角坐标系中所描述的点,每个样本在图中用不同的标记标出,每一类都被框起来。从图中可以看到第一类7个样本为最右上角的图形和第二类三类可以明显区分,第二类和第三类不能明显区分。
2、样本的侧影图,从下图侧影图中可以直观的看出各类包含哪些样本。