算法学习06：数组模拟：单/双链表，栈和队列，单调栈/队列

---

---

前言

---

提示：以下是本篇文章正文内容：

一、链表

---

---

---

---

1.单链表

---

---

---

---

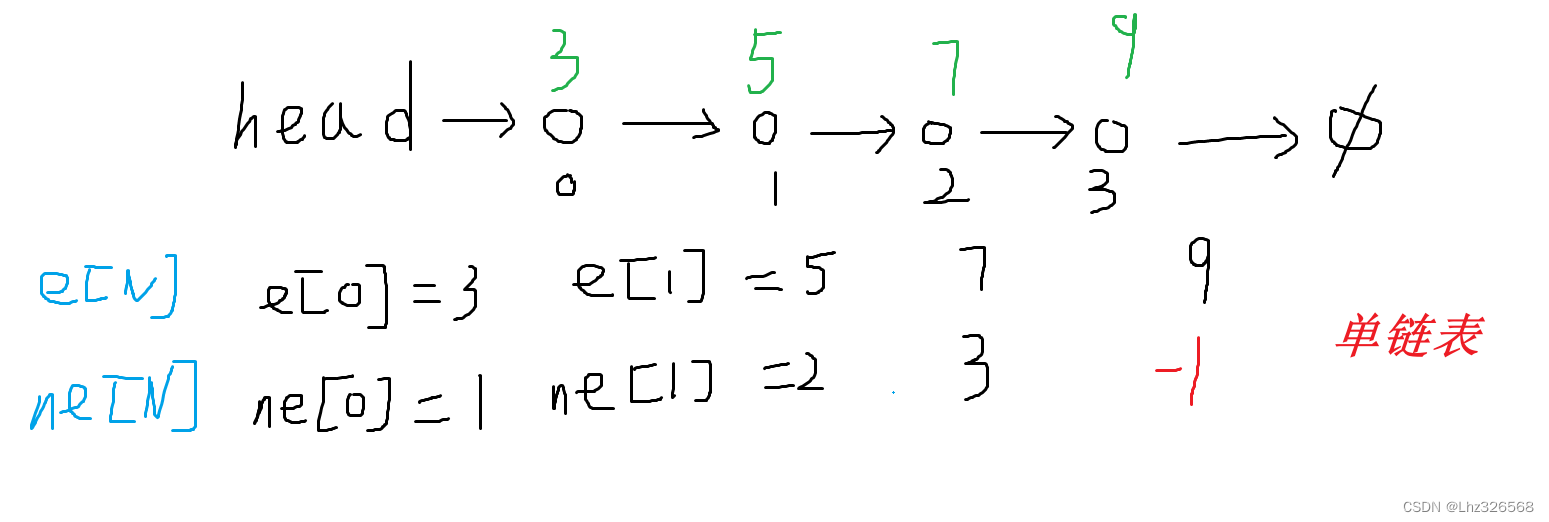
#include <iostream>

using namespace std;

const int N = 100000 + 10;

//head：表示头结点的下标
//e[i]：表示结点i的值
//ne[i]：表示结点i的next指针是多少
//idx：存储当前已经用到了那个点（从0开始）
int head, e[N], ne[N], idx;

//初始化：
void init()
{
	head = -1;
	idx = 0;
 } 

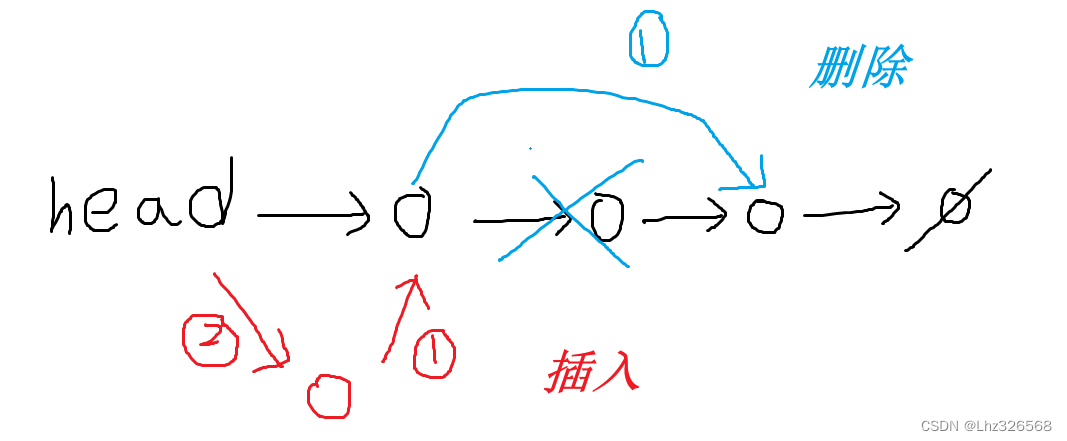
//将x插入到头结点：
void add_to_head(int x)
{
	e[idx] = x;
	ne[idx] = head;
	head = idx;
	idx ++;
 } 
 
 // 将x插入到下标是k的点后面：
 void add(int k, int x)
 {
 	e[idx] = x;
 	ne[idx] = ne[k];
 	ne[k] = idx;
 	idx ++;
  } 
  
// 将下标是k的点后面的点删除
void remove(int k)
{
	ne[k] = ne[ne[k]];
 } 


int main()
{
	int m;
	cin >> m;
	
	init();
	
	while(m --)
	{
		char op;
		int x, k;
		cin >> op;
		if(ip == 'H')
		{
			cin >> x;
			add_to_head(x);
		}
		else if(ip == 'D')
		{
			cin >> k;
			if(!k) head = ne[head];//注意1：删除头结点 
			remove(k - 1);
		}
		else
		{
			cin >> k >> x;
			add(k - 1, x);
		}
	}
	
	for(int i - head; i != -1; i = ne[i]) cout << e[i] << ' ';
	cout << endl;
	return 0;
}

---

---

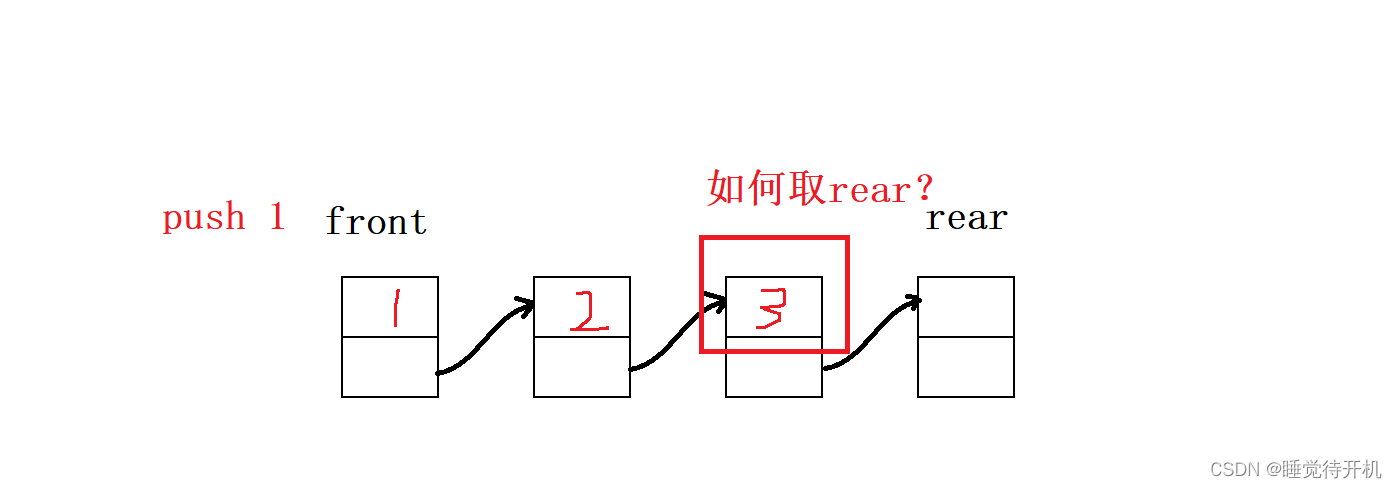
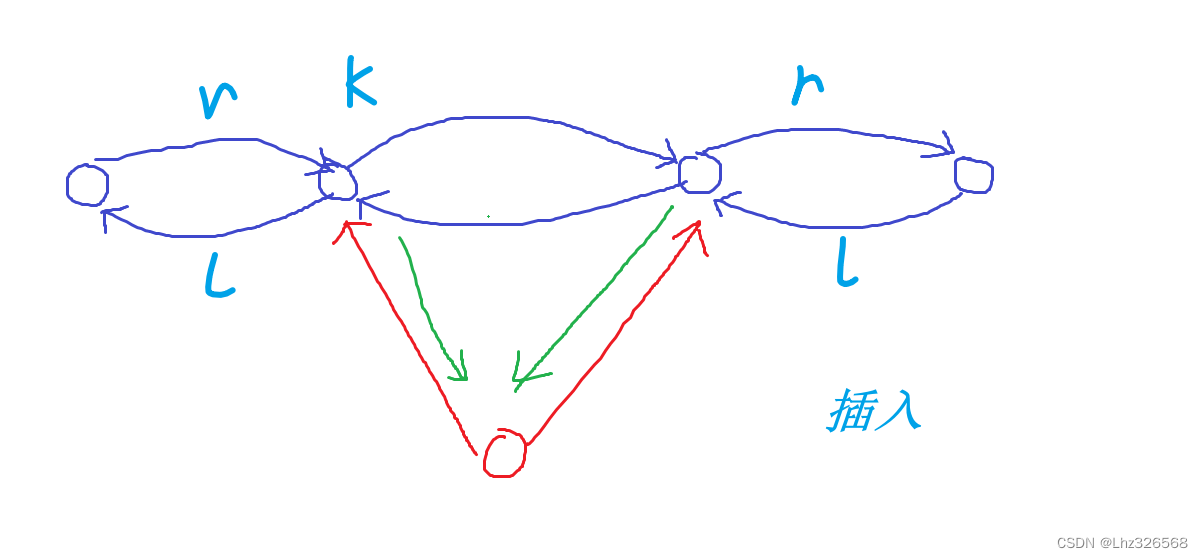
2.双链表

---

---

---

---

---

---

---

---

#include <iostream>

using namespace std;

const int N = 100000 + 10;

int m;
int e[N], l[N], r[N], idx;

//初始化：
void init()
{
	//0表示左端点，1表示右端点
	r[0] = 1, l[1] = 0;
	idx = 2; 
 } 
 
 //在下标是k的结点后，插入x ： 
void add(int k, int x)
{
	e[idx] = x;
	r[idx] = r[k];//idx的右边 
	l[idx] = k;//idx的左边 
	l[r[k]] = idx;//k右边结点的左边 
	r[k] = idx;//k的右边 
}

//删除第k个点：
void remove(int k)
{
	r[l[k]] = r[k];//k左边节点的右边，连接k的右边的结点 
	l[r[k]] = l[k];//k右边结点的左边，连接k的左边的结点 
 } 

---

---

二、栈和队列

1.普通栈、队列

---

---

---

---

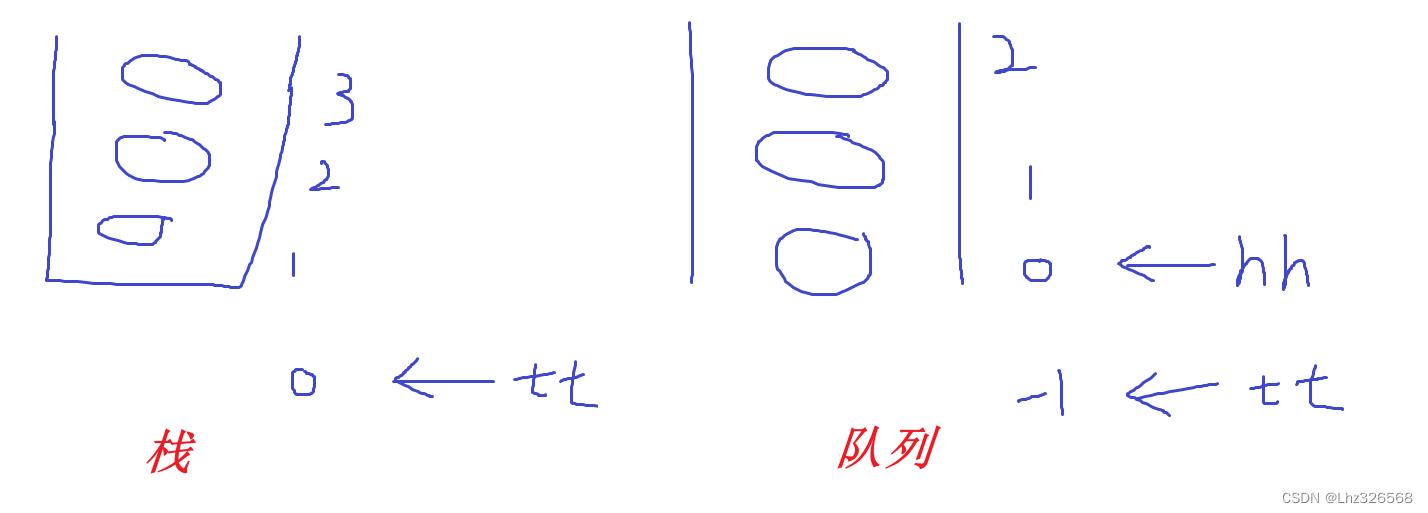
#include <iostream>

using namespace std;

const int N = 100000 + 10;

// ***************************栈：

int stk[N], tt;//stk：栈， tt：栈顶

//插入：
stk[++ tt] = x;//从 1 开始

//弹出：
tt --;

// 判断栈是否为空：(伪代码)
if(tt > 0) not empty;
else empty;

// 栈顶 ：
stk[tt];

// ***************************队列：
int q[N], hh, tt = -1;//hh：对头， tt：对尾

// 插入：
q[++ tt] = x; 

// 弹出：
hh ++;

// 判断队列是否为空：
if(hh <= tt) not empty;
else empty;

// 取出对头元素： 
q[hh];
 

---

---

2.单调栈

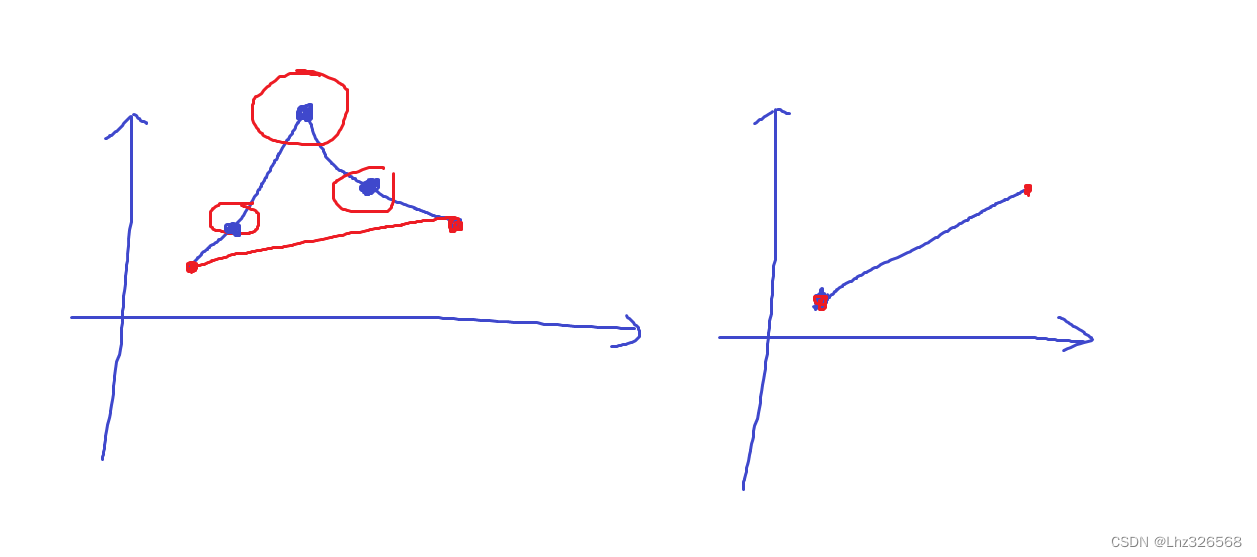
例题：给一个长度为N的整数序列，输出每个数昨天第一个比他小的数，如果不存在就输出-1。

---

---

---

---

---

---

//例题：给一个长度为N的整数序列，输出每个数昨天第一个比他小的数，
//如果不存在就输出-1。
#include <iostream>

using namespace std;

const int N = 100000 + 10;

int n;
int stk[N], tt;

int main()
{
	cin >> n;
	
	for(int i = 0; i < n; i ++)
	{
		int x;
		cin >> x;
		//单调栈 
		//在我们维护的栈中，移去比当前数“x”大的数 
		while(tt & stk[tt] >= x) tt--;
		//此时，栈顶元素就是 最近的 小于x的数
		if(tt) cout << stk[tt] << endl;
		else cout << -1 << end;
		
		stk[++ tt] = x;//将x进栈，仍然可以维护 单调栈。 
	}
	
	return 0;
}

3.单调队列

题目：给定一个大小为n<=10^6的数组，有一个大小为k的滑动窗口，它从数组的最左边移动感到最右边，你只能找窗口中看到k个数字。
你的任务是确定滑动窗口位于每个位置是，窗口中的最小值和最大值。

---

---

---

//题目：给定一个大小为n<=10^6的数组，有一个大小为k的滑动窗口，
//它从数组的最左边移动感到最右边，你只能找窗口中看到k个数字。
//你的任务是确定滑动窗口位于每个位置是，窗口中的最大值和最小值。

#include <iostream>

using namespace std;

const int N = 100000 + 10;

int n, k;
int a[N], q[N];//q：队列，队列存储的是 下标 

int main()
{
	scanf("%d%d", &n, &k);
	for(int i = 0; i < n; i ++) scnaf("%d", %a[i]);
	
	//窗口中的最小值
	int hh = 0, tt = -1;
	for(int i = 0; i < n; i ++) 
	{
		//判断对头是否已经 划出窗口：
		//使用if？每次移动一格。 
		if(hh <= tt && i - k + 1 > q[hh]) hh ++; 
		//将窗口内大于的元素 出队列（为什么从后面出队列？分析题目所得。
		while(hh <= tt && a[q[tt] >= a[i]]) tt --;
		q[++ tt] = i;//要先加入，i对应的值可能是最小的 
		if(i >= k - 1) printf("%d", a[q[hh]]);	
	 } 
	 put(" "); 
	//窗口中的最大值
	 int hh = 0, tt = -1;
	for(int i = 0; i < n; i ++) 
	{
		//判断对头是否已经 划出窗口：
		if(hh <= tt && i - k + 1 > q[hh]) hh ++;
		while(hh <= tt && a[q[tt] <= a[i]]) tt --;
		q[++ tt] = i;//i对应的值可能是最大的 
		if(i >= k - 1) printf("%d", a[q[hh]]);	
	 } 
	 put(" "); 
	return 0;
 } 

---

---

三、 拓展：ios::sync_with_stdio(false) 和 cin.tie(0) 对cin，cout速率的影响：

拓展：关于输入的速率问题
（1）cin，cout (1394ms)
（2）scanf，printf (133ms)
（3）ios::sync_with_stdio(false); + cin (1182ms)
（4）cin.tie(0); (141ms)
应用别人的博客来解释cin，cout的速率问题😍

---

总结

提示：这里对文章进行总结：
💕💕💕