题目

102. 二叉树的层序遍历

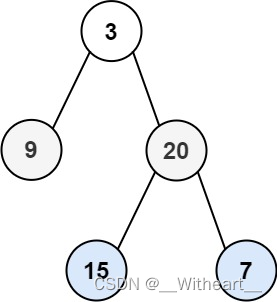
给定二叉树的根节点 root，返回节点值的层序遍历结果。即逐层地，从左到右访问所有节点。

示例 1：

输入：root = [3,9,20,null,null,15,7] 输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1] 输出：[[1]]

示例 3：

输入：root = [] 输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000

思考

• 二叉树的层序遍历是比较常见的题目
• 此题的难点是如何把每层的节点归类为同一行，如果全部节点都放入队列中直接进行遍历，那么访问的节点可能超出一层
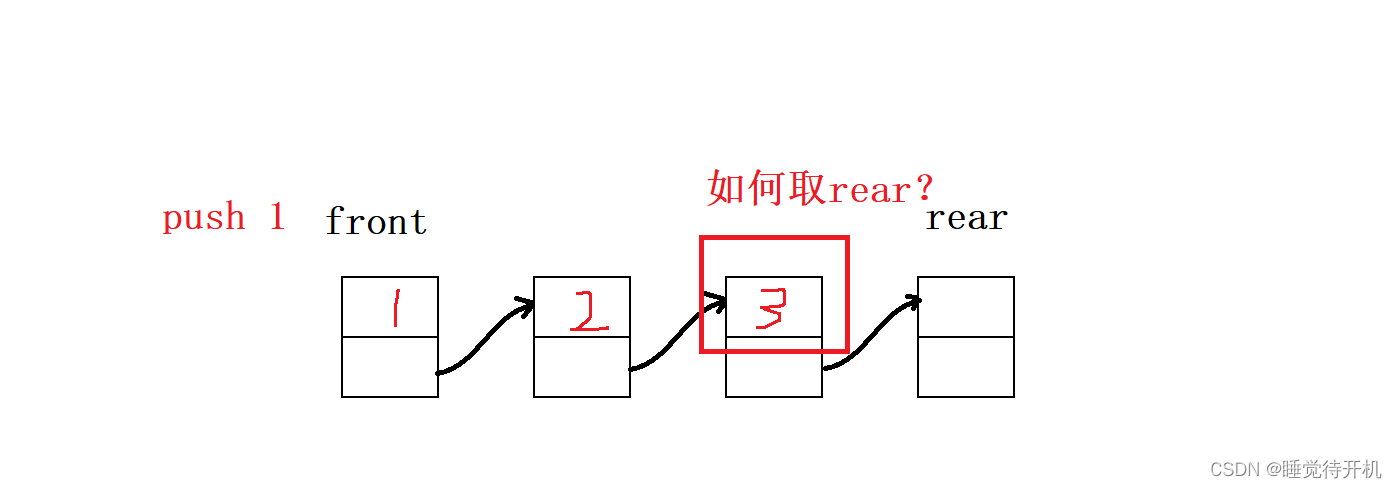
• 是否需要一个变量，记录本层的节点个数。开始循环遍历队列，本次遍历根据本层的节点个数，将本层节点循环遍历记录下来，在这个过程中同时将本层节点可以访问到的下一层节点存入队列，由于先记录了本层的节点个数，所以这个循环不会超出本层
• 在这种情况下，每次循环都将本层的节点全部输出，然后将下一层的节点全部加入，所以在开始输出和加入之前，队列中元素的个数就是本层所有节点的个数，所以可以像这样优雅地记录本层的节点个数

for(int i=q.size(); i>0; --i)

解法1：简洁解法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> ans;
        if(!root) return ans;
        queue<TreeNode*> q;
        q.push(root);
        while(!q.empty()){
            vector<int> v;
            for(int i=q.size(); i>0; --i){
                v.push_back(q.front()->val);
                if(q.front()->left) q.push(q.front()->left);
                if(q.front()->right) q.push(q.front()->right);
                q.pop();
            }
            ans.push_back(v);
        }
        return ans;
    }
};

解法2：由二维数组联想到使用二维队列

• 二维队列中每个小队列包含一层的所有元素

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> ans;
        if(!root) return ans;
        queue<queue<TreeNode*>> layerSeq;
        queue<TreeNode*> q;
        q.push(root);
        layerSeq.push(q);
        while(!layerSeq.empty()){
            vector<int> v;
            queue<TreeNode*> q;
            while(!layerSeq.front().empty()){
                v.push_back(layerSeq.front().front()->val);
                if(layerSeq.front().front()->left) q.push(layerSeq.front().front()->left);
                if(layerSeq.front().front()->right) q.push(layerSeq.front().front()->right);
                layerSeq.front().pop();
            }
            if(!q.empty()) layerSeq.push(q);
            layerSeq.pop();
            ans.push_back(v);
        }
        return ans;
    }
};