C语言数据结构之二叉堆

news2024/10/6 2:24:33

愿你千山暮雪

海棠依旧

不为岁月惊扰平添忧愁

🎥前期回顾-二叉树

🔥数据结构专栏

期待小伙伴们的支持与关注！！！

目录

前期回顾

二叉堆的概念及结构 

 二叉堆的创建

顺序表的结构声明

 顺序表的创建与销毁

二叉堆的插入 

 二叉堆显示堆顶元素

 二叉堆的删除

 二叉堆的判空

整体代码实现

前期回顾

二叉树的顺序结构 

普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。而我们今天学的 堆 总是一棵 完全二叉树

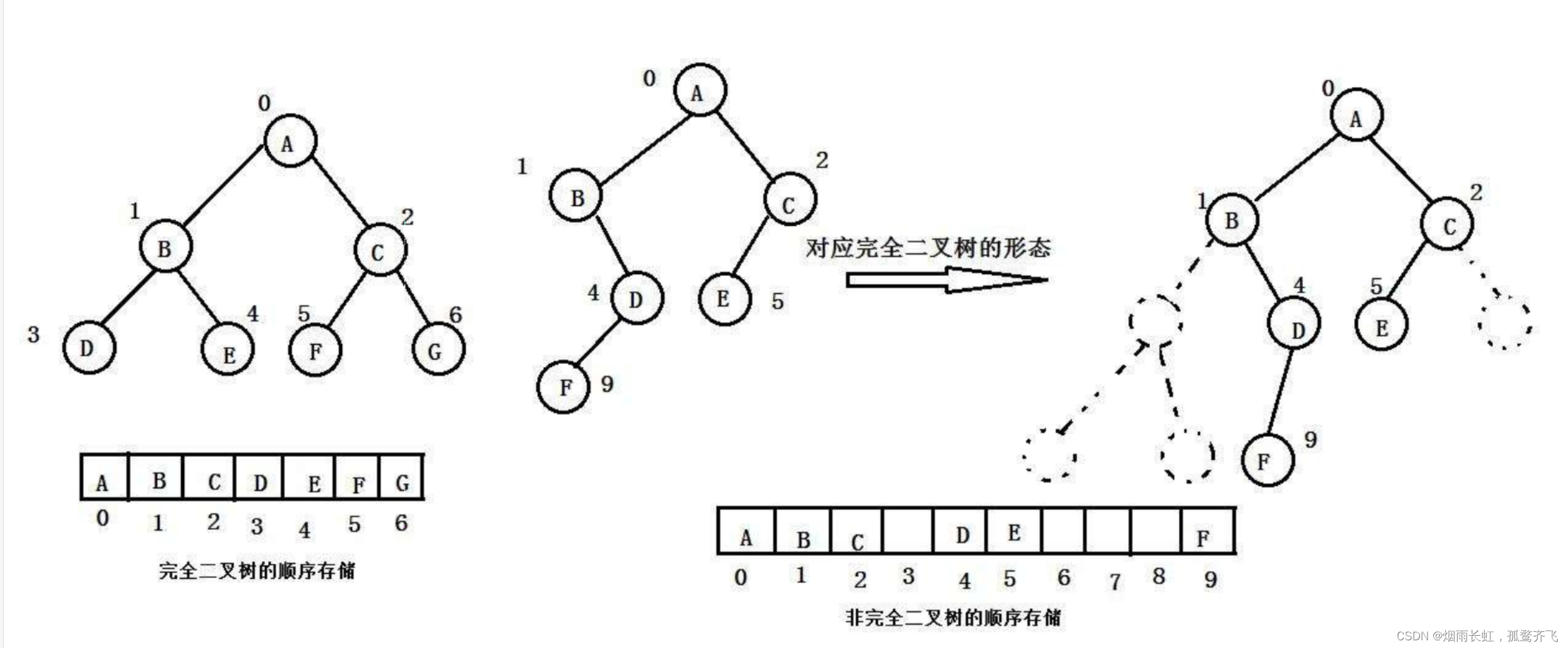
作为一棵完全二叉树，二叉堆可以用一个1-n 的数组来存储

对于双亲节点p，p*2+1即为左孩子，p*2+2即为右孩子

对于孩子节点 child 求双亲结点 parent 即 parent = (child - 1) / 2

同时，用size记录当前二叉堆中节点的个数

顺序存储的结论

如果 i 为0，则 i 表示的节点为根节点，否则 i 节点的双亲节点为 (i - 1)/2
如果 2 * i + 1 小于节点个数，则节点 i 的左孩子下标为 2 * i + 1，否则没有左孩子
如果 2 * i + 2 小于节点个数，则节点 i 的右孩子下标为 2 * i + 2，否则没有右孩子

二叉堆（Binary Heap）是最简单、常用的堆，是一棵符合堆的性质的 完全二叉树

它可以实现 O(log⁡n) 的 插入 或 删除 某个值，并且 O(1) 地查询 最大（或最小）值

二叉堆的概念及结构 

概念#

堆在运用范围上：用来在一组变化频繁（发生增删查改的频率较高）的数据集中查找最值

堆在物理层面上：表现为一组连续的数组区间 long[ ] array 将整个数组看作是堆

堆在逻辑结构上：一般被视为是一颗完全二叉树

结构#

如果有一个关键码的集合K = {K0 ，K1 ，K2 ，…，Kn-1 }，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中并满足：Ki <=K2*i+1 且 Ki<=K2*i+2 ( Ki >=K2*i+1 且Ki>=K2*i+2 ) i = 0，1，2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

堆的性质#

堆中某个节点的值总是不大于或不小于其双亲节点的值
堆总是一棵完全二叉树
小根堆#

<1>双亲节点的值 小于或等于 子节点的值

大根堆#

<2>双亲节点的值 大于或等于 子节点的值

 二叉堆的创建

下面以 小根堆 进行演示

顺序表的结构声明

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int HeapDataType;

typedef struct Heap
{
	int size;
	int capacity;
	HeapDataType* data;
}HP;

 顺序表的创建与销毁

创建

void HPInit(HP* php)
{
	assert(php);
	php->data = NULL;
	php->capacity = php->size = 0;
}

销毁

void HPDestroy(HP* php)
{
	assert(php);
	free(php->data);
	php->data = NULL;
	php->capacity = 0;
	php->size = 0;
}

二叉堆的插入 

 顺序表的基本结构

void HPPush(HP* php, HeapDataType x)
{
	assert(php);
	if (php->capacity == php->size)
	{
		int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;
		HeapDataType* newNode = (HeapDataType*)realloc(php->data, sizeof(HeapDataType) * newcapacity);
		if (newNode == NULL)
		{
			perror("realloc");
			exit(-1);
		}
		php->data = newNode;   
		php->capacity = newcapacity;
	}
	php->data[php->size] = x;
	php->size++;
	AdjustUp(php->data, php->size - 1);
}

交换函数 交换孩子与双亲之间的位置

void Swap(HeapDataType* n, HeapDataType* m)
{
	HeapDataType tmp = *n;
	*n = *m;
	*m = tmp;  
}

我们以下面这两颗树为例

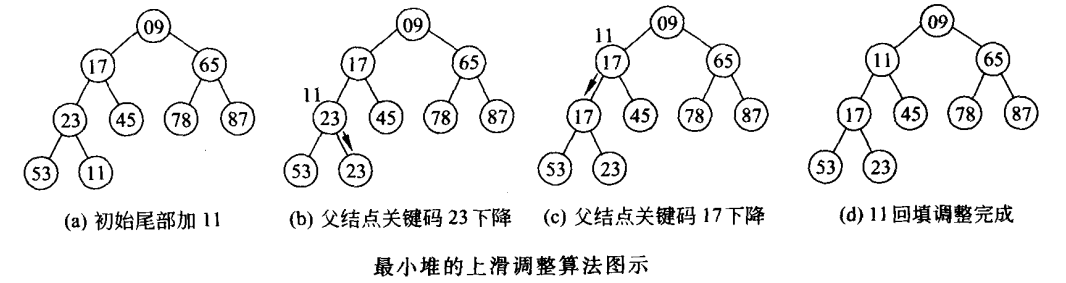
如何 插入 元素，同时维护二叉堆的性质？

如果我们想在二叉堆中插入一个数 11 或者 10

我们可以采用上调算法：该子节点不断与双亲节点比较，如果比双亲节点 小 就与之交换

直到不大于双亲节点或成为根节点为止

上调算法

void AdjustUp(HeapDataType* data, int child)
{
			// 找到child的双亲
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (data[child] < data[parent])
		{
			// 如果孩子小于双亲就进行交换
			Swap(&data[child], &data[parent]);
			// 关系转换
			child = parent;
			// 需要继续向上调整
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

 二叉堆显示堆顶元素

HeapDataType HPTop(HP* php)
{

	assert(php);
	return php->data[0];
}

 二叉堆的删除

 顺序表的基本结构

void HPPop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	// 堆顶元素与末尾元素进行交换，删除最后一个位置
	Swap(&php->data[0], &php->data[php->size-1]);
	php->size--;
	// 针对堆顶位置，做向下调整
	AdjustDown(php->data, php->size, 0);
}

如何 删除 堆顶端的元素，同时维护堆的性质?


实际的操作是将堆顶元素对堆中最后一个元素交换，堆的元素个数-1，然后再从根结点开始进行一次从上向下的调整。调整时先在左右孩子结点中找最小的，如果双亲结点比这个最小的子结点还小说明不需要调整了，反之将双亲结点和它交换后再考虑后面的结点。

下调算法

确定目标子节点： 

parent 从根节点开始，假设目标子节点为左孩子 child = parent*2+1 ，当左孩子在数组范围之内时进入循环

如果 child + 1 (即右孩子)没超过范围 且 data[child+1] < data[child]，则说明右孩子为目标子节点，更新目标子节点 child = child + 1

更新目标亲子关系：

此时 child 为目标子节点，然后再与 parent 双亲结点比较判断是否交换

void AdjustDown(HeapDataType* data, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
			// 兄弟比较，取小为child
		if (child + 1 < n && data[child+1] < data[child])
		{
			child++;
		}
		if (data[child] < data[parent])
		{
			// 父子比较，判断是否交换
			Swap(&data[child], &data[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
<1>将堆顶元素对堆中最后一个元素交换
<2>将堆中有效数据个数减少一个
<3>对堆顶元素进行向下调整

 二叉堆的判空

bool HPEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}

整体代码实现

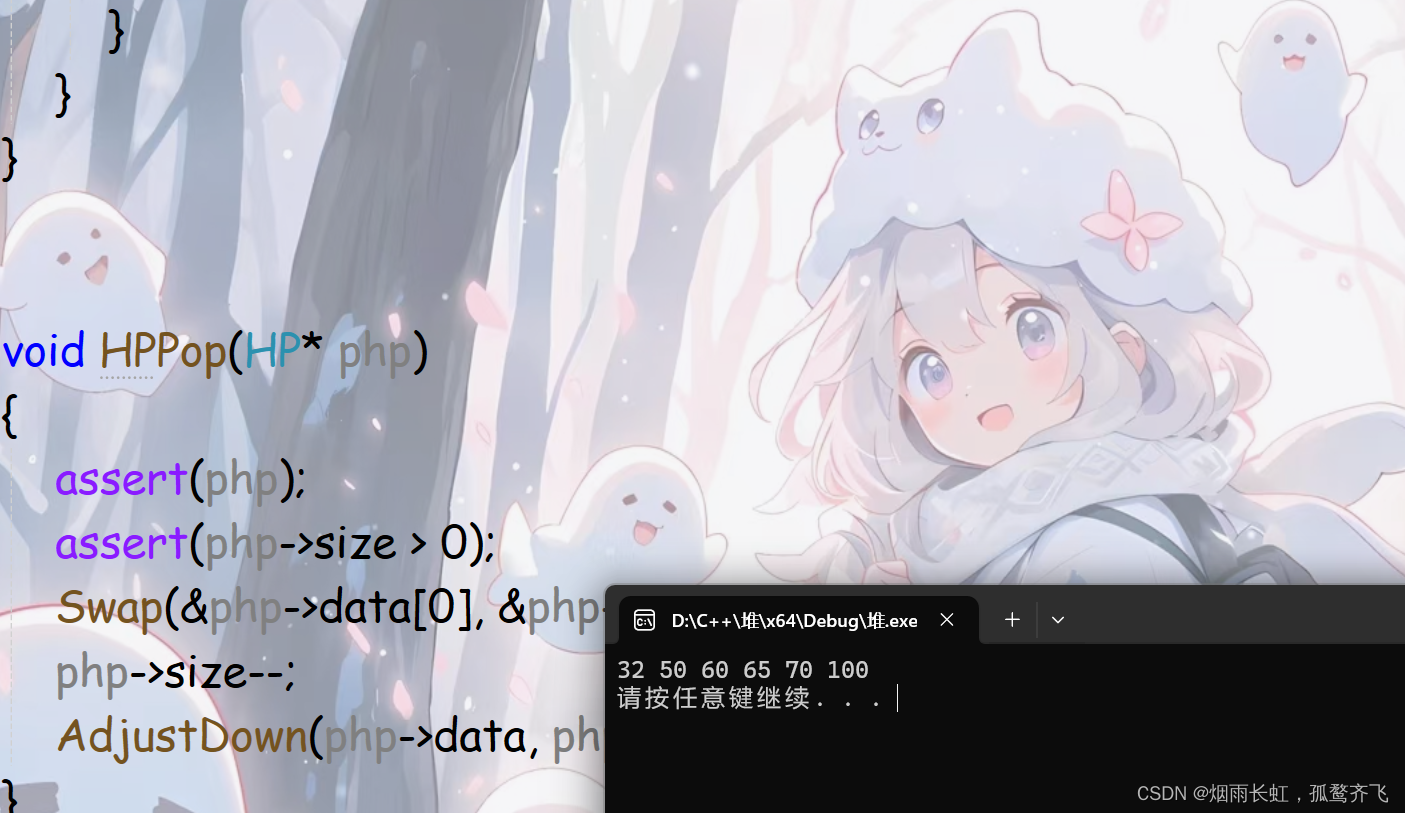
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int HeapDataType;

typedef struct Heap
{
	int size;
	int capacity;
	HeapDataType* data;
}HP;

void HPInit(HP* php)
{
	assert(php);
	php->data = NULL;
	php->capacity = php->size = 0;
}

void HPDestroy(HP* php)
{
	assert(php);
	free(php->data);
	php->data = NULL;
	php->capacity = 0;
	php->size = 0;
}

void Swap(HeapDataType* n, HeapDataType* m)
{
	HeapDataType tmp = *n;
	*n = *m;
	*m = tmp;  
}

void AdjustUp(HeapDataType* data, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (data[child] < data[parent])
		{
			Swap(&data[child], &data[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

void HPPush(HP* php, HeapDataType x)
{
	assert(php);
	if (php->capacity == php->size)
	{
		int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;
		HeapDataType* newNode = (HeapDataType*)realloc(php->data, sizeof(HeapDataType) * newcapacity);
		if (newNode == NULL)
		{
			perror("realloc");
			exit(-1);
		}
		php->data = newNode;   
		php->capacity = newcapacity;
	}
	php->data[php->size] = x;
	php->size++;
	AdjustUp(php->data, php->size - 1);
}

HeapDataType HPTop(HP* php)
{

	assert(php);
	return php->data[0];
}

void AdjustDown(HeapDataType* data, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && data[child+1] < data[child])
		{
			child++;
		}
		if (data[child] < data[parent])
		{
			Swap(&data[child], &data[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}


void HPPop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	Swap(&php->data[0], &php->data[php->size-1]);
	php->size--;
	AdjustDown(php->data, php->size, 0);
}

bool HPEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}



int main()
{
	int a[] = { 60,70,65,50,32,100 };

	HP hp;
	HPInit(&hp);
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		HPPush(&hp, a[i]);
	}

	while (!HPEmpty(&hp))
	{
		printf("%d ", HPTop(&hp));
		HPPop(&hp);
	}

	HPDestroy(&hp); 

	return 0;
}

代码测试

二叉堆性能：堆是为了实现排序而实现的一种数据结构，它并不是面向查找操作的，因为在堆中查找一个节点需要进行遍历，其平均时间复杂度是O(n)

不过在 插入 或 删除 某个值 和求二叉树中最值 往往具有很强的高效性

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1502435.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

selenium常用操作汇总

selenium常用操作汇总

本文总结使用selenium进行web/UI自动化时&#xff0c;会用到的一些常用操作。 定位元素 driver.find_element_by_xpath()#1、绝对路径 2、元素属性 3、层级和属性结合 4、使用逻辑运算符 driver.find_element_by_id()#根据id定位&#xff0c;HTML规定id属性在HTML文档中必须是唯…
阅读更多...
Mysql -- 约束

Mysql -- 约束

注意:约束是作用于表中字段上的,可以在创建表/修改表的时候添加约束. -- ------------------------------------------------------------------- 约束演示 ---------------------------------------------- create table user(id int primary key auto_increment comment 主键…
阅读更多...
CorelDRAW Standard2024适合业余爱好者和家庭企业的图形设计软件

CorelDRAW Standard2024适合业余爱好者和家庭企业的图形设计软件

CorelDRAW Standard 2024是一款功能强大的矢量图形设计软件&#xff0c;专为图形爱好者、家庭用户、微型企业和学生们设计。该软件在Windows平台上运行&#xff0c;并提供了智能对象、布局、插图和模板等功能&#xff0c;帮助用户快速创建高质量的设计作品。 CorelDRAW Standa…
阅读更多...
seq2seq翻译实战-Pytorch复现

seq2seq翻译实战-Pytorch复现

&#x1f368; 本文为[&#x1f517;365天深度学习训练营学习记录博客 &#x1f366; 参考文章&#xff1a;365天深度学习训练营 &#x1f356; 原作者&#xff1a;[K同学啊 | 接辅导、项目定制]\n&#x1f680; 文章来源&#xff1a;[K同学的学习圈子](https://www.yuque.com/…
阅读更多...
ssm+vue的农业信息管理系统（有报告）。Javaee项目，ssm vue前后端分离项目。

ssm+vue的农业信息管理系统（有报告）。Javaee项目，ssm vue前后端分离项目。

演示视频&#xff1a; ssmvue的农业信息管理系统&#xff08;有报告&#xff09;。Javaee项目&#xff0c;ssm vue前后端分离项目。 项目介绍&#xff1a; 采用M&#xff08;model&#xff09;V&#xff08;view&#xff09;C&#xff08;controller&#xff09;三层体系结构&…
阅读更多...
备考银行科技岗刷题笔记（持续更新版）

备考银行科技岗刷题笔记（持续更新版）

银行考试计算机部分复习 IEEE 802.11的帧格式 1.1 IEEE 802.11是什么&#xff1f; 802.11是国际电工电子工程学会&#xff08;IEEE&#xff09;为无线局域网络制定的标准。目前在802.11的基础上开发出了802.11a、802.11b、802.11g、802.11n、802.11ac。并且为了保证802.11更…
阅读更多...
npm install没有创建node_modules文件夹

npm install没有创建node_modules文件夹

问题记录 live-server 使用时 报错&#xff1a;live-server : 无法将“live-server”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。 npm install 安装 但是 这时npm install没有创建node_modules文件夹&#xff0c;只生成package-lock.json文件 方法一&#xff1a; 手…
阅读更多...
NineData与OceanBase完成产品兼容认证，共筑企业级数据库新生态

NineData与OceanBase完成产品兼容认证，共筑企业级数据库新生态

近日&#xff0c;云原生智能数据管理平台 NineData 和北京奥星贝斯科技有限公司的 OceanBase 数据库完成产品兼容互认证。经过严格的联合测试&#xff0c;双方软件完全相互兼容、功能完善、整体运行稳定且性能表现优异。 此次 NineData 与 OceanBase 完成产品兼容认证&#xf…
阅读更多...
软考70-上午题-【面向对象技术2-UML】-UML中的图1

软考70-上午题-【面向对象技术2-UML】-UML中的图1

一、图的定义 图是一组元素的图形表示&#xff0c;大多数情况下把图画成顶点、弧的联通图。 顶点&#xff1a;代表事物&#xff1b; 弧&#xff1a;代表关系。 可以从不同的角度画图&#xff0c;UML提供了13种图&#xff1a;&#xff08;只看9种&#xff09; 类图&#xff…
阅读更多...
学习c语言：顺序表

学习c语言：顺序表

一、顺序表的概念和结构 1.1 线性表 线性表&#xff08; linearlist &#xff09;是n个具有相同特性的数据元素的有限序列。线性表是⼀种在实际中⼴泛使⽤的数据结构&#xff0c;常⻅的线性表&#xff1a;顺序表、链表、栈、队列、字符串... 线性表在逻辑上是线性结构&#x…
阅读更多...
【网站项目】096实验室开放管理系统

【网站项目】096实验室开放管理系统

&#x1f64a;作者简介&#xff1a;拥有多年开发工作经验&#xff0c;分享技术代码帮助学生学习&#xff0c;独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。&#x1f339;赠送计算机毕业设计600个选题excel文件&#xff0c;帮助大学选题。赠送开题报告模板&#xff…
阅读更多...
15-单片机烧录FreeTOS操作系统后，程序的执行流程

15-单片机烧录FreeTOS操作系统后，程序的执行流程

任务创建 1、在系统上电后&#xff0c;第一个执行的是启动文件由汇编语言编写的复位函数 通过复位函数来初始化系统的时钟&#xff0c;然后再执行__main,初始化系统的堆和栈&#xff0c;然后跳转到main函数 2、在main函数中可以直接进行任务创建操作 因为在FreeRTOS中会自动…
阅读更多...
c++ primer plus 第十五章笔记 友元，异常和其他

c++ primer plus 第十五章笔记 友元，异常和其他

友元类&#xff1a; 两个类不存在继承和包含的关系&#xff0c;但是我想通过一个类的成员函数来修改另一个类的私有成员和保护成员的时候&#xff0c;可以使用友元类。 class A {private:int num;//私有成员//...public: //...friend class B;//声明一个友元类 }class…
阅读更多...
SpringBootWeb（接收请求数据，返回响应结果，分层解耦，Spring的IOCDI）【详解】

SpringBootWeb（接收请求数据，返回响应结果，分层解耦，Spring的IOCDI）【详解】

目录 一、接收请求数据 1. 接收表单参数 1.原始方式【了解】 2.SpringBoot方式 3.参数名不一致RequestParam 2.实体参数 1.简单实体对象 2.复杂实体对象 3.数组集合参数 4.日期参数 3. JSON参数 1.Postman发送JSON数据 2.服务端接收JSON数据 4. 路径参数(rest风格…
阅读更多...
httprunner结合pytest的关键字

httprunner结合pytest的关键字

1. 通用关键字 可参考官方文档&#xff1a; Write Testcase - HttpRunner V3.x Docs 2. 特别关键字 2.1. 步骤step前置 2.1.1. setup_hook 关键源码 def setup_hook(self, hook: Text, assign_var_name: Text None) -> "RunRequest":if assign_var_name:sel…
阅读更多...
【Python】新手入门：全局变量和局部变量的概念、区别以及用法

【Python】新手入门：全局变量和局部变量的概念、区别以及用法

【Python】新手入门&#xff1a;全局变量和局部变量的概念、区别以及用法 &#x1f308; 个人主页&#xff1a;高斯小哥 &#x1f525; 高质量专栏&#xff1a;Matplotlib之旅&#xff1a;零基础精通数据可视化、Python基础【高质量合集】、PyTorch零基础入门教程&#x1f448;…
阅读更多...
基于卷积神经网络的野外可食用植物分类系统

基于卷积神经网络的野外可食用植物分类系统

温馨提示&#xff1a;文末有 CSDN 平台官方提供的学长 QQ 名片 :) 1. 项目简介 本文详细探讨了一基于深度学习的可食用植物图像识别系统。采用TensorFlow和Keras框架&#xff0c;利用卷积神经网络&#xff08;CNN&#xff09;进行模型训练和预测&#xff0c;并引入迁移学习模型…
阅读更多...
联立方程模型的可识别性的通俗解释

联立方程模型的可识别性的通俗解释

联立方程模型的可识别性&#xff0c;主要的解法是阶条件算法和秩条件算法&#xff0c;数学公式角度的解释就不讲了&#xff0c;参考下面的前人文献。 【计量经济学】联立方程模型-CSDN博客 说一下公式算法背后的通俗原理。 在计量经济模型中&#xff0c;比如 Y23*Xu中&#x…
阅读更多...
springboot251基于springboot-vue的毕业论文管理系统

springboot251基于springboot-vue的毕业论文管理系统

毕业论文管理系统设计与实现 摘 要 现代经济快节奏发展以及不断完善升级的信息化技术&#xff0c;让传统数据信息的管理升级为软件存储&#xff0c;归纳&#xff0c;集中处理数据信息的管理方式。本毕业论文管理系统就是在这样的大环境下诞生&#xff0c;其可以帮助管理者在短…
阅读更多...
实战｜环信 Vue2 uniapp Demo重构焕新！经典再升级！

实战｜环信 Vue2 uniapp Demo重构焕新！经典再升级！

项目背景 当前环信 uni-app vue2 Demo 地址升级版本 Github 地址&#xff08;临时&#xff09; 原版本功能实现方式较混乱&#xff0c;代码逻辑晦涩难懂&#xff0c;不利于开发者参考或复用。此实战项目在确保原项目功能保留的情况下进行完全重写并新增大量功能&#xff0c;以…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023