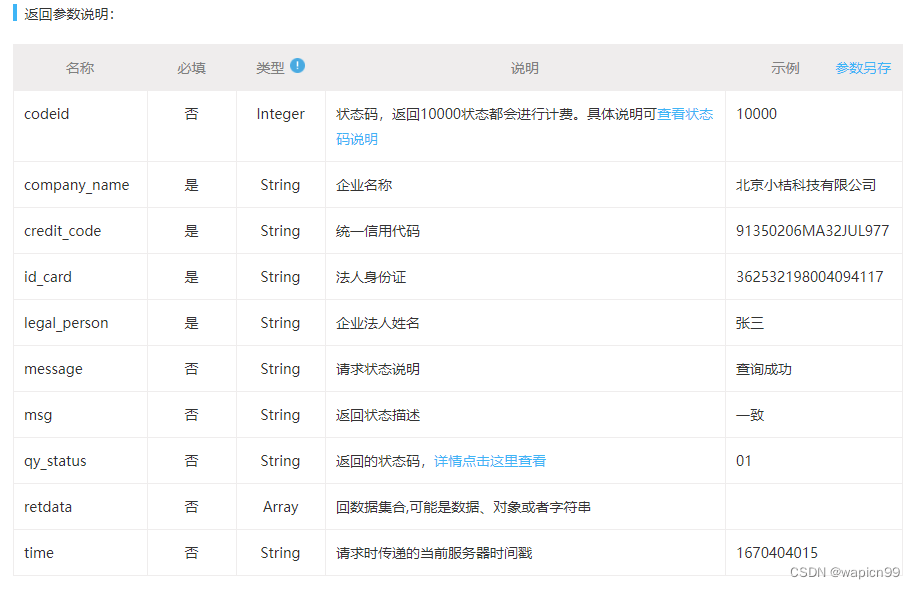
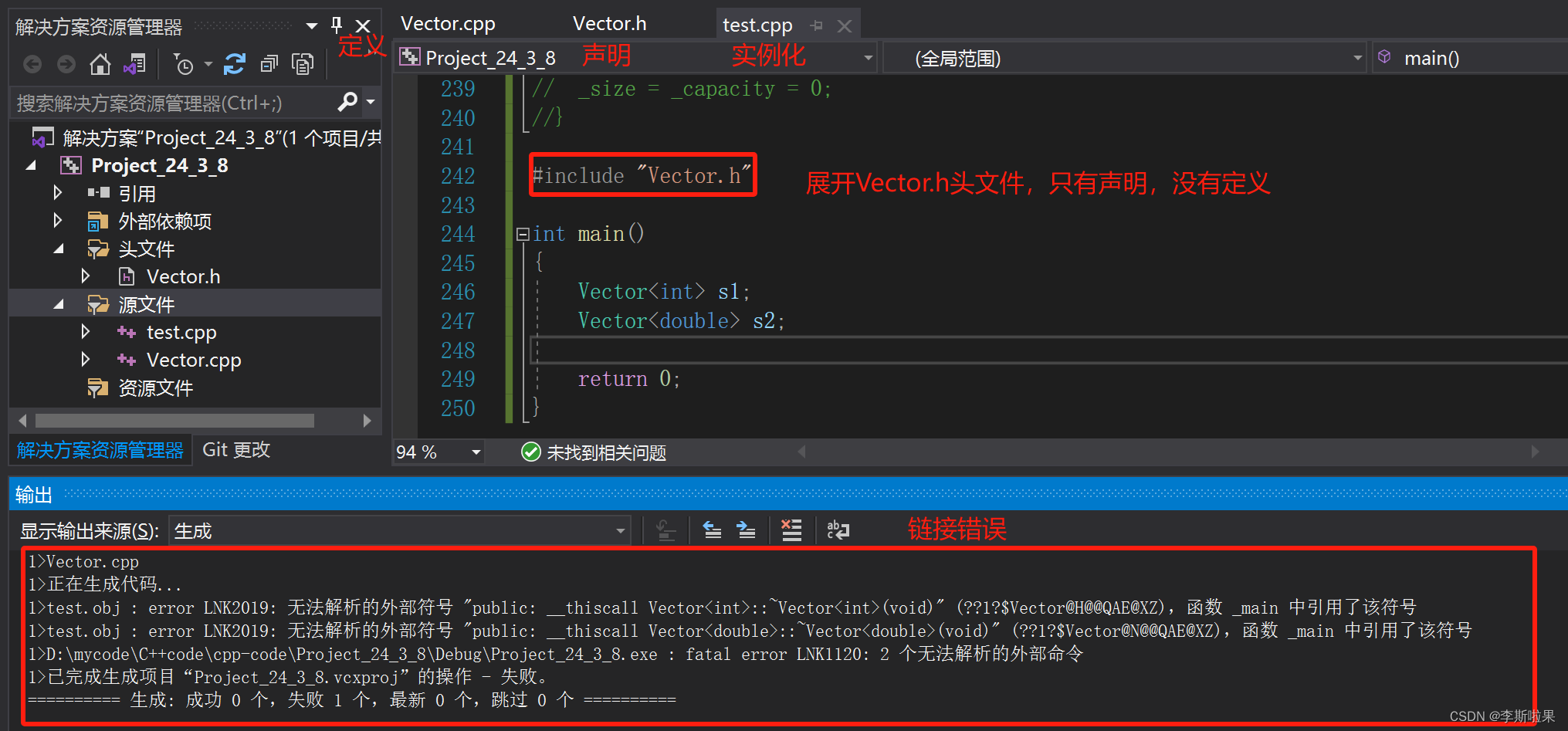
联立方程模型的可识别性，主要的解法是阶条件算法和秩条件算法，数学公式角度的解释就不讲了，参考下面的前人文献。

【计量经济学】联立方程模型-CSDN博客

说一下公式算法背后的通俗原理。

在计量经济模型中，比如 Y=2+3*X+u中，实际上 X 被视为“会变的已知数”，Y是“未知数”，我们在用X求解Y。

这意味着，我们只能用一个方程 Y=2+3*X 来求解Y，如果又给我们一个方程说 Y=4+5*X，这时就意味着，我们无法通过 X 求出 Y 了，因为两个方程矛盾（注意，你可能会问，两个方程不是正好将X和Y两个变量求出来吗？但你问的是初等数学中求定值变量的思维，在计量经济学中 X 是一个“会变的已知数”而不是一个“固定的已知数”。所以说，两个方程中只有一个待求变量 Y，而X是一个已知数）。这就是联立方程模型求解的通俗原理。

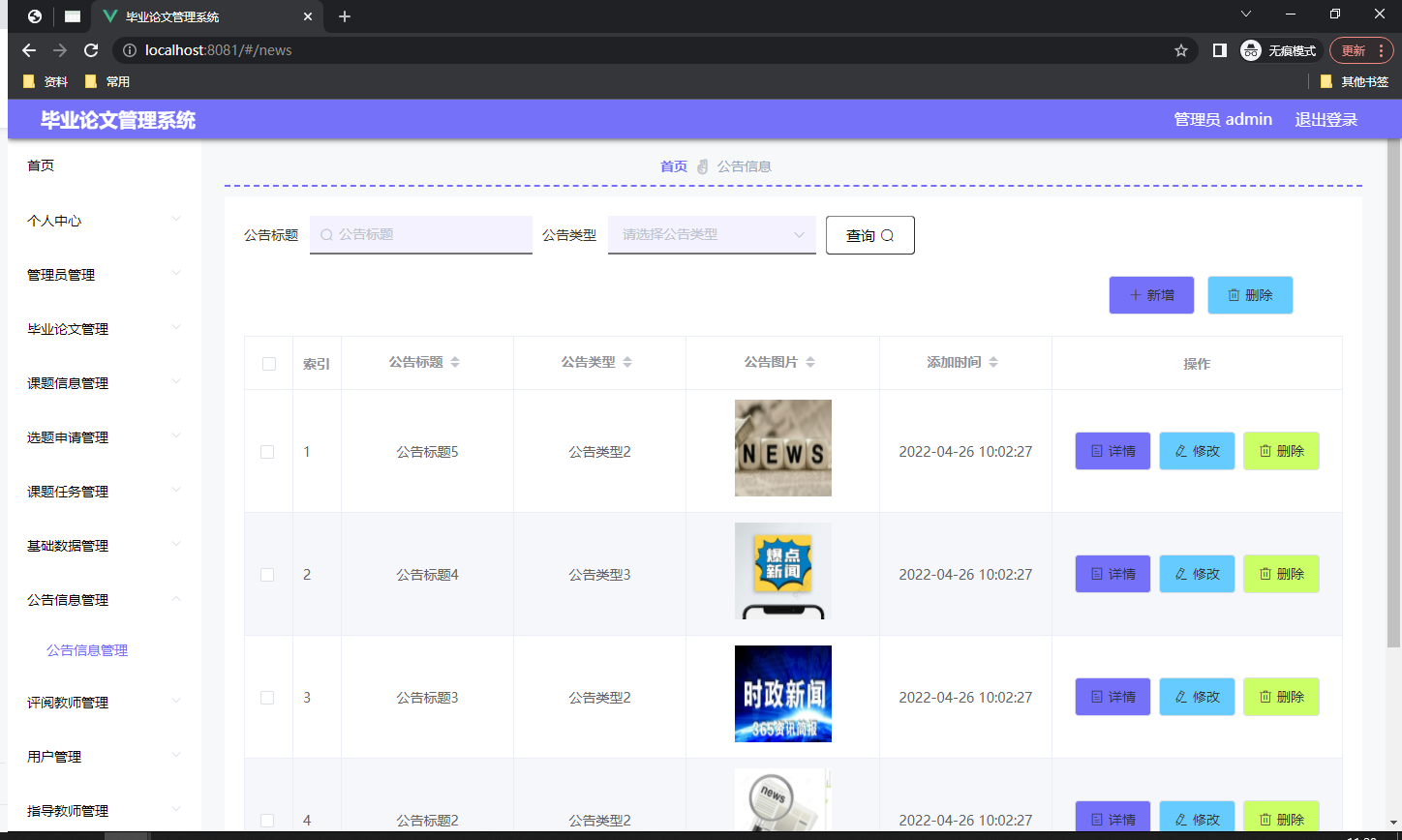
从网上随手搜索到下面这个题，咱们来看看第一个方程的可识别性。

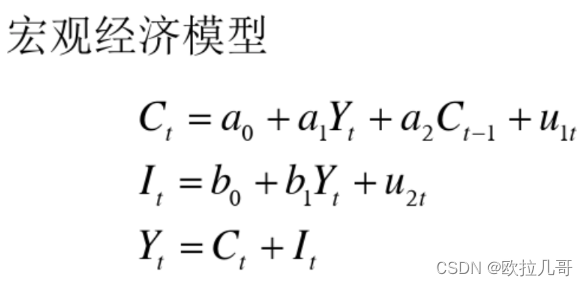
我们将第二个方程带入第三个方程，消掉 I 后整理得到 C=-b0+(1-b1)*Y-u2，即 C 由 Y 决定。然而，第一个方程又规定了 C=a0+a1*Y+a2*C(t-1)+u2，它是在说 C 由 Y 和 C(t-1) 决定。

换句话说，当我们面对 C=-2+3*Y 和 C=4+5*Y+6*C(t-1) 两个方程时，是根本就不出来 C 的，因为两个方程是矛盾的，因为 Y 和 C(t-1) 都是“会变的已知数”，而且两者都是自由改变，不存在Y受到C(t-1)制约的情况（也就是二者不存在线性相关性）。

你可能会说两个方程可以消掉C得到 Y = a+b* C(t-1) 的形式啊，这不是说明有解吗？其实这是不对的，因为前面已经说了：Y 和 C(t-1) 都是“会变的已知数”，而且两者都是自由改变，不存在Y受到C(t-1)制约的情况（也就是二者不存在线性相关性）。而你得到的  Y = a+b* C(t-1) 意味着Y不是只有变化的，而是在受 C(t-1) 的约束。

明白了上面一个自然段的道理，就不要再问：针对 C=-2+3*Y 和 C=4+5*Y+6*C(t-1) 可以先消掉 Y 从而得到 C=a+b*C(t-1) 的形式进行求解啊？不要再问了，因为在消掉 Y 的过程中，Y 已经不再是一个 “可以只有改变的已知数” 了。隐含之中，Y 已经被 C(t-1) 得的死死的了，也就是 Y 与 C(t-1) 强相关。

以上内容，有些点需要初学者再多思考思考，才能理解联立方程模型的可识别性问题。