在刷题中，遇到这样两道类似知识点的题目，下面是两道题的链接，感兴趣的朋友可以去尝试一下。力扣链接: 快乐数力扣链接: 环形链表。

一、鸽巢原理

这两道题都用到这样的一个知识点–鸽巢原理，也叫抽屉原理

鸽巢原理（Pigeonhole Principle）是一种基本的数学原理，通常用于证明存在性问题。该原理的核心思想是：如果有更多的物品（例如鸽子）要放入比可用的位置（巢）更少的容器中，则至少会有一个容器中放入了多个物品。换句话说，如果将n+1个或更多的物品放入n个容器中，则至少有一个容器中至少有两个物品。
这个原理在解决许多数学问题时非常有用，包括组合数学、图论、概率论等领域。它经常被用来证明某些对象的存在性，而不需要给出具体的构造或描述。

用简明的话来讲，就是有N个鸽子巢穴，有N+1个鸽子，那么必定有一个巢穴的有2个以上的鸽子。

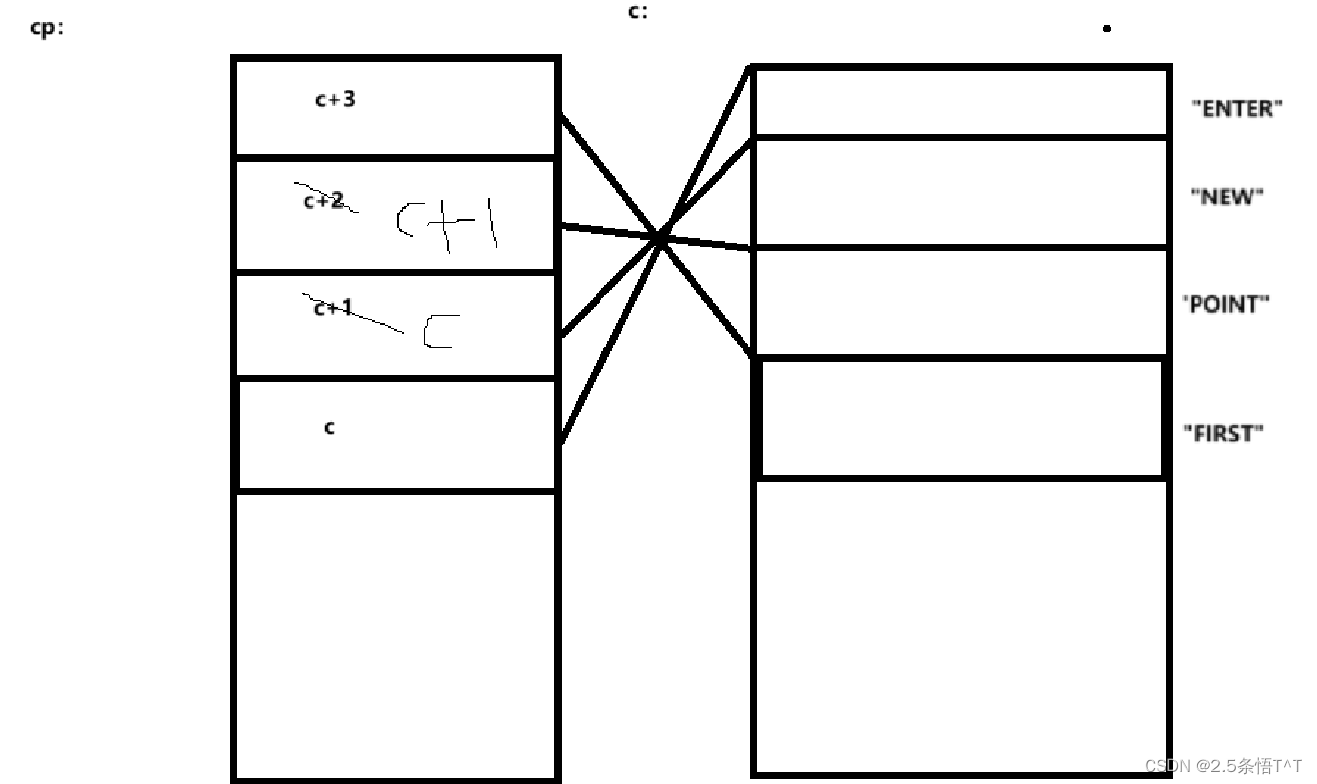
二、环的入口点

分析题目

题目要中有两个要素需要我们去做：
1.判断是否有环
2.若有环，求出入口点

思路

首先我们要判断是否有环
采用快慢双指针的思想，定义一个快指针和慢指针，每次快指针走两步，满指针走一步为什么快指针走两步，慢指针走一步呢？不能快指针走三步，四步，慢指针走两步三步吗？原因如下

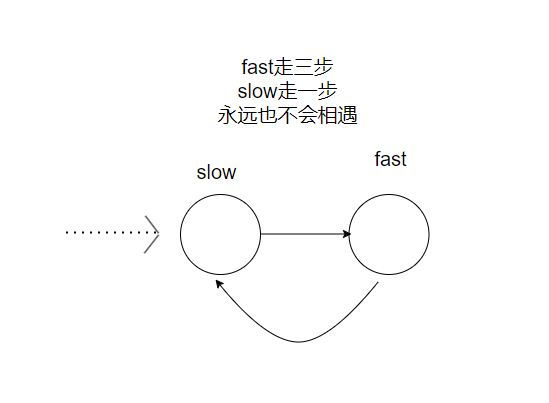
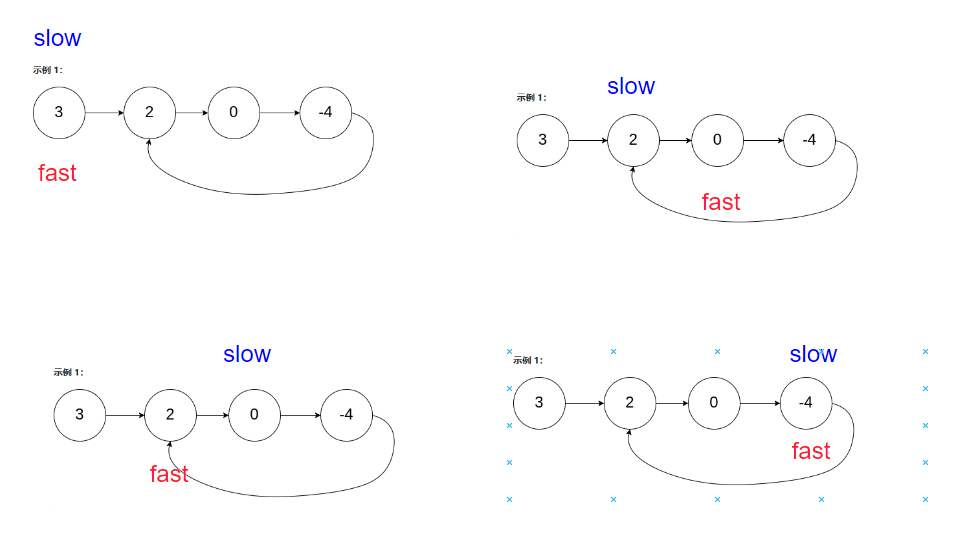
判断出链表有环
判断出链表有环之后，我们就要寻找入口点了

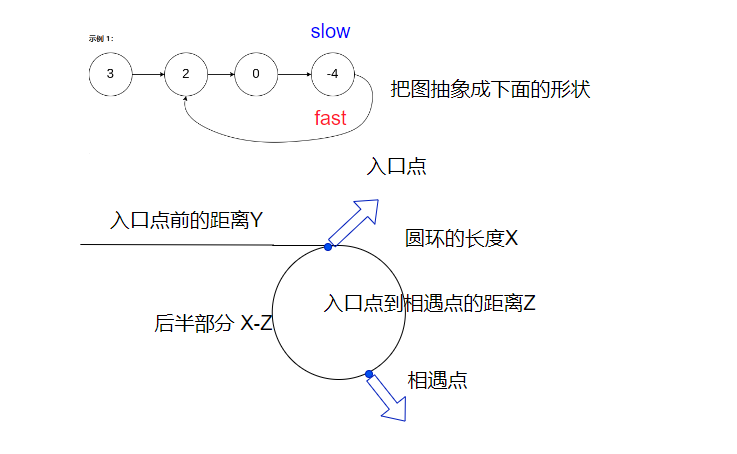
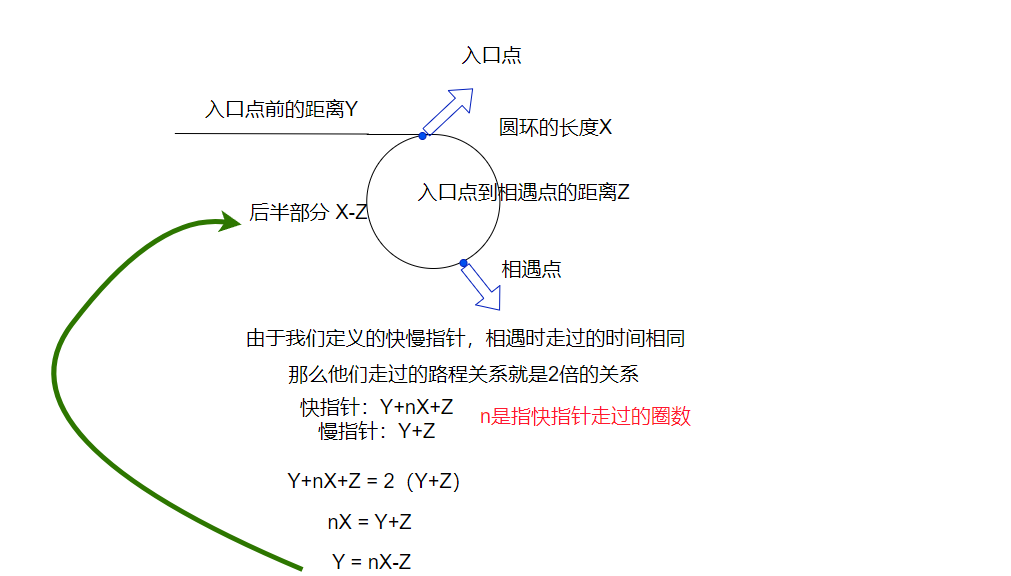
代码

public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null || head.next == null){
            return null;
        }
           ListNode slow = head;
           ListNode fast = head;
           while (fast!=null && fast.next != null){
               fast = fast.next.next;
               slow = slow.next;
               if (slow == fast){
                   break;
               }
           }
           if (fast == null || fast.next==null){
               return null;
           }
           slow = head;
           while (slow != fast){
               slow  = slow.next;
               fast = fast.next;
           }
           return slow;

    }
}

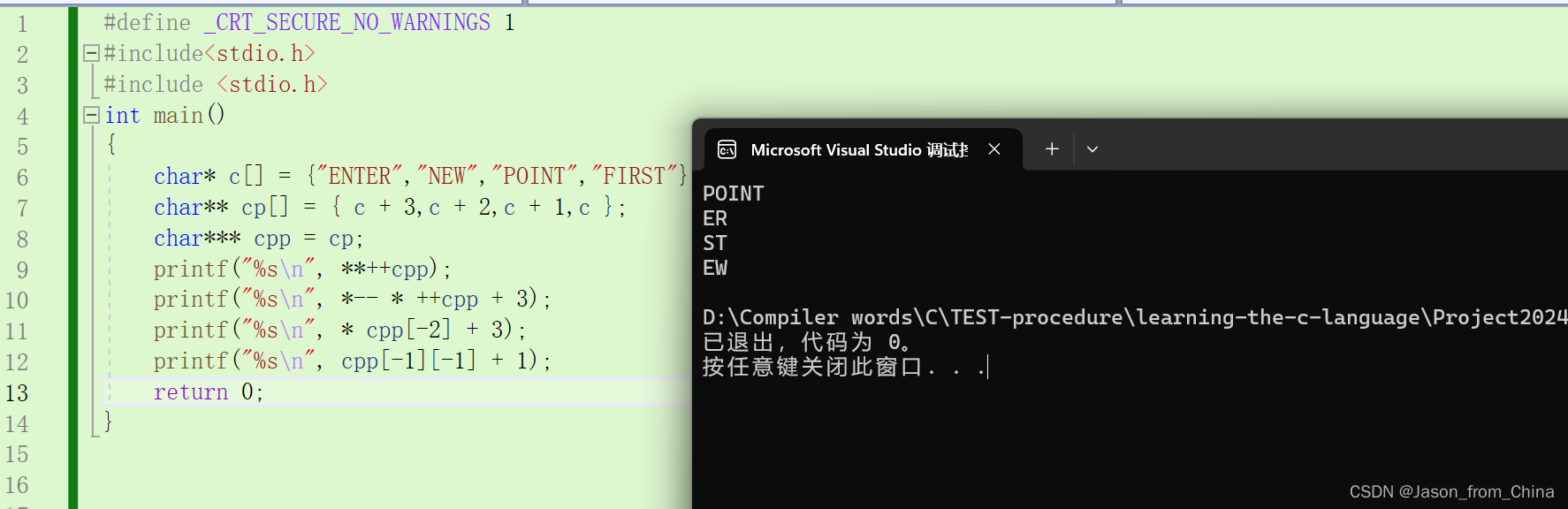
三、快乐数

分析题目

这里是题目表述，题目虽然是简单类型，但也要搞清楚为什么可以这样做，才是刷题的根本。
单看题目描述可能不太直观，这里是案例，帮助大家理解题目

这个题最精髓的地方在于搞懂无限循环。这也是写这道题解的原因。
其中题目给出了n的取值范围。 1 <= n <= 2,147,483,647

思路

我们先梳理思路，给出一个数，我们按照题目要求，计算每一位的平方的和，与1判断，如果不相等，则再次重复操作。
那么我们怎么能知道这个数，是不是一在无限循环呢？
这里就用到鸽巢原理了。

当重复的数不是1时，我们就退出，说明不是快乐数
因为当重复的数字不是1时，他们往后的操作的值一定相等，最后重复的还是这个数字。

由分析题目可以得出，这个数字一定会重复，所以我们只要判断重复的数字是不是为就可以。
所以我们可以采用快慢双指针的思想来进行代码的书写。
具体思路：定义一个快指针，每次走两步，定义一个慢指针，每次走一步，当两个指针的值相等时，判断是否为。

代码

 public int func(int n){//计算每位平方的和的函数
        int sum = 0;
        while (n > 0){
            int temp = n%10;
            sum += temp*temp;
            n = n/10;
        }
        return sum;
    }
    public boolean isHappy(int n) {
           int slow = n;//慢指针
           int fast = func(n);//快指针
           while (slow != fast){//循环的条件
               slow = func(slow);//走一步
               fast = func(func(fast));//走两步
           }
           return fast == 1;//判断条件
    }

以上就是所有内容，如果对你有帮助的话，点赞关注支持一波吧！