Mindopt 是一个优化求解器,如果它有两个主要版本——0.xx和1.x.x(最新版本1.1.1),它们代表着软件开发的两个不同阶段。版本1.0.0表示软件的一个大的里程碑,代表着软件第一个正式的“成熟”发布版本,而0.25是一个较早期的开发版本。在这篇博客中,我们将把这个最新版本与它的前身0.25版进行比较。
简介
Mindopt是一款高性能优化求解器,专为解决从简单线性规划 (LP) 到更复杂的混合整数规划 (MIP) 、非线性规划(QP、SDP)的一系列问题而设计。其强大的算法旨在有效地找到最佳解决方案,使其成为运筹学,电力能源、工业制造、交通物流和其他领域的研究人员和专业人员的首选工具。
版本0.25与1.1.1之间API的差异
功能差异:
1.1.1版本的API引入一些新的功能和参数选项,这些功能可能在0.25版本中不可用。例如,1.1.1版本增加一些高级优化算法、并行计算支持、更强大的约束处理能力等功能,这些功能可能并不在0.25版本的API中存在。例如:新增 MILP 的热启动(warm start) 和SOS约束和Indicator约束,新增回调函数功能 (Callback),输入文件增加支持.qps格式,提供了线性规划问题的 primal-dual feasible solution.改进并发优化方法 (concurrent optimization method) 的算法流程等等。
- 新增:callback回调功能
- 可用于获取中间结果,进行求解过程跟踪;
- 也可设置启发式决策来优化求解速度,比如:添加割平面,裁剪不会出现最优解的分支;干预 MindOpt 的分支选择策略,控制节点二分方法及遍历顺序;添加自定义可行解(比如通过某种启发式算法得到),一个较好的可行解可以加速 MindOpt 的求解效率。
接口设计:
1.1.1版本的API对接口进行重新设计,以提高灵活性和可定制性。这导致一些方法的名称、参数数量或参数类型发生变化。例如支持定义变量的类型、定义约束时支持使用等式符号等等。例如:
- 添加变量和约束
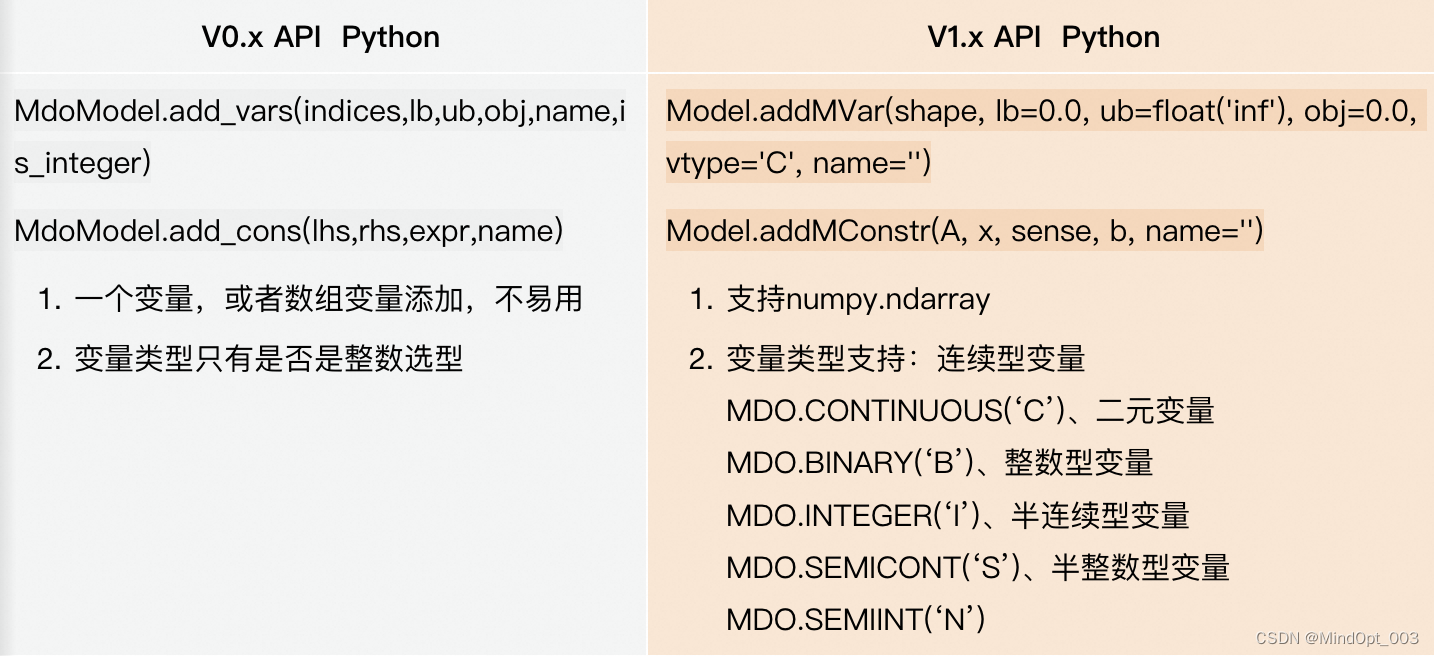
示例:
- 1.1.1版本
38 # Add variables.
39 x = []
40 x.append(model.addVar(0.0, 10.0, 1.0, 'I', "x0"))
41 x.append(model.addVar(0.0, float('inf'), 2.0, 'I', "x1"))
42 x.append(model.addVar(0.0, float('inf'), 1.0, 'I', "x2"))
43 x.append(model.addVar(0.0, float('inf'), 1.0, 'C', "x3"))
- 0.25版本
41 # Add variables.
42 x = []
43 x.append(model.add_var(0.0, 10.0, 1.0, None, "x0", True))
44 x.append(model.add_var(0.0, MDO_INFINITY, 1.0, None, "x1", True))
45 x.append(model.add_var(0.0, MDO_INFINITY, 1.0, None, "x2", True))
46 x.append(model.add_var(0.0, MDO_INFINITY, 1.0, None, "x3", False))
- 设置目标

性能差异:
由于0.25版本停止更新,而1.1.1作为正式版本会持续对算法进行优化和改进,因此其在性能方面会持续提升。这会导致一些API方法的响应时间、收敛速度等方面的差异越来越大。
一个完整的示例:
代码如下:
from mindoptpy import *
import time
import numpy as np
if __name__ == "__main__":
# 声明参数和集合
plant = ["小麦","玉米","蔬菜","瓜果"]
plant_ub = [76,88,40,96]
field = ["地块1","地块2","地块3","地块4","地块5","地块6"]
field_ub = [42, 56, 44, 39, 60, 59]
profit_plant_field =np.array([
[500 ,550 ,630 ,1000 ,800 ,700],
[800 ,700 ,600 ,950 ,90 ,930],
[1200 ,1040 ,980 ,860 ,880 ,780],
[1000 ,960 ,840 ,650 ,600 ,700]
])
alt_plant = [1,1,1,1] # for矩阵相乘得到加和
alt_field = [1,1,1,1,1,1] # for矩阵相乘得到加和
# Step 1. Create a model and change the parameters.
model = Model(name = 'LP_1_plant2')
try:
# Step 2. Input model.
# Change to maximize problem.
model.modelsense = MDO.MAXIMIZE
# Add variables.
#vars = {}
vars = model.addMVar((len(plant),len(field)), obj=profit_plant_field, vtype='C', name="x")
# Add constraints.
#cons = {}
constrs1 = model.addConstr( alt_plant @ vars <= 0)
constrs1.rhs = field_ub
constrs1.lhs = 0
constrs2 = model.addConstr( vars @ alt_field <= 0)
constrs2.rhs = plant_ub
constrs2.lhs = 0
# Step 3. Solve the problem and populate the result.
model.optimize()
time.sleep(1) #for print
model.write("model/plant2.lp") #可以输出文件,观察建模是否正确
model.write("model/plant2.sol")
if model.Status == MDO.OPTIMAL:
print("----\n")
print(f"目标函数是: {model.objval}")
print("决策变量:")
x = vars.X
print(x)
for p in range(len(plant)):
for f in range(len(field)):
if x[p,f] != 0:
print("{0}在{1}的种植面积≈{2:.0f}".format(plant[p],field[f],x[p,f]))
else:
print("无可行解!求解结束状态是:(code {0}).".format(model.Status))
except MindoptError as e:
print("Received Mindopt exception.")
print(" - Code : {}".format(e.code))
print(" - Reason : {}".format(e.message))
except Exception as e:
print("Received other exception.")
print(" - Reason : {}".format(e))
finally:
# Step 4. Free the model.
model.dispose()
此案例可在云上平台查看运行结果,也可对案例复制调试。
相同案例不同代码的对比:1.xx版本vs0.xx版本