文章目录
- BASICS
- strcutural Inception
- 算法思想
- 算法核心
- 算法架构
- Re-Parameter四部曲:ACNet
- ACNet原理
- ACNet分析
- 涨点原因
- 推理阶段融合机制
- Re-Parameter四部曲:RepVGG
- RepVGG原理
- RepVGG分析
- RepVGG Block
- Structural Re-Parameters
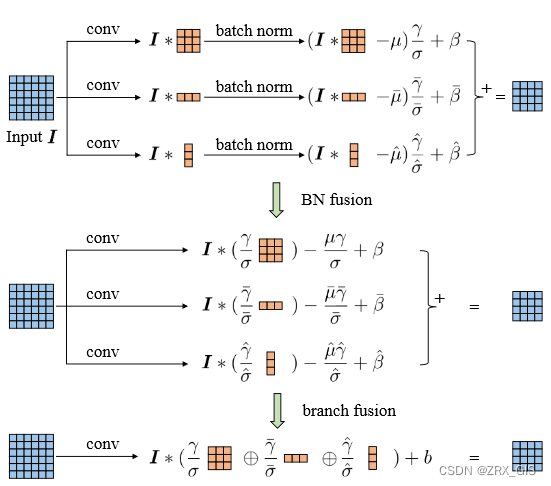
- 融合conv2d和BN
- 融合1x1conv转换为3x3conv
- 将BN转换为3x3conv
- 多分支融合
- Re-Parameter四部曲:Diverse Branch Block
- 六种转换方法
- a conv for conv-BN
- a conv for branch addition
- a conv for sequential convolutions
- a conv for depth concatenation
- a conv for average pooling
- a conv for multi-scale convolutions
- DBB分析
- Re-Parameter四部曲:OREPA
- RepVGG原理
- Online Re-Parameterization
- 重参数中的归一化
- 模块线性表达(Block Linearization)
- Block Squeezing
- 多分支拓扑结构的梯度分析
BASICS
strcutural Inception
Inception架构由Google提出,常规包括Ixception-V1、Ixception-V2、Ixception-V3、Ixception-V4、Ixception-ResNet,版本间差异主要集中在迭代方式上,这里我们以V1为例子,介绍Ixception的结构特点。论文地址
算法思想
对于CNN来说,提升网络性能最好的方式是增加网络的深度和维度,对于深度而言,就是我们常说的将数据集下采样至8倍、16倍、32倍等等;维度便是特征图所包含的通道数。如果我们将改进的点放置在这种方式上,那么会存在一个问题,即参数呈指数倍上涨,并且随着parameter的不断增加,网络所诱发的过拟合现象出现的概率也会随之提高。Inception结构的产生便是针对这一问题,Inception的算法基础思想来源于网络中的网络(Network in Network)和稀疏网络架构,产生则是在GoogLeNet。
算法核心
Inception实质是将全连接甚至一般的卷积结构都转化为稀疏连接,将稀疏矩阵聚类为较为密集的子矩阵来提高计算性能。
算法架构
Inception是一类较为早期的CNN结构,因此模块并不复杂,结构上包含三次conv和一次max_pooling,这种操作在当前的研究中也经常被使用,比如ASPP,他们实质上是想丰富特征图的多尺度信息。作者在对模块设计上的解释大概意思是:当期望焦点分布区域全局化时,大conv_kernel的特征会更加丰富,反之,小conv_kernel的特征会更令人满意。
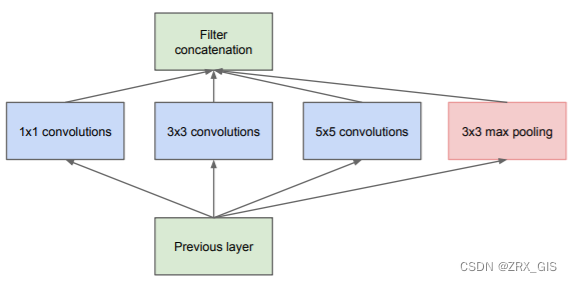
当然,仅上图的结构并不能支撑Inception封神,在此基础上,Inception还有一个降维版本(dimension reductions),相比较而言,降维版的使用不同尺寸的卷积核可以提取到种类更加丰富的特征,同时,使用稀疏矩阵分解为密集矩阵计算的原理,增加了收敛速度。
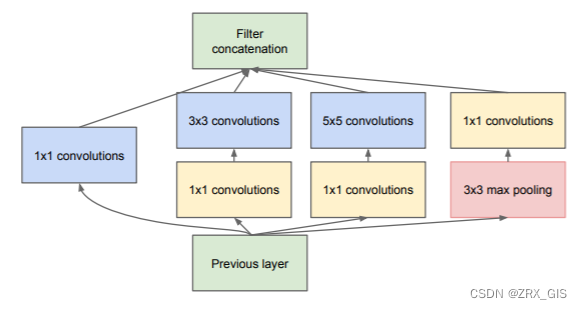
Re-Parameter四部曲:ACNet
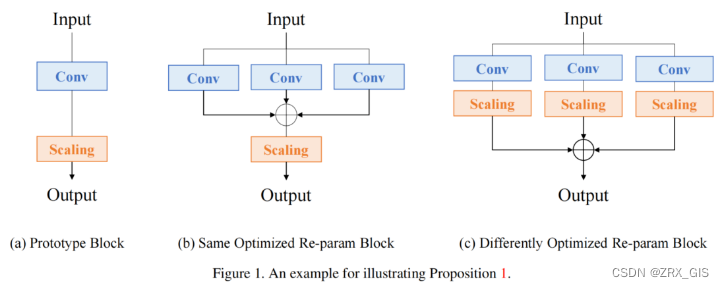
ACNet在Re-Parameters领域具有重要意义,论文地址,作者提出architecture-neutral结构,不对称卷积块(Asymmetric Convolution Block, ACB),文中指出,CNN定义为architecture-neutral前需要满足两点:首先,没有对特定的体系结构做任何假设;其次便是具备普适性。 ACB作为一种即插即用的结构,对于任意现有的模型,在训练阶段用ACB替换其中的方形卷积核,几乎都可以带来精度的提升,并且没有引入新的超参,无需额外的微调。在推理阶段,通过权重融合将ACB还原成模型原有的结构,这样既获得了精度提升又没有增加推理时间。
ACNet原理
宏观上来看「ACNet分为训练和推理阶段,训练阶段重点在于强化特征提取,实现效果提升。而测试阶段重点在于卷积核融合,不增加任何计算量」。
「训练阶段」:因为卷积是大多数网络的基础组件,因此ACNet的实验都是针对3x3卷积进行的。训练阶段就是将现有网络中的每一个3x3卷积换成1x3卷积+3x1卷积+3x3卷积共三个卷积层,最终将这三个卷积层的计算结果进行融合获得卷积层的输出。因为这个过程中引入的卷积和卷积是非对称的,所以将其命名为Asymmetric Convolution。
「推理阶段」:这部分主要是对三个卷积核进行融合。这部分在实现过程中就是使用融合后的卷积核参数来初始化现有的网络,因此在推理阶段,网络结构和原始网络是完全一样的了,只不过网络参数采用了特征提取能力更强的参数即融合后的卷积核参数,因此在推理阶段不会增加计算量。
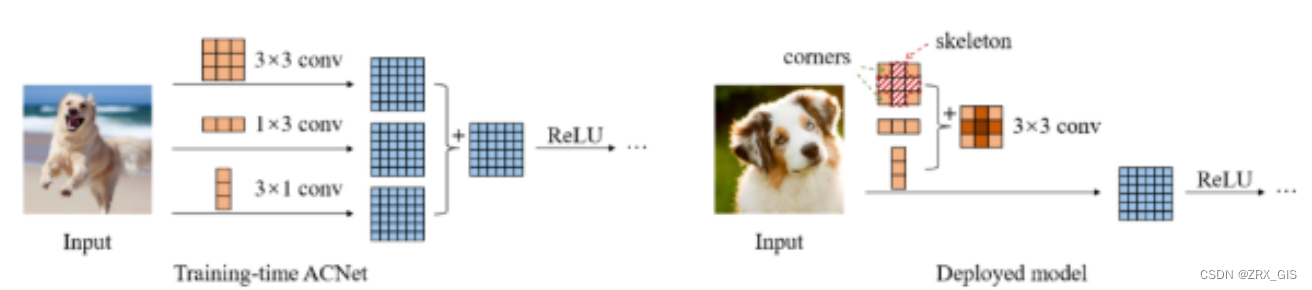
总结一下就是ACNet在训练阶段强化了原始网络的特征提取能力,在推理阶段融合卷积核达到不增加计算量的目的。虽然训练时间增加了一些时间,但却换来了在推理阶段速度无痛的精度提升。
ACNet分析
涨点原因
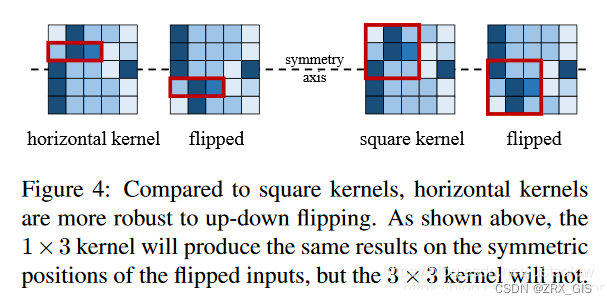
论文中提到,ACNet有一个特点是「它提升了模型对图像翻转和旋转的鲁棒性」,例如训练好后的1x3卷积和在图像翻转后仍然能提取正确的特征(如Figure4左图所示,2个红色矩形框就是图像翻转前后的特征提取操作,在输入图像的相同位置处提取出来的特征还是一样的)。那么假设训练阶段只用3x3卷积核,当图像上下翻转之后,如Figure4右图所示,提取出来的特征显然是不一样的。因此,引入1x3这样的水平卷积核可以提升模型对图像上下翻转的鲁棒性,竖直方向的3x1卷积核同理。
推理阶段融合机制
推理阶段的融合机制可能是大家最关系的一个问题,推理阶段的融合操作如Figure3所示,在论文中提到具体的融合操作是和BN层一起的,然后融合操作是发生在BN之后的。但是其实也可以把融合操作放在BN层之前,也就是三个卷积层计算完之后就开始融合。
Re-Parameter四部曲:RepVGG
论文地址,从名字上,我们就可以看出RepVGG是针对VGG来的。在VGG提出后,很多学者发现VGG在精度上比不过RestNet,在速度上比不过Moblienet,这无疑让VGG备受打击,并慢慢退出历史舞台。就在VGG快要销声匿迹时,咱们国内大佬(清华、港科技)和企业(旷视)联合提出RepVGG,希望在经典网络上再创辉煌。
RepVGG原理
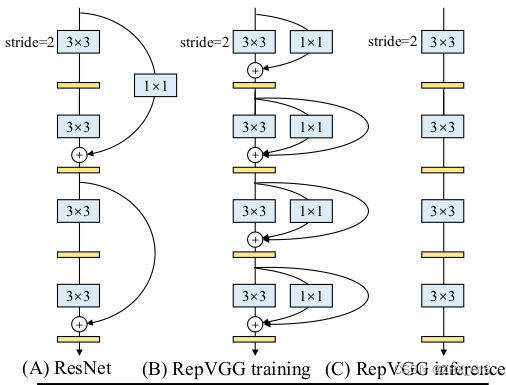
实际上就是在训练时,使用一个类似ResNet-style的多分支模型,而推理时转化成VGG-style的单路模型。如下图所示,图(B)表示RepVGG训练时所采用的网络结构,而在推理时采用图(C)的网络结构。关于如何将图(B)转换到图(C)以及为什么要这么做后面再细说,如果对模型优化部署有了解就会发现这和做网络图优化或者说算子融合非常类似。
RepVGG分析
RepVGG Block
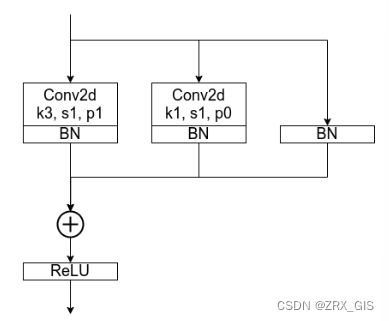
训练时RepVGG Block并行了三个分支:一个卷积核大小为3x3的主分支,一个卷积核大小为1x1的shortcut分支以及一个只连了BN的shortcut分支。这里首先抛出一个问题,为什么训练时要采用多分支结构。如果之前看过像Inception系列、ResNet以及DenseNet等模型,我们能够发现这些模型都并行了多个分支。至少根据现有的一些经验来看,并行多个分支一般能够增加模型的表征能力。所以你会发现一些论文喜欢各种魔改网络并行分支。接着再问另外一个问题,为什么推理时作者要将多分支模型转换成单路模型?七个字:更快、更小、更灵活。
Structural Re-Parameters
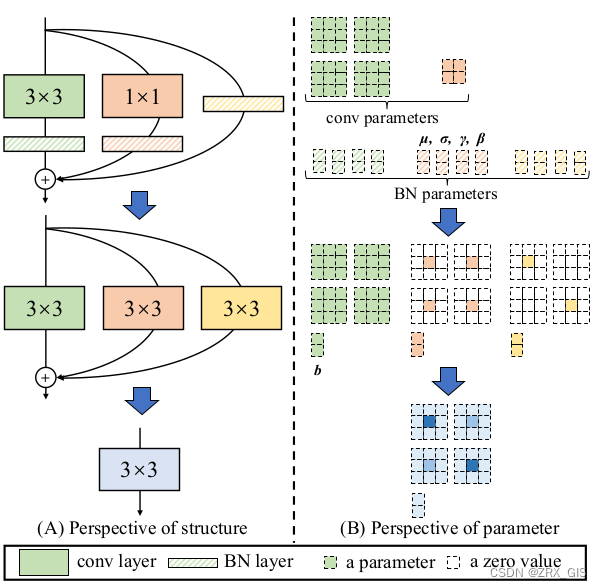
在简单了解RepVGG Block的训练结构后,接下来再来聊聊怎么将训练好的RepVGG Block转成推理时的模型结构,即structural re-parameterization technique过程。根据论文中的图4(左侧)可以看到,结构重参数化主要分为两步,第一步主要是将Conv2d算子和BN算子融合以及将只有BN的分支转换成一个Conv2d算子,第二步将每个分支上的3x3卷积层融合成一个卷积层。关于参数具体融合的过程可以看图中右侧的部分。
融合conv2d和BN
关于Conv2d和BN的融合对于网络的优化而言已经是基操了。因为Conv2d和BN两个算子都是做线性运算(线性运算是加法和数量乘法,对于不同向量空间线性运算一般有不同的形式,它们必须满足交换律,结合律,数量加法的分配律,向量加法的分配律),所以可以融合成一个算子。
融合1x1conv转换为3x3conv
这个过程比较简单,以1x1卷积层中某一个卷积核为例,只需在原来权重周围补一圈零就行了,这样就变成了3x3的卷积层。
将BN转换为3x3conv
对于只有BN的分支由于没有卷积层,所以我们可以先自己构建出一个卷积层来。构建了一个3x3的卷积层,该卷积层只做了恒等映射,即输入输出特征图不变。既然有了卷积层,那么又可以按照上述内容将卷积层和BN层进行融合。
多分支融合
这个其实也不难,合并的过程其实也很简单,直接将这三个卷积层的参数相加即可。
Re-Parameter四部曲:Diverse Branch Block
有了前两篇文章ACNet和RepVGG的铺垫,本文就忽略背景介绍,直接进入核心内容的讲解。本文首先总结了六种不同的结构重参数化的转换方法,然后借鉴Inception的多分支结构提出了一种新的building block:Diverse Branch Block(DBB),在训练阶段,对模型中的任意一个K×K 卷积,都可以用DBB替换,由于DBB引入了不同感受野、不同复杂度的多分支结构,可以显著提升原有模型的精度。在推理阶段,通过这六种结构重参数转换方法,可以将DBB等价地再转换成一个K×K 卷积,这样就可以在模型结构、计算量、推理时间都不变的前提下无损涨点。论文地址
六种转换方法
a conv for conv-BN
略(见上一部分)
a conv for branch addition
略(见上一部分)
a conv for sequential convolutions
这是本文新提出的一种转换类型同时也是最复杂的一种。这一转换是将连续的1x1 conv - BN - KxK conv - BN转换成一个单个的 K x K conv。
a conv for depth concatenation
Inception中是通过沿通道拼接的方式来融合多个分支的结果,当多个分支都只含有一个卷积层且规格相同的情况下,对多个分支的结果沿通道拼接等价于将每个分支的卷积核沿输出通道维度进行拼接,这里的输出维度就是每个卷积层的卷积核个数。
a conv for average pooling
平均池化可以等价为一个大小和步长相等的卷积
a conv for multi-scale convolutions
略(见ACNet)
DBB分析
一个完整的DBB block如下图所示,其中包含四个分支,通过上述六种转换,在推理阶段可以将其等价转换为一个卷积,因此对于任意现有的网络如ResNet等,在训练阶段可以将其中的 3×33×3 卷积替换成DBB block,推理阶段再转换回去,达到无损涨点的目的。
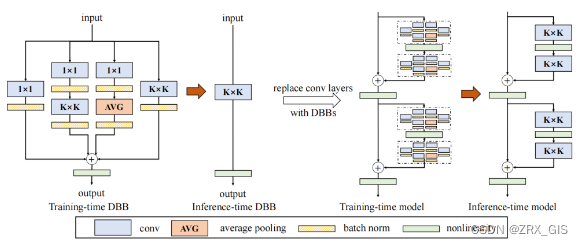
Re-Parameter四部曲:OREPA
论文提出了在线重参数方法OREPA,在训练阶段就能将复杂的结构重参数为单卷积层,从而降低大量训练的耗时。为了实现这一目标,论文用线性缩放层代替了训练时的BN层,保持了优化方向的多样性和特征表达能力。从实验结果来看,OREPA在各种任务上的准确率和效率都很不错。论文地址
RepVGG原理
Online Re-Parameterization
重参数中的归一化
作者认为中间BN层是重参化过程中多层和多分支结构的关键组成部分。以SoTA模型DBB和RepVGG为例,去除这些层会导致严重的性能下降,因此,作者认为中间的BN层对于重参化模型的性能是必不可少的。然而,中间BN层的使用带来了更高的训练预算。作者注意到,在推理阶段,重参化块中的所有中间操作都是线性的,因此可以合并成一个卷积层,从而形成一个简单的结构。但在训练过程中,BN层是非线性的,即它们将特征映射除以其标准差。因此,中间操作应该单独计算,这将导致更高的计算和内存成本。更糟糕的是,如此高的成本将阻止探索更强大的训练模块。
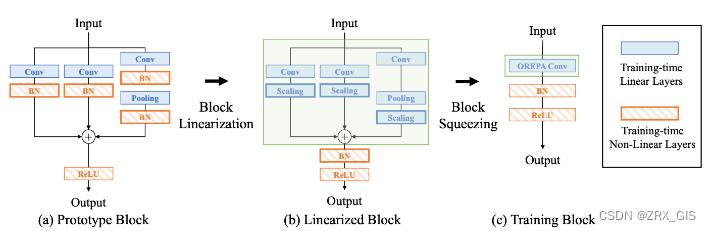
模块线性表达(Block Linearization)
中间的BN层阻止了在训练过程中合并单独的层。然而,由于性能问题,直接删除它们并不简单。为了解决这一困境,作者引入了channel级线性尺度操作作为BN的线性替代方法。缩放层包含一个可学习的向量,它在通道维度中缩放特征映射。线性缩放层具有与BN层相似的效果,它们都促进多分支向不同的方向进行优化,这是重参化时性能提高的关键。除了对性能的影响外,线性缩放层还可以在训练过程中进行合并,使在线重参化成为可能。
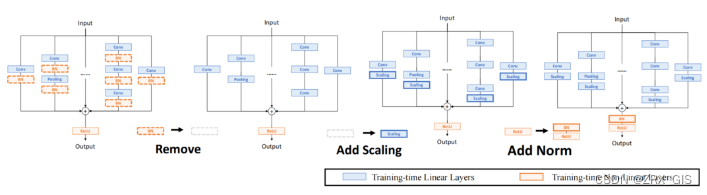
基于线性缩放层,作者修改了重参化块,具体来说,块的线性化阶段由以下3个步骤组成:首先,删除了所有的非线性层,即重参化块中的BN层;其次,为了保持优化的多样性,在每个分支的末尾添加了一个缩放层,这是BN的线性替代方法;最后,为了稳定训练过程,在所有分支的添加后添加一个BN层。一旦完成线性化阶段,在重参化块中只存在线性层,这意味着可以在训练阶段合并块中的所有组件。
Block Squeezing
Block Squeezing步骤将计算和内存昂贵的中间特征映射上的操作转换为更经济的kernel上的操作。这意味着在计算和内存方面从减少到,其中、是特征图和卷积核的空间尺寸。一般来说,无论线性重参化块是多么复杂,以下2个属性始终成立:Block中的所有线性层,例如深度卷积、平均池化和所提出的线性缩放,都可以用带有相应参数的退化卷积层来表示;Block可以由一系列并行分支表示,每个分支由一系列卷积层组成。
有了上述两个特性,如果可以将多层(即顺序结构)、多分支(即并行结构)简化为单一卷积,就可以压缩一个块。
多分支拓扑结构的梯度分析
结论是,对于去掉BN层的分支,利用缩放层可以使其优化方向多样化,并防止其退化为单一的优化方向。