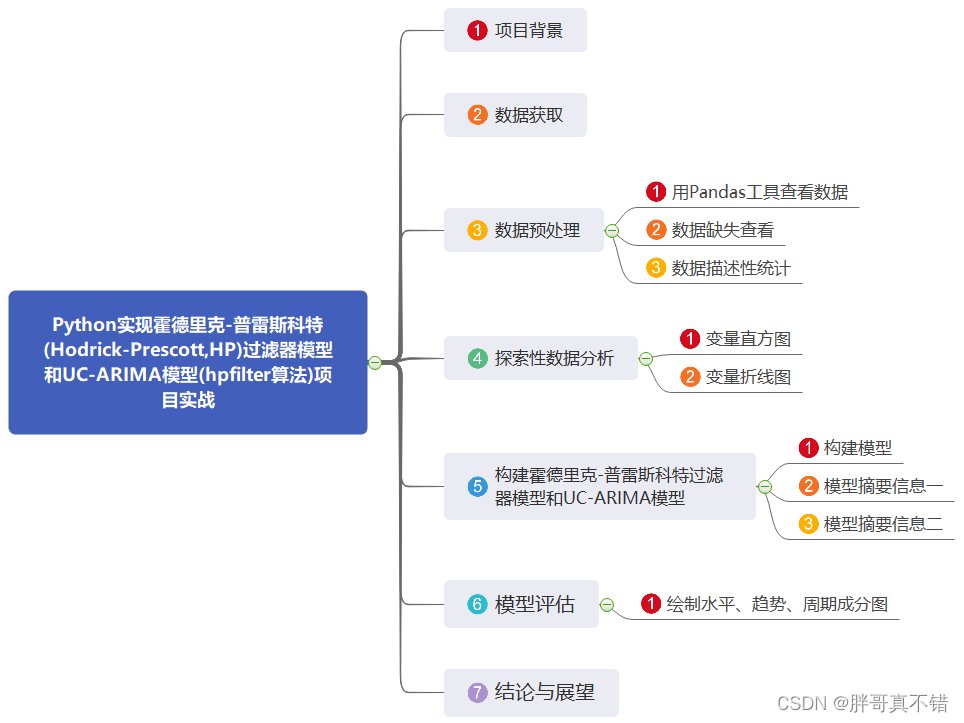
说明：这是一个机器学习实战项目（附带数据+代码+文档+视频讲解），如需数据+代码+文档+视频讲解可以直接到文章最后获取。

1.项目背景

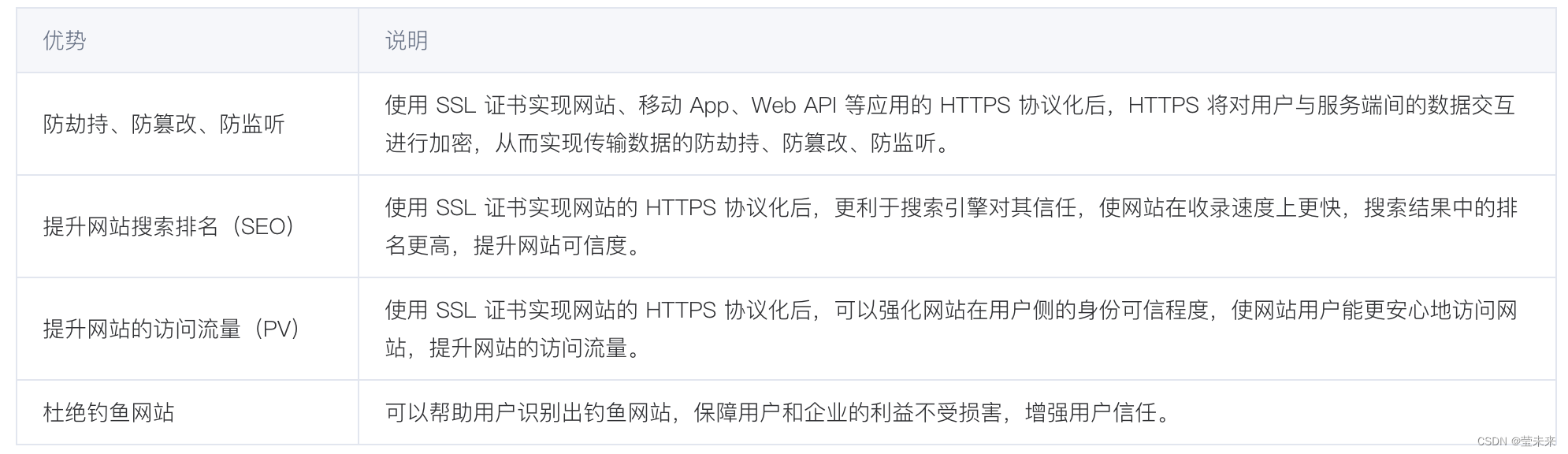
霍德里克-普雷斯科特（Hodrick-Prescott, HP）过滤器模型： HP滤波器是一种用于时间序列分析中的数据分解方法，由经济学家艾伦·霍德里克和爱德华·普雷斯科特在1980年代提出。该滤波器主要用于分离经济时间序列中的长期趋势部分与短期波动或周期性成分。它通过最小化一个加权的平方误差函数来实现这一目标，其中误差项是趋势和实际观测值之间的差值，并且误差项的平方和被乘以一个常数λ（Lambda），这个参数的选择可以根据数据的时间频率进行调整。通常情况下，HP滤波器对于季度数据选择较大的λ值，年度数据选择较小的λ值。

hpfilter算法一般指的是实施霍德里克-普雷斯科特滤波器的具体计算过程，而UC-ARIMA模型则可能表示一种结合了未观测组件模型（UCM）的某些思想以及ARIMA模型的技术来进行时间序列分析的方法论框架。

本项目通过hpfilter和UnobservedComponents算法来构建霍德里克-普雷斯科特(Hodrick-Prescott,HP)过滤器模型和UC-ARIMA模型。       

2.数据获取

本次建模数据来源于网络(本项目撰写人整理而成)，数据项统计如下：

编号	变量名称	描述
1	DATE	日期
2	UNRATE	失业率

数据详情如下(部分展示)：

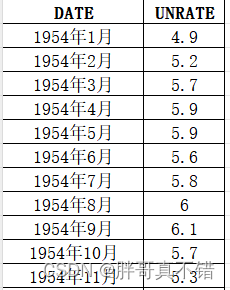
3.数据预处理

3.1 用Pandas工具查看数据

使用Pandas工具的head()方法查看前五行数据：

关键代码：

3.2 数据缺失查看

使用Pandas工具的info()方法查看数据信息：

      

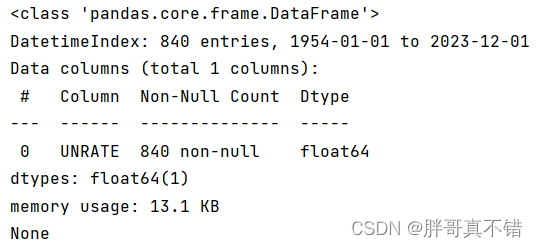
从上图可以看到，总共有1个变量，数据中无缺失值，共840条数据。

关键代码： 

3.3 数据描述性统计

通过Pandas工具的describe()方法来查看数据的平均值、标准差、最小值、分位数、最大值。 

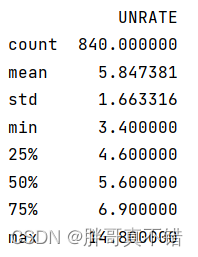
关键代码如下：    

4.探索性数据分析

4.1 变量直方图

用Matplotlib工具的hist()方法绘制直方图：

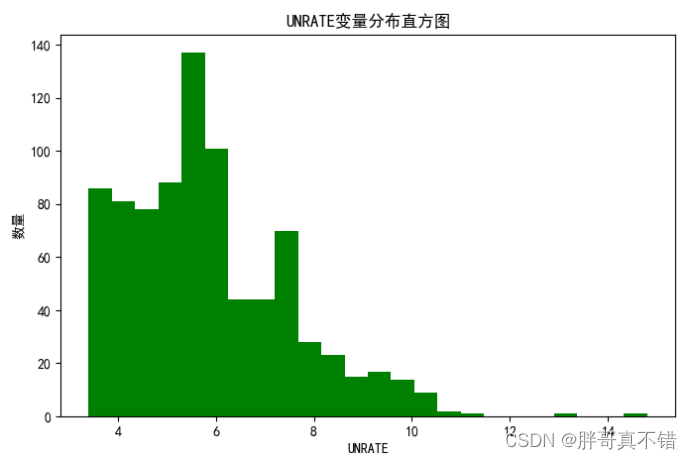
从上图可以看到，变量主要集中在4~10之间。  

4.2 变量折线图

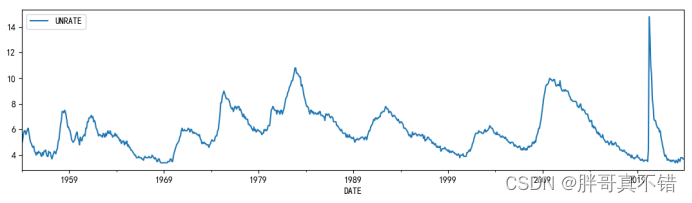
5.构建霍德里克-普雷斯科特过滤器模型和UC-ARIMA模型

主要使用hpfilter和UnobservedComponents算法，用于霍德里克-普雷斯科特过滤器模型和UC-ARIMA模型。    

5.1 构建模型

编号	模型名称	参数
1	霍德里克-普雷斯科特过滤器模型和UC-ARIMA模型	lamb=129600
2		'rwalk'
3		autoregressive=4

5.2 模型摘要信息一

模型中的趋势部分为随机游走，在模型中加入一个AR(4)过程：

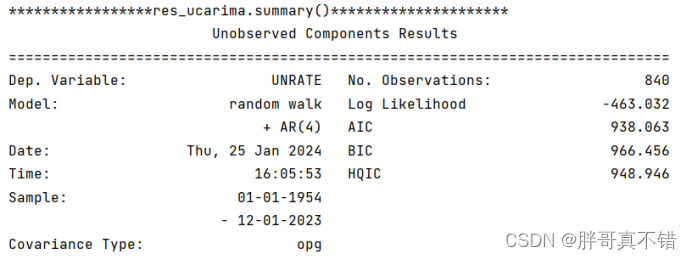
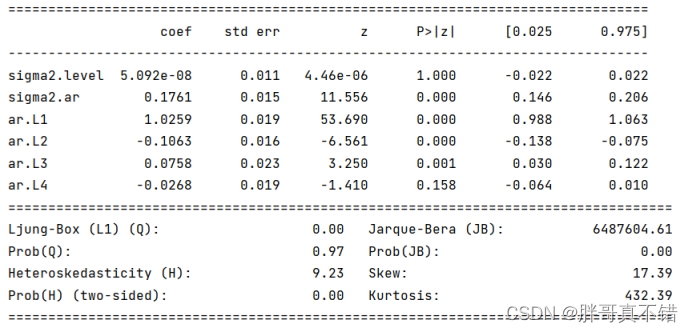
5.3 模型摘要信息二

具有随机游走趋势、阻尼周期性波动和随机成分的时间序列模型：

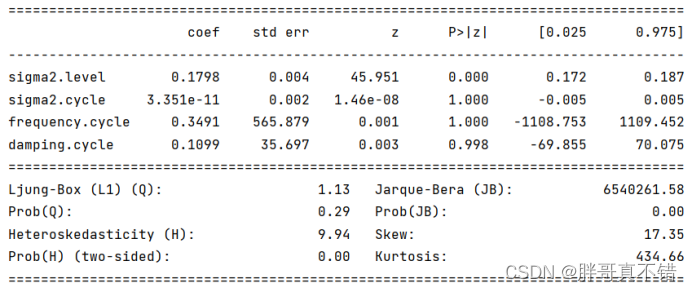
6.模型评估

6.1 绘制水平、趋势、周期成分图

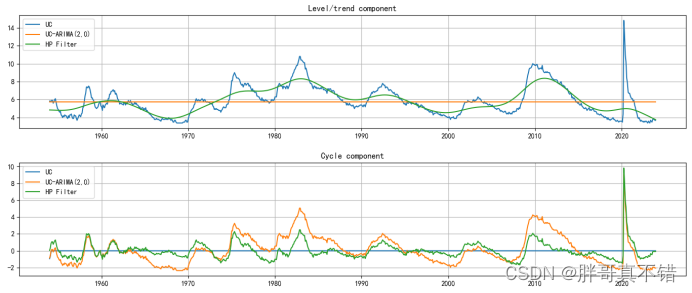
7.结论与展望

综上所述，本文采用了hpfilter和UnobservedComponents算法来构建霍德里克-普雷斯科特过滤器模型和UC-ARIMA模型，最终证明了我们提出的模型效果良好。此模型可用于日常产品的预测。

# 本次机器学习项目实战所需的资料，项目资源如下：
 
# 项目说明：
 
# 获取方式一：
 
# 项目实战合集导航：
 
https://docs.qq.com/sheet/DTVd0Y2NNQUlWcmd6?tab=BB08J2
 
# 获取方式二：

链接：https://pan.baidu.com/s/1J_jtYSZDCziaX9fanrjcCA 
提取码：ujif