这里写目录标题
- 一、81. 搜索旋转排序数组 II
- 二、167. 两数之和 II - 输入有序数组
- 三、441. 排列硬币
- 四、374. 猜数字大小
- 五、367. 有效的完全平方数
- 六、69. x 的平方根
一、81. 搜索旋转排序数组 II
中等
已知存在一个按非降序排列的整数数组 nums ,数组中的值不必互不相同。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转 ,使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。
给你 旋转后 的数组 nums 和一个整数 target ,请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ,则返回 true ,否则返回 false 。
你必须尽可能减少整个操作步骤。
示例 1:
输入:nums = [2,5,6,0,0,1,2], target = 0
输出:true
示例 2:
输入:nums = [2,5,6,0,0,1,2], target = 3
输出:false
class S81:
def func(self, nums, target):
left = 0
right = len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return True
elif nums[mid] > nums[right]:
if nums[mid] > target and target >= nums[left]:
right = mid - 1
else:
left = mid + 1
elif nums[mid] <= nums[right]:
if nums[mid] < target and target <= nums[right]:
left = mid + 1
else:
right = mid - 1
return False
r = S81()
nums = [2, 5, 6, 0, 0, 1, 2]
target = 3
print(r.func(nums, target))
二、167. 两数之和 II - 输入有序数组
中等
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
示例 1:
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
示例 2:
输入:numbers = [2,3,4], target = 6
输出:[1,3]
解释:2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。
示例 3:
输入:numbers = [-1,0], target = -1
输出:[1,2]
解释:-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
def func1(nums, target):
left = 0
right = len(nums) - 1
while left < right:
if nums[left] + nums[right] == target:
return [left + 1, right + 1]
elif nums[left] + nums[right] > target:
right -= 1
else:
left += 1
return [-1, -1]
nums = [-1, 0]
target = -1
print(func1(nums=nums, target=target))
三、441. 排列硬币
简单
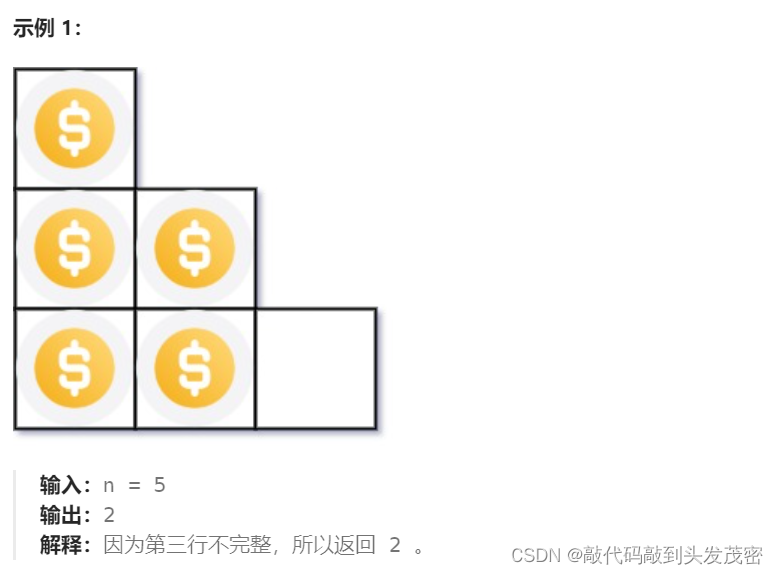
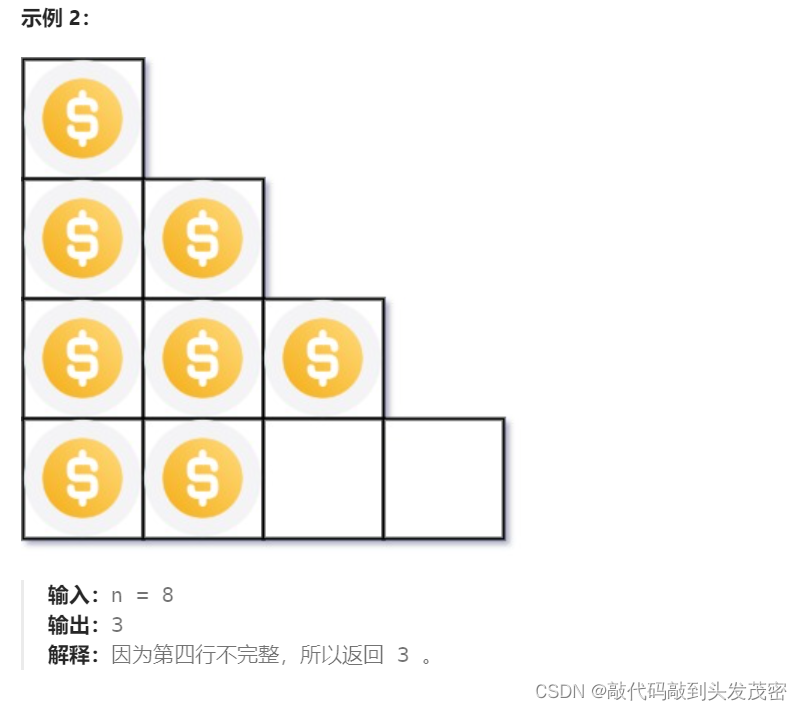
你总共有 n 枚硬币,并计划将它们按阶梯状排列。对于一个由 k 行组成的阶梯,其第 i 行必须正好有 i 枚硬币。阶梯的最后一行 可能 是不完整的。
给你一个数字 n ,计算并返回可形成 完整阶梯行 的总行数。
解题思路
1.二分查找,设立左右边界分别为1和n,每次取中间值mid为行数,将mid行总数和n对比
3.在不断的判定后如果硬币不能刚好分完,那么left会等于能分的最多行数+1,right会等于总量超出n的最小行数-1,即为能分的最多行数,
class S441:
def func(self,n):
left=1
right=n
while left<=right:
mid=(left+right)//2
if (1+mid)*mid//2<=n:
left=mid+1
else:
right=mid-1
return right
r=S441()
n=5
print(r.func(n))
四、374. 猜数字大小
简单
猜数字游戏的规则如下:
每轮游戏,我都会从 1 到 n 随机选择一个数字。 请你猜选出的是哪个数字。
如果你猜错了,我会告诉你,你猜测的数字比我选出的数字是大了还是小了。
你可以通过调用一个预先定义好的接口 int guess(int num) 来获取猜测结果,返回值一共有 3 种可能的情况(-1,1 或 0):
-1:我选出的数字比你猜的数字小 pick < num
1:我选出的数字比你猜的数字大 pick > num
0:我选出的数字和你猜的数字一样。恭喜!你猜对了!pick == num
返回我选出的数字。
示例 1:
输入:n = 10, pick = 6
输出:6
示例 2:
输入:n = 1, pick = 1
输出:1
示例 3:
输入:n = 2, pick = 1
输出:1
示例 4:
输入:n = 2, pick = 2
输出:2
调用预定义的接口guess来得到高了还是低了的信息,数字 范围是[1,n][1,n][1,n],直到猜中题目pick的数字。
运用二分查找,从范围[1,n][1,n][1,n]开始,不断的折半,调用guessguessguess,如果midmidmid高了,就往左半折,如果低了就往右半折,直到找到了
class S374:
def func(self,n):
start=1
end=n
while start<=end:
mid=(start+end)//2
ret=guess(mid)
if ret==0:
return mid
elif ret==1:
start=mid+1
else:
end=mid-1
r=S374()
n=10
print(r.func(n))
五、367. 有效的完全平方数
简单
给你一个正整数 num 。如果 num 是一个完全平方数,则返回 true ,否则返回 false 。
完全平方数 是一个可以写成某个整数的平方的整数。换句话说,它可以写成某个整数和自身的乘积。
不能使用任何内置的库函数,如 sqrt 。
示例 1:
输入:num = 16
输出:true
解释:返回 true ,因为 4 * 4 = 16 且 4 是一个整数。
示例 2:
输入:num = 14
输出:false
解释:返回 false ,因为 3.742 * 3.742 = 14 但 3.742 不是一个整数。
class S367:
def func(self,num):
l=1
r=num
while l<=r:
mid=(l+r)//2
if mid*mid==num:
return True
elif mid*mid>num:
r=mid-1
else:
l=mid+1
return False
r=S367()
num=14
print(r.func(num))
六、69. x 的平方根
简单
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4
输出:2
示例 2
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842…, 由于返回类型是整数,小数部分将被舍去。
思路:二分查找
class S69:
def func(self,x):
left=0
right=x #任何数的平方根都小于本身
ans=1
while left<=right:
mid=(left+right)//2
if mid*mid==x:
return mid
elif mid*mid<x:
ans=mid
left=mid+1
else:
right=mid-1
return ans
r=S69()
x=12
print(r.func(x))