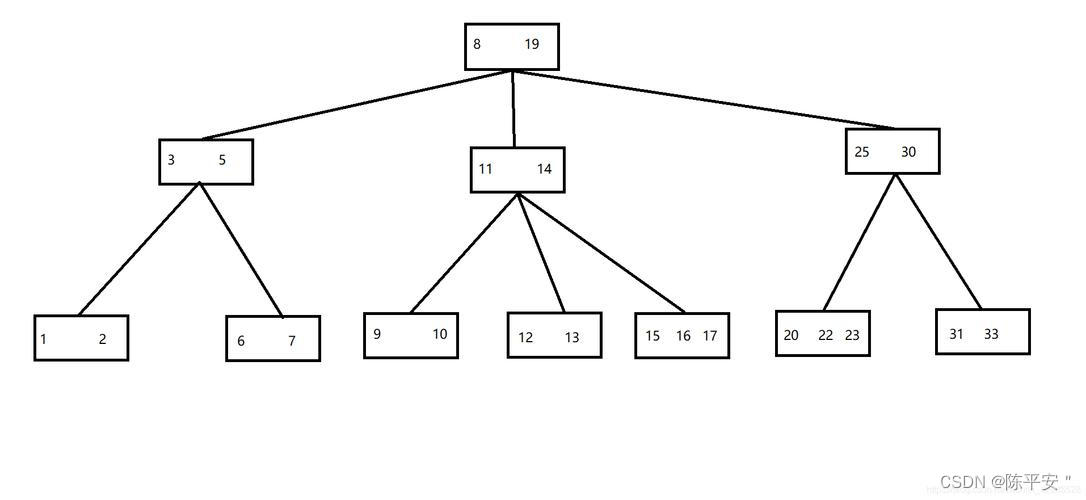
1.哈夫曼树

在哈夫曼树中,每个非叶子节点都有两个子节点(因为哈夫曼树是一种二叉树),而叶子节点没有子节点。如果用二叉链表作为存储结构,每个节点需要包含两个指针域,分别指向其左孩子和右孩子。因此,在哈夫曼树中总共有 2m 个指针域。
2.循环队列知识点
1.队列尾指针前进: Q.rear=(Q.rear+1)%MaxSize;
2.队列长度:(Q.rear-R.front+MaxSize)%MaxSize;
3.循环队列判断空的条件:Q.front=Q.rear;
4.判断队列是否为满:(Q.rear+1)%MaxSize=Q.front;
2.1入队:
bool enQueue(sQueue &queue,ElemType x){
//1.首先判断队列是否为满
if((queue.rear+1)%MaxSize==queue.front) return false; //(Q.rear+1)%MaxSize==Q.front;
//2.添加入队列
queue.data[queue.rear]=x;
queue.rear=(queue.rear+1)%MaxSize;
return true;
}
2.2出队:
//首先判断是否为空,若不为空,将队列front元素pop
bool Dequeue(Queue &queue,ElemType &x){
//1.判断队列中是否存在元素
if(queue.rear==queue.front) return false;
//2.将头指针元素赋值x
x=queue.data[queue.front];
//3.头指针前进(因为front指向的元素已被pop)
queue.front=(queue.front+1)%MaxSize;
return true;
}
补:链式队列
1.判断队列是否为空的条件:
if(queue.front==NULL&&queue.rear==NULL)
2.链式入队:
void enQueue(LinkQueue &queue,ElemType x){
//1.首先创建节点,并将其赋值
LinkNode* newNode=(LinkNode*)malloc(sizeof(LinkNode));
newNode->data=x;
//2.连上尾指针
queue.rear->next=newNode;//连上尾指针:queue.rear->next=newNode
queue.rear=newNode; //更新尾指针
}
3.链式出队:
bool DeQueue(LinkQueue &queue,ElemType &x){
//1.判断队列是否为空
if(queue.front==NULL&&queue.rear==NULL) return false; //在循环队列中判断队列是否为空的条件是:queue.front==queue.rear
//2.出队:首先用一个临时节点继承queue.front——>2.然后更新queue.front,使其指向临时节点的下一个节点——>3.最后free掉当前的临时节点
LinkNode *cur=queue,front;
queue.front=cur.next;
free(cur);
return true;
}
LinkNode*cur=queue.front;
queue.front=cur.next;
free(cur);
3.前中后序遍历
老办法,先找根节点,然后根据提供的两种遍历方式->确定树的结构

4.完全图,连通图
完全无向图:n个顶点有n*(n-1)/2条边
完全有向图:n个顶点有n*(n-1)条边
连通图:至少有n-1条边
完全连通图一定是有向图,但反之不一定,因为并不是每个顶点到其他顶点都有边的
邻接表的表头节点的个数与顶点个数相关
邻接表的每个节点的连接个数:与图中当前节点相连的边数相关
5.二叉树的最小高度
直接夹逼算即可,比如2000个节点,2^11-1>2000,2的十次方-1代表高度为10的树的最大节点数<2000,所以最小高度为11

6.快排的思路:
1.首先是确定基准元素privot——>2.然后进行分区操作,大于privot的在右边,小于privot的在左边(按比较次序进行排序)——>3.分区后,递归当前基准元素的左右侧分区(重复1,2操作)
[7, 2, 9, 1, 6, 8, 5, 3] 进行排序。


7.HASH查找技术
1.键是如何映射到哈希表中的位置——哈希函数的设计
2.不同键映射到相同位置——如何解决哈希冲突的方法
为了能有效地应用HASH查找技术,必须解决的两个问题是哈希函数的设计和处理哈希冲突的方法。哈希函数的设计决定了如何将键映射到哈希表中的位置,而处理哈希冲突的方法则确定了当不同键映射到相同位置时如何进行处理,以确保数据的准确性和高效的查找操作。
8.栈的操作
8.1进栈:
typedef struct{
int s[100]; //栈存储元素的地方
int top; //顶点指针
}sqStack;
void push(sqStack &stack,int x){ //元素x进栈
if(stack.top==m-1) printf("overflow"); //满溢出
else {
stack.s[stack.top]=x;
stack.top++;
}
}
8.2判断栈为空的条件,栈满条件
stack.top==-1;
stack.top==MaxSize-1;
8.3出栈操作:
bool pop(Stack &stack,ElemType &x){
//1.首先判断栈是否为空
if(stack.top==-1) return false;
//2.若不为空,将栈顶元素赋值,且stack.top--
x=stack.data[stack.top--];
return true;
}
8.4进栈操作:
bool push(Stack &stack,int x){
//1.首先判断栈是否满了
if(stack.top==MaxSize-1) return false;
//2.入栈操作;将x元素赋值给stack.data[stack.top++]=x
stack.data[stack.top++]=x;
return true;
}
8.4栈的注意事项:
1.另外,注意栈只能确定入栈次序,但是并不能确定出栈次序,还需根据栈的容量来具体分析
2.三个不同元素进栈,能够得到6种不同的出栈序列(选中第一个有三种可能,剩下有两个位置,3*2)
9.树的空指针域
为:n0的空指针个数2+n11
10.无向图的常见性质
无向图中,所有顶点的度数之和=边的数量的两倍,所以若顶点度数之和为d,那么边数e=d/2
11.初始堆
1.先按照顺序,变成一颗完全二叉树——>2.然后从叶子节点开始,自下而上,调整堆(根父节点相比,一步步调整上去)
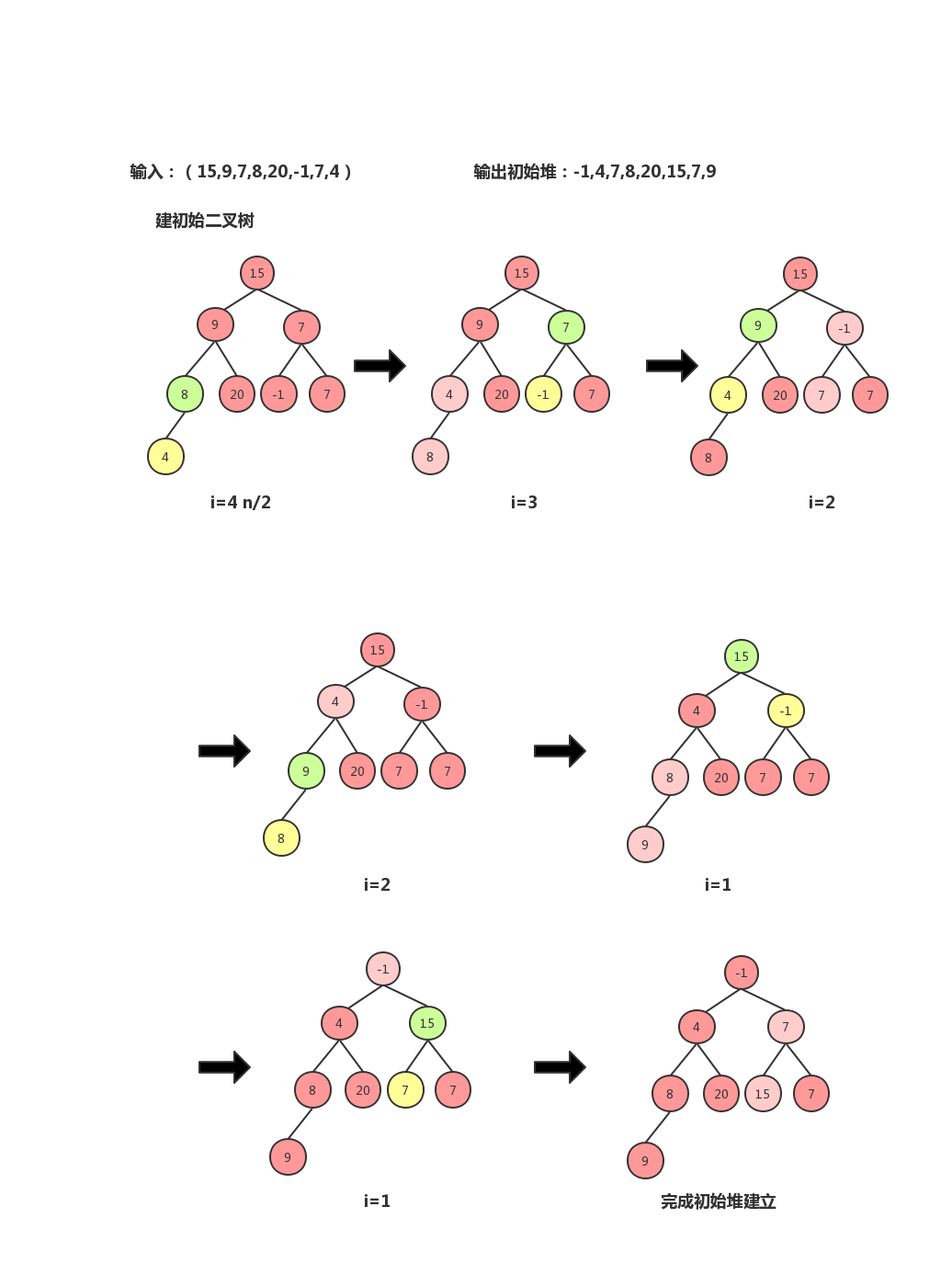
for(int i=n/2;i>0;i--){
par = i;//父节点
while(par*2<=n){
lch = par*2;//左子节点
rch = lch+1;//右子节点
min = lch;
if(rch<=n){//有两个子节点
if(arr[lch]>arr[rch]){
min = rch;
}
}
if(arr[min]<arr[par]){
swap(arr,min,par);
par = min; //往下遍历
}
}
}
插入法:将n个记录依次插入二叉树中,若其比父节点值小,则浮操作,直到其比父节点大