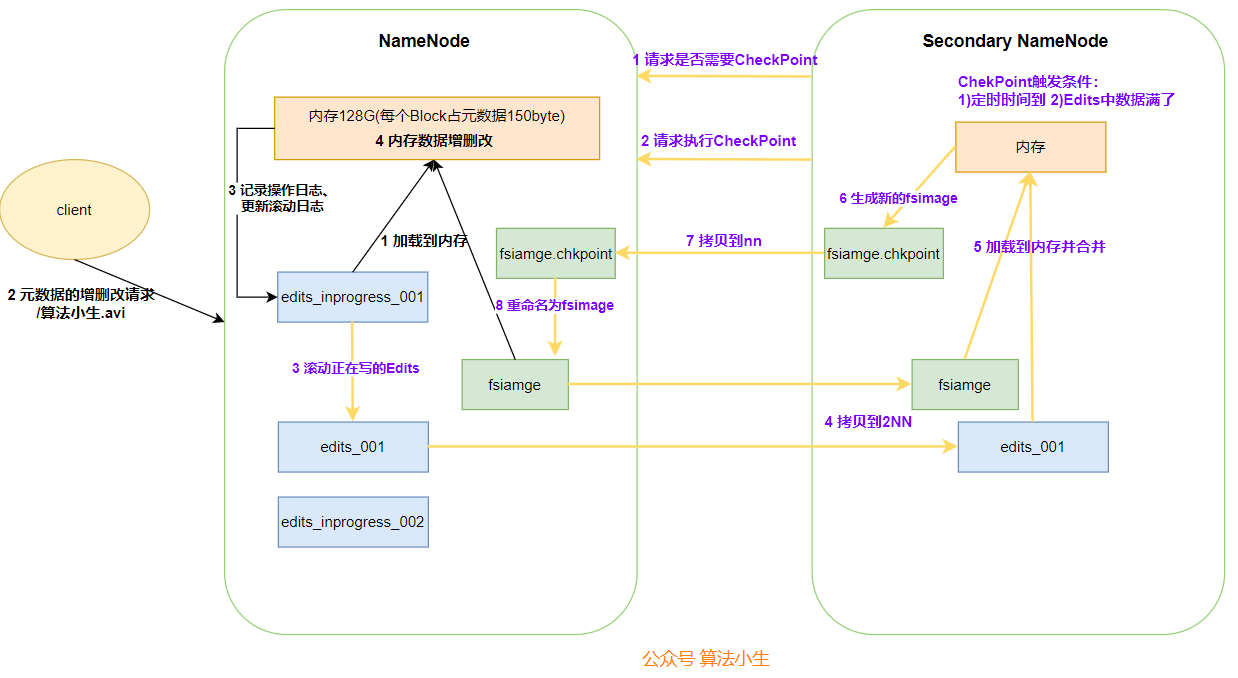
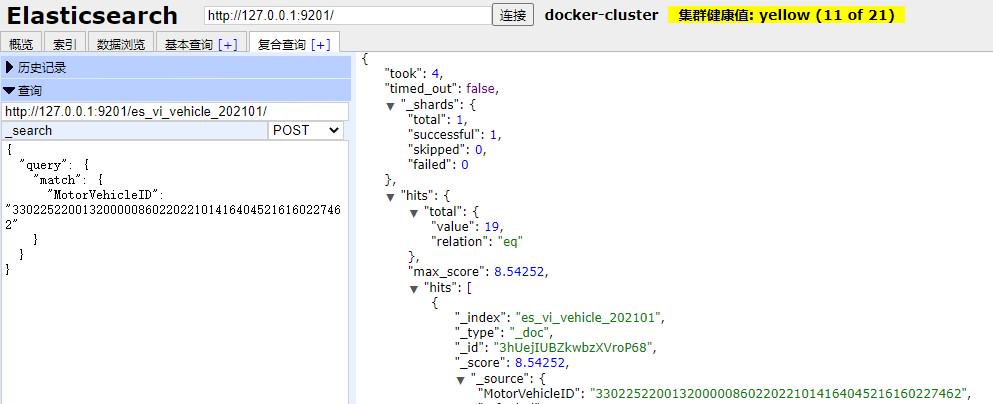
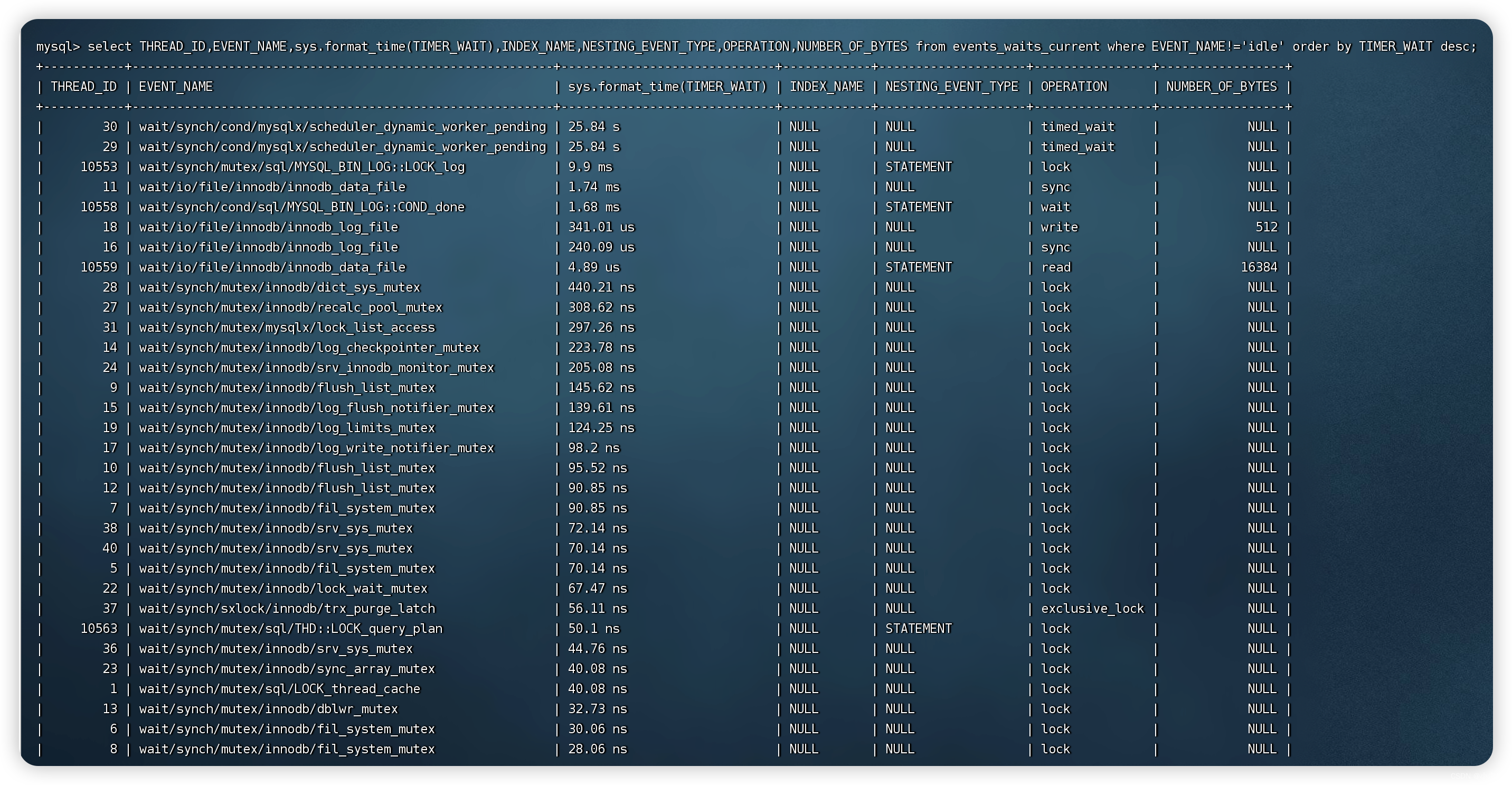
MATLAB中可以用来求解常微分方程(组)的函数有ode23、 ode23s、 ode23t、 ode23tb 、ode45、ode15s和odel13等,见下表。它们的具体调用方法类似,为了方便后面的描述,
在后面的介绍中将使用solver统一代替它们。

函数的具体调用方法如下。
[T,Y] =solver( odefun, tspan,y0)
[T,Y] = solver( odefun,tspan, y0,options)
[T,Y]=soIver( odefun, tspan,yO,options,pl ,p2,...)
在区间tspan=[t0,tf].上,使用初始条件y0,求解常微分方程y'=f(t,y)。其中解向量Y中的每行结果对应于时间向量T中的每个时间点。利用传递给函数odefun的p1, p2, .参数进行求解。solver 函数中涉及的参数见表。

odeset函数的用法与optimset函数类似,利用所设置的可选参数进行求解,solver 中options的参数见表。


MATLAB可以求解3种类型一阶常微分方程,即显式常微分方程、线性隐式常微分方程和完全隐式常微分方程。
显式常微分方程
显式常微分方程的形式为
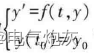
例:显式常微分方程求解实例。
已知微分方程为y"-u(1-y^2)y'+y=0 (y(0)=0,y'(0)=2;t∈[0,30]),分别取μ=3和μ=5求解该方程。
首先对微分方程进行变换得到形式为

然后对方程组进行函数描述,并保存为myfun6. 9. m,其内容如下所示。
function output = myfun6.9(t,y ,mu)
output = zeros(2,1);
output(1)=y(2);
output(2)= mu*(1-y(1)^2) *y(2)-y(1);
对方程组进行求解,在命令行窗口中输入如下语句。
>>[t1,y1] =ode45( @ myfun6_ 9,[0 30],[0;2],[],3); %mu=3
[t2,y2]=ode45(@ myfun6 9,[0 30],[0;2],[],5); %mu=5
plot(t1,y1(:,1),'-',t2,y2(:,2),'--')
title( '显式常微分方程的解');
xlabel('t');
ylabel('y ');
legend( 'mu=3',' mu=5');
图形窗口中的输出结果如图所示。

线性隐式常微分方程
线性隐式常微分方程的形式为

例:线性隐式常微分方程求解实例。
已知微分方程(ty^2+1)y'=3y"+y+4(t∈[0,10];y(0)=2),求解该方程。
首先根据微分方程(ty^2+1)y'=3y^3 +y+4和通式4M(1,y)y'=f(t,y),得到:

然后对f(1,y)进行函数描述,并保存为myfun6_ 10f. m,其内容如下所示。
function output= myfun6_ 10f(t,y)
output=3* y. ^3+y+4;
对M(t,y)进行函数描述,并保存为myfun6_ 10M. m,其内容如下所示。
function output = myfun6_10M(t,y)
output=t*y. ^2+1;
最后对方程进行求解,在命令行窗口中输人如下语句。.
>>options = odeset( ' RelTol ',le-6, 'OutputFen ',' odeplot ',' Mass ' ,@ myfun6_ 10M);
[t,y] = ode45( @ myfun6_ 10f,[0 10] ,2 ,options);
xlabel('t');
ylabel('y ');
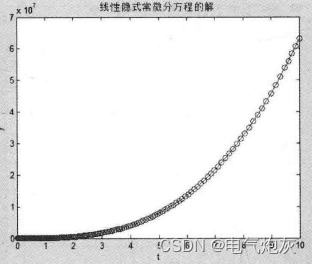
title( '线性隐式常微分方程的解')
图形窗口中的输出结果如图所示。
完全隐式常微分方程
完全隐式常微分方程的形式为:

例:完全隐式常微分方程求解实例。
已知方程如下求解该方程。

首先对方程进行函数描述,并保存为myfun6_ 11. m,其内容如下所示。
function output = myfun6_ 11(t,y ,dydt)
output=t*y. ^2*dydt. ^3-2* y.^3*dydt. ^2+3*t*(t^2+1) *dydt -t^2*y;
其次对方程进行求解,在命令行窗口中输人如下语句。
>>t0=1;
y0=sqrt(3/2);
yp0=0;
[y0,yp0] =decie( @ myfun6_ 11 ,t0,y0,1 ,yp0,0) ;
[t,y]=ode15i( @ myfun6 11,[1 20] ,y0,yp0);
plot(t,y);
xlabel('t');
ylabel('y');
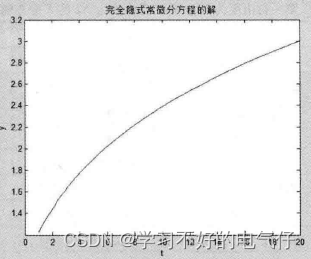
title(完全隐式常微分方程的解');
图形窗口中的输出结果如图所示。